この記事では、「数学的帰納法」を使った証明問題の解き方をできるだけわかりやすく解説していきます。
等式の証明、不等式の証明、整数の性質の証明、数列・漸化式の証明など、数学的帰納法を使う問題パターンをまとめて説明していきますので、この記事を通してぜひマスターしてくださいね!
目次
数学的帰納法とは?
数学的帰納法とは、ある命題がすべての自然数において成り立つことを帰納的に証明する方法です。
【証明したいこと】
自然数 \(n\) に対する命題 \(P\) がすべての自然数 \(n\) について成り立つ。
【証明手順】
以下が成り立つことを示せば、すべての \(n\) について成り立つといえる。
[1] \(n = 1\) のとき \(P\) が成り立つ。
[2] \(n = k\)(\(k\) は自然数)のとき \(P\) が成り立つと仮定すると、\(n = k + 1\) のときにも \(P\) が成り立つ。
数学的帰納法のイメージはドミノ倒しです。
初めの \(1\) つが正しい [1]、そして \(1\) つ手前が正しいならその次も正しい [2] ことが示せれば、すべて正しいことが順番に示されていくのです。
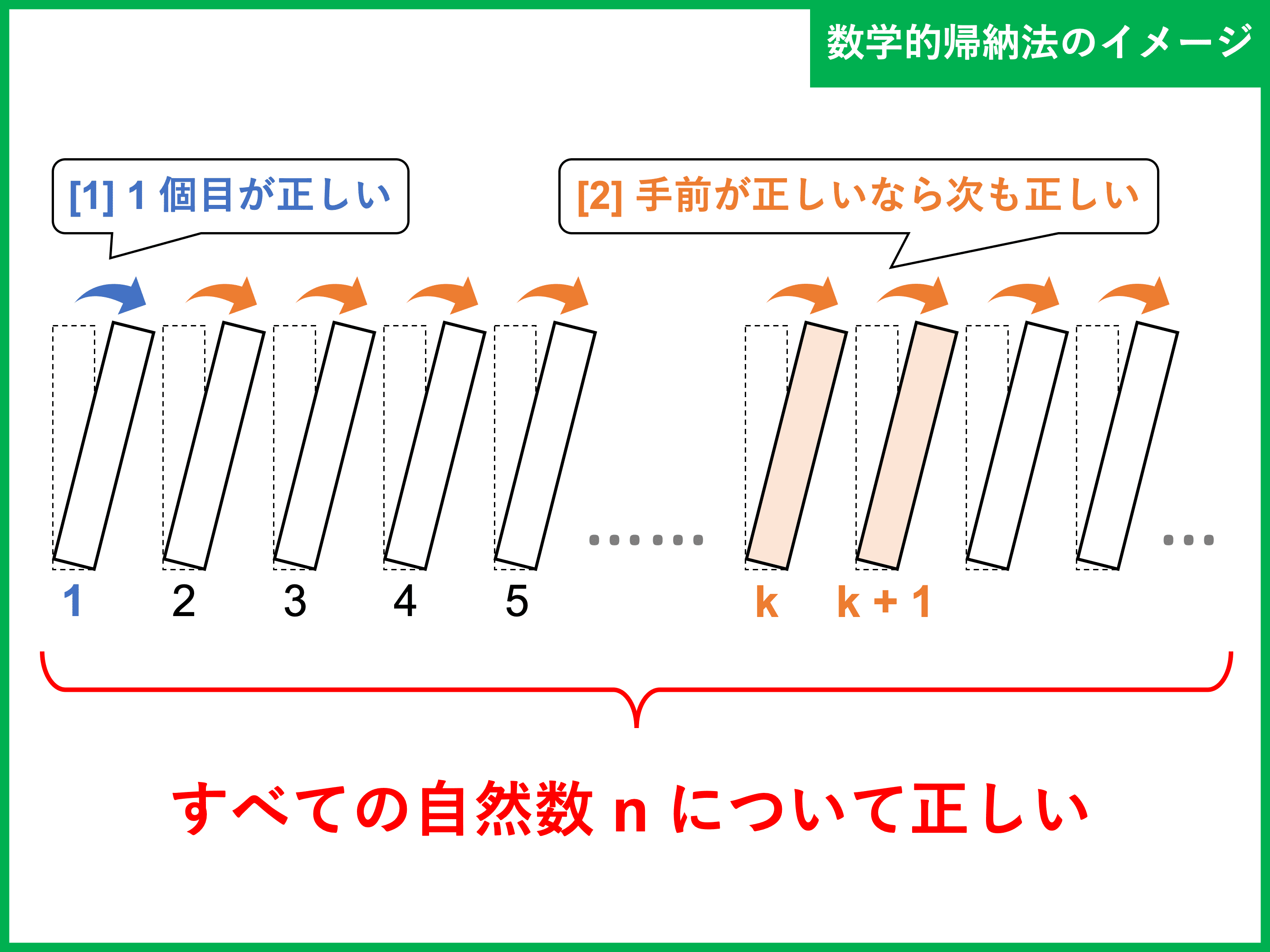
数学的帰納法による証明の流れは上記 [1] [2] と決まっているので、慣れてしまえば簡単に活用できるようになります。
【参考】帰納法と演繹法
「帰納」とは、個別の事実から共通の性質を取り出し、一般的な命題・法則を導くことを言います。
反対に、一般的・普遍的な命題・法則からより個別・特殊な結論を導くことを「演繹」と言います。

命題とは、正しいか正しくないかが明確に決まる文章や数式のことです。
 命題とは?数学用語(対偶、逆、裏、真偽)の意味や証明問題
命題とは?数学用語(対偶、逆、裏、真偽)の意味や証明問題
数学的帰納法の証明手順
数学的帰納法による証明の書き方を、手順を追ってていねいに説明します。
すべての自然数 \(n\) について、次の等式が成り立つことを証明せよ。
\(2 + 4 + 6 + \cdots + 2n = n(n + 1)\)
まずは、証明したい命題(数式)に番号を振っておきます。
こうすることで、証明中に長々とした数式を何度も書かなくて済みます。
\(2 + 4 + 6 + \cdots + 2n = n(n + 1)\) …①
とする。
示したい命題(数式)が、\(n = 1\) のときに成り立つことを示します。
この工程を [1] とします。
\(\text{(左辺)} = 2\)
\(\text{(右辺)} = 1 \cdot 2 = 2\)
よって、①は成り立つ。
ここで、\(n\) が任意の自然数 \(k\) であるときに命題①が成り立つと仮定し、この式にも番号を振ります。
この STEP.3 と次の STEP.4 を合わせて工程 [2] とします。
①が成り立つと仮定すると、
\(2 + 4 + 6 + \cdots + 2k = k(k + 1)\) …②
STEP.3 の仮定のもとで、\(n = k + 1\) のときにも命題①が成り立つことを示します。
つまり、例題においてこのとき示したいのは、\(2 + 4 + 6 + \cdots + 2k + 2(k + 1) = (k + 1)(k + 2)\) という等式です。
この左辺を、仮定の式②を使って変形し、本当に右辺の形になることを導きます。
\(n = k + 1\) のときを考えると、②から
\(\color{salmon}{2 + 4 + 6 + \cdots + 2k} + 2(k + 1)\)
\(= \color{salmon}{k(k + 1)} + 2(k + 1)\)(②を利用)
\(= (k + 1)(k + 2)\)
よって、\(n = k + 1\) のときも①は成り立つ。
このことを明記すれば、証明完了です。
\(2 + 4 + 6 + \cdots + 2n = n(n + 1)\) …①
とする。
[1] \(n = 1\) のとき
\(\text{(左辺)} = 2\)
\(\text{(右辺)} = 1 \cdot 2 = 2\)
よって、①は成り立つ。
[2] \(n = k\) のとき
①が成り立つと仮定すると、
\(2 + 4 + 6 + \cdots + 2k = k(k + 1)\) …②
\(n = k + 1\) のときを考えると、②から
\(\text{(左辺)}\)
\(= 2 + 4 + 6 + \cdots + 2k + 2(k + 1)\)
\(= k(k + 1) + 2(k + 1)\)
\(= (k + 1)(k + 2)\)
よって、\(n = k + 1\) のときも①は成り立つ。
[1], [2] から、すべての自然数 \(n\) について①は成り立つ。
(証明終わり)
数学的帰納法による証明手順は、どんな問題であっても基本的には共通です。
定型文として覚えておきましょう!
数学的帰納法が使える問題パターン
数学的帰納法が使える問題は、ズバリ「任意の自然数 \(n\)」を含む証明問題です。
「すべての自然数 \(n\) について」という表現があったら、「数学的帰納法を使うかも?」とアンテナを立ててください。
証明対象としては、大きく分けて以下の \(4\) パターンがあります。
- 等式の証明
例:「等式 \(◯ = △\) が成り立つことを示せ」 - 不等式の証明
例:「不等式 \(◯ > △\) が成り立つことを示せ」 - 整数の性質の証明
例:「〜が〇の倍数であることを示せ」「〜の余りが〇であることを示せ」「〜が〇で割り切れることを示せ」 - 数列・漸化式の証明
例:「一般項 \(a_n\) を推測し、その推測が正しいことを数学的帰納法で示せ」
以降、それぞれの問題の解き方を説明します。
① 数学的帰納法による等式の証明
次の例題を通して、数学的帰納法による等式の証明について説明します。
すべての自然数 \(n\) について、次の等式が成り立つことを証明せよ。
\(\displaystyle 1^3 + 2^3 + \cdots + n^3 = \frac{1}{4} n^2(n + 1)^2\)
[2] で正しいと仮定する \(n = k\) における等式を、\(n = k + 1\) のときにうまく利用するのがポイントです。
\(n = k + 1\) のときに示すべき等式をイメージしておいて、どう式変形したらそこへたどり着けるかを考えます。
\(\displaystyle 1^3 + 2^3 + \cdots + n^3 = \frac{1}{4} n^2(n + 1)^2\) …①
とする。
[1] \(n = 1\) のとき
\(\text{(左辺)} = 1^3 = 1\)
\(\displaystyle \text{(右辺)} = \frac{1}{4} \cdot 1^2 \cdot 2^2 = 1\)
よって、①は成り立つ。
[2] \(n = k\) のとき
①が成り立つと仮定すると、
\(\displaystyle 1^3 + 2^3 + \cdots + k^3 = \frac{1}{4} k^2(k + 1)^2\) …②
\(n = k + 1\) のときを考えると、②から
\(1^3 + 2^3 + \cdots + k^3 + (k + 1)^3\)
\(\displaystyle = \frac{1}{4} k^2(k + 1)^2 + (k + 1)^3\)
\(\displaystyle = \frac{1}{4} (k + 1)^2 \{k^2 + 4(k + 1)\}\)
\(\displaystyle = \frac{1}{4} (k + 1)^2(k + 2)^2\)
よって、\(n = k + 1\) のときも①は成り立つ。
[1], [2] から、すべての自然数 \(n\) について①は成り立つ。
(証明終わり)
② 数学的帰納法による不等式の証明
次の例題を通して、数学的帰納法による不等式の証明について説明します。
\(n \geq 10\) のすべての自然数 \(n\) について、次の不等式を証明せよ。
\(2^n > 10n^2\)
不等式でも流れは同じで、\(n = k\) のときの不等式を利用して \(n = k + 1\) のときに \(\text{(左辺)} > \text{(右辺)}\) を示します。
自然数 \(n\) に条件があるときは、証明の開始地点に注意します。
通常「自然数 \(n\)」と言われれば「\(n = 1\)」から証明を開始しますが、今回は「\(n \geq 10\)」と条件があるので、「\(n = 10\)」から始めます。
このとき、[2] も合わせて「\(n = k\) \((k \geq 10)\) のとき」と \(k\) の範囲を指定する必要があるので、忘れないようにしましょう!
\(2^n > 10n^2\) …①
とする。
[1] \(n = 10\) のとき
\(\text{(左辺)} = 2^{10} = 1024\)
\(\text{(右辺)} = 10 \cdot 10^2 = 1000\)
よって、①は成り立つ。
[2] \(n = k\) \((k \geq 10)\) のとき
①が成り立つと仮定すると、
\(2^k > 10k^2\) …②
\(n = k + 1\) のとき、①の両辺の差を考えると、②から
\(2^{k + 1} − 10(k + 1)^2\)
\(= 2 \cdot 2^k − 10(k + 1)^2\)
\(> 2 \cdot 10k^2 − 10(k + 1)^2\)
\(= 10(k^2 − 2k − 1)\)
\(= 10\{(k − 1)^2 − 2\}\)
ここで、\(k \geq 10\) であるから、\(10\{(k − 1)^2 − 2\} > 0\)
ゆえに \(2^{k + 1} > 10(k + 1)^2\)
よって、\(n = k + 1\) のときも①は成り立つ。
[1], [2] から、\(n \geq 10\) のすべての自然数 \(n\) について①は成り立つ。
(証明終わり)
③ 数学的帰納法による整数の性質の証明
次の例題を通して、数学的帰納法による整数の性質の証明について説明します。
すべての自然数 \(n\) について、\(3^{3n} − 2^n\) は \(25\) の倍数であることを示せ。
示したい命題が数式でなくても、番号を振っておくと便利ですね。
また、「\(25\) の倍数であること」を任意の整数を使って数式として表現することがポイントです。
「\(3^{3n} − 2^n\) は \(25\) の倍数である」を①とする。
[1] \(n = 1\) のとき
\(3^{3 \cdot 1} − 2^1 = 27 − 2 = 25\)
よって、①は成り立つ。
[2] \(n = k\) のとき
①が成り立つと仮定すると、
\(3^{3k} − 2^k = 25m\) (\(m\) は整数) …②
とおける。
\(n = k + 1\) のときを考えると、②から
\(3^{3(k + 1)} − 2^{k + 1}\)
\(= 3^3 \cdot 3^{3k} − 2 \cdot 2^k\)
\(= 27(25m + 2^k) − 2 \cdot 2^k\)
\(= 27 \cdot 25m + (27 − 2)2^k\)
\(= 25(27m + 2^k)\)
\(27m + 2^k\) は整数であるから、\(3^{3(k + 1)} − 2^{k + 1} = 25(27m + 2^k)\) は \(25\) の倍数である。
よって、\(n = k + 1\) のときも①は成り立つ。
[1], [2] から、すべての自然数 \(n\) について①は成り立つ。
(証明終わり)
④ 数学的帰納法による数列・漸化式の証明
次の例題を通して、数学的帰納法による数列・漸化式の証明について説明します。
この分野では、「項間の関係式や漸化式から一般項を推測」→「数学的帰納法で証明」という流れで解かせる問題が非常に多いです。
\(4(a_1 + a_2 + \cdots + a_n) = (2n + 1)a_n + 1\) \((n = 1, 2, \cdots)\) で定まる数列 \(\{a_n\}\) がある。
(1) \(a_1, a_2, a_3\) を求めよ。
(2) 一般項 \(a_n\) を推測し、その推測が正しいことを数学的帰納法によって証明せよ。
(2) の証明部分では、問題文の等式と推測した一般項で \(n = k\) のときの等式の両方をうまく活用します。
\(4(a_1 + a_2 + \cdots + a_n) = (2n + 1)a_n + 1\) …①
とする。
(1)
①で \(n = 1\) とすると
\(4a_1 = 3a_1 + 1\)
よって
\(a_1 = 1\)
①で \(n = 2\) とすると
\(4(a_1 + a_2) = 5a_2 + 1\)
よって
\(a_2 = 4a_1 − 1 = 4 − 1 = 3\)
①で \(n = 3\) とすると
\(4(a_1 + a_2 + a_3) = 7a_3 + 1\)
よって
\(\begin{align}a_3 &= \frac{4(a_1 + a_2) − 1}{3} \\&= \frac{4(1 + 3) − 1}{3} \\&= 5\end{align}\)
答え: \(\color{red}{a_1 = 1, a_2 = 3, a_3 = 5}\)
(2)
(1) から、\(a_n = 2n − 1\) …② と推測できる。
一般項が②であることを数学的帰納法を用いて証明する。
[1] \(n = 1\) のとき
②で \(n = 1\) とすると
\(a_1 = 2 \cdot 1 − 1 = 1\)
(1) と一致するため、②は成り立つ。
[2] \(n = k\) のとき
②が成り立つと仮定すると、
\(a_k = 2k − 1\)
\(n = k + 1\) のときを考えると、①から
\(\{2(k + 1) + 1\} a_{k + 1} + 1\)
\(= 4(a_1 + a_2 + a_3 + \cdots + a_k + a_{k + 1})\)
\(= 4(a_1 + a_2 + a_3 + \cdots + a_k) + 4a_{k + 1}\)
\(= (2k + 1)a_k + 1 + 4a_{k + 1}\)
すなわち
\((2k + 3)a_{k + 1} = (2k + 1)a_k + 4a_{k + 1}\)
よって
\(\begin{align}(2k − 1)a_{k + 1} &= (2k + 1)a_k \\&= (2k + 1)(2k − 1)\end{align}\)
\(2k − 1 \neq 0\) より \(a_{k + 1} = 2k + 1 = 2(k + 1) −1\)
よって、\(n = k + 1\) のときも②は成り立つ。
[1], [2] から、すべての自然数 \(n\) について①は成り立つ。
(証明終わり)
以上で問題も終わりです。
数学的帰納法を使う問題はわりと特定しやすいので、証明プロセスさえ覚えておけば確実な得点源にできます。
さまざまな問題に取り組んで、数学的帰納法に慣れていってくださいね!
