この記事では、「オイラーの多面体定理」についてわかりやすく解説していきます。
定理の覚え方や証明方法、問題の解き方をていねいに説明していくので、ぜひこの記事を通してマスターしてくださいね!
目次
オイラーの多面体定理とは?
オイラーの多面体定理とは、多面体の頂点、辺、面の数について成り立つ以下の定理です。
凸多面体(へこみのない多面体)の頂点の数を \(v\)、辺の数を \(e\)、面の数を \(f\) とおくと、
\begin{align}\color{red}{v − e + f = 2}\end{align}
記号はそれぞれの英単語の頭文字からきています(頂点 Vertex、辺 Edge、面 Face)。
多面体とは、いくつかの多角形で囲まれた立体図形のことです。
円柱や球のように、曲面を含む立体図形は含まれないので注意しましょう。
いくつかの多面体を例に、頂点、辺、面の数を数えて定理が成り立つことを確認してみましょう。
(例1)直方体
頂点の数 \(v = 8\)、辺の数 \(e = 12\)、面の数 \(f = 6\) より、
\(\begin{align}v − e + f &= 8 − 12 + 6 \\&= 2\end{align}\)
(例2)三角柱
頂点の数 \(v = 6\)、辺の数 \(e = 9\)、面の数 \(f = 5\) より、
\(\begin{align}v − e + f &= 6 − 9 + 5 \\&= 2\end{align}\)
(例3)四角錐
頂点の数 \(v = 5\)、辺の数 \(e = 8\)、面の数 \(f = 5\) より、
\(\begin{align}v − e + f &= 5 − 8 + 5 \\&= 2\end{align}\)
確かにオイラーの多面体定理 \(v − e + f = 2\) が成り立ちますね!
オイラーの多面体定理の覚え方
オイラーの多面体定理は、「\(v\), \(e\), \(f\) って、何が何だっけ…。」「どれを引くんだっけ…。」と結構忘れやすい定理ですよね。
オイラーの多面体定理には、有名な語呂合わせがあります。
線は帳面に引け
\begin{align}\color{skyblue}{\text{(辺 $e$)} =} \color{orange}{ \text{(頂点 $v$)}} + \color{limegreen}{\text{(面 $f$)}} \color{red}{− 2}\end{align}
移項するとちゃんと \(v − e + f = 2\) になります。
記号じゃ覚えにくい!という人は、この語呂合わせを覚えておくとよいでしょう。
どうしてもオイラーの多面体定理の公式を思い出せない場合は、簡単な多面体を書いて頂点、辺、面の数を数えましょう。
「\(2\) つ足して \(1\) つ引くと数が \(2\) になる」ことさえ押さえておけば、簡単に確認できます。
オイラーの多面体定理の証明
ここでは、オイラーの多面体定理が成り立つことを証明していきます。
立体のまま考えるのは少し大変なので、多面体を平面グラフに変換して考えます。
【補足①】平面グラフとは?
平面グラフとは、平面上の頂点集合とそれを交差なく結ぶ辺集合からなるグラフのことです。
次の特徴を満たしている必要があります。
- 頂点は必ず辺で別の頂点に結ばれる
- 辺同士は交差しない
(辺は曲線でもOK)
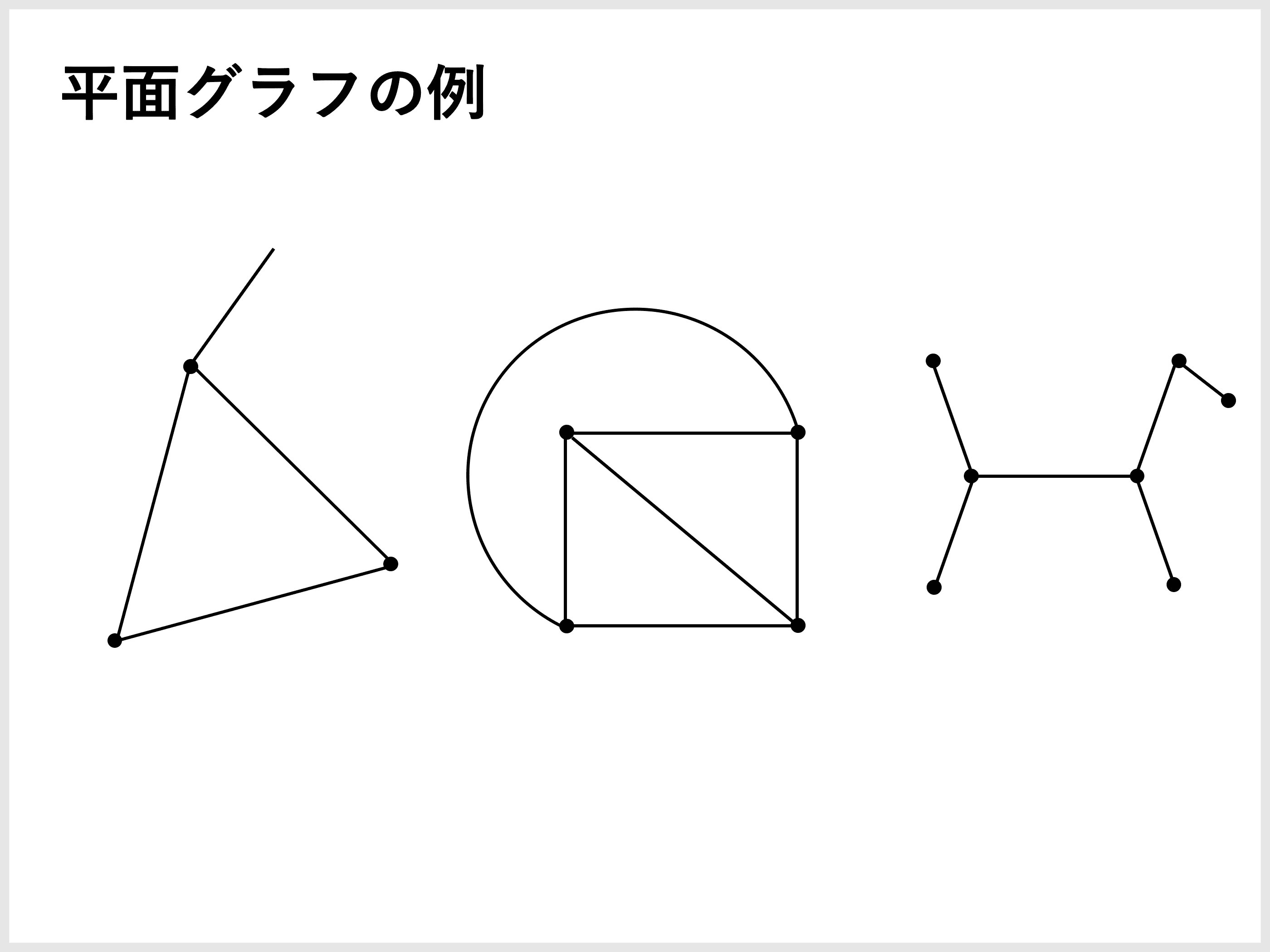
また、平面グラフにおける面は、辺で囲まれた閉領域と、外側に広がる開領域です。

【補足②】多面体 ⇄ 平面グラフの変換
多面体の \(1\) つの面に穴を開けて無理やり広げると、平面グラフに変換できるという面白い性質があります。

このとき、なんと頂点・辺・面の数は変わりません。
したがって、平面グラフで \(v − e + f = 2\) が成り立つことが証明できれば、多面体でも成り立つといえますね。
【証明】オイラーの多面体定理を示す
この証明は、数学的帰納法で進めることができます。
少し難しい証明なので、流れがざっくりと理解できればOKです!
頂点の数 \(v\)、辺の数 \(e\)、面の数 \(f\) の平面グラフを考える。
すべての自然数 \(v\), \(e\), \(f\) について \(v − e + f = 2\) …① が成り立つことを数学的帰納法によって示す。
(i) \(e = 1\) のとき

\(v = 2\)、\(e = 1\)、\(f = 1\) より、
\(v − e + f = 2 − 1 + 1 = 2\)
となるので、①は成り立つ。
(ii) \(e = k\) のとき、①が成り立つと仮定する。
このときの \(v\), \(e\), \(f\) をそれぞれ \(v_k\), \(e_k\), \(f_k\) とおくと、
\(v_k − e_k + f_k = 2\) …②

このとき、辺を \(1\) 本追加することを考える (\(e_{k + 1} = e_k + 1\))。
辺は点同士をつなぐため、次の \(2\) 通りの追加のしかたがある。
(a) 新しい頂点と既存の頂点を結ぶ辺を追加する場合

辺の数 \(e_{k + 1}\) は \(e_k + 1\)
頂点の数も \(1\) つ増えるので \(v_{k + 1} = v_k + 1\)
面の数は変わらないので \(f_{k + 1} = f_k\)
よって、
\(v_{k + 1} − e_{k + 1} + f_{k + 1}\)
\(= (v_k + 1) − (e_k + 1) + f_k\)
\(= v_k − e_k + f_k\)
\(= 2\)
となり、①は成り立つ。
(b) 既存の頂点同士を結ぶ辺を追加する場合
(\(2\) 頂点、または同一の頂点)

辺の数 \(e_{k + 1}\) は \(e_k + 1\)
頂点の数は変わらないので \(v_{k + 1} = v_k\)
面の数は \(1\) つ増えるので \(f_{k + 1} = f_k + 1\)
よって、
\(v_{k + 1} − e_{k + 1} + f_{k + 1}\)
\(= v_k − (e_k + 1) + (f_k + 1)\)
\(= v_k − e_k + f_k\)
\(= 2\)
となり、①は成り立つ。
(a), (b) より、\(e = k + 1\) のときも①は成り立つ。
以上から、任意の平面グラフで \(v − e + f = 2\) が成り立つことが示された。
したがって、頂点の数 \(v\)、辺の数 \(e\)、面の数 \(f\) である任意の凸多面体において、オイラーの多面体定理 \(v − e + f = 2\) は成り立つ。
(証明終わり)
オイラーの多面体定理の練習問題
以下の練習問題を通して、オイラーの多面体定理の使い方を説明します。
練習問題①「八面体の辺の数を求める」
面の数と頂点の数が等しい \(n\) 面体を考える。
\(n = 8\) のときの辺の数を答えよ。

面の数と頂点の数がわかっています。
オイラーの多面体定理を使えば簡単ですね!
辺の数を \(e\) とおくと、オイラーの多面体定理より、
\(8 − e + 8 = 2\)
\(e = 14\)
答え: \(\color{red}{14}\) 本
練習問題②「正十二面体の辺の数を求める」
正十二面体の辺の数を求めなさい。
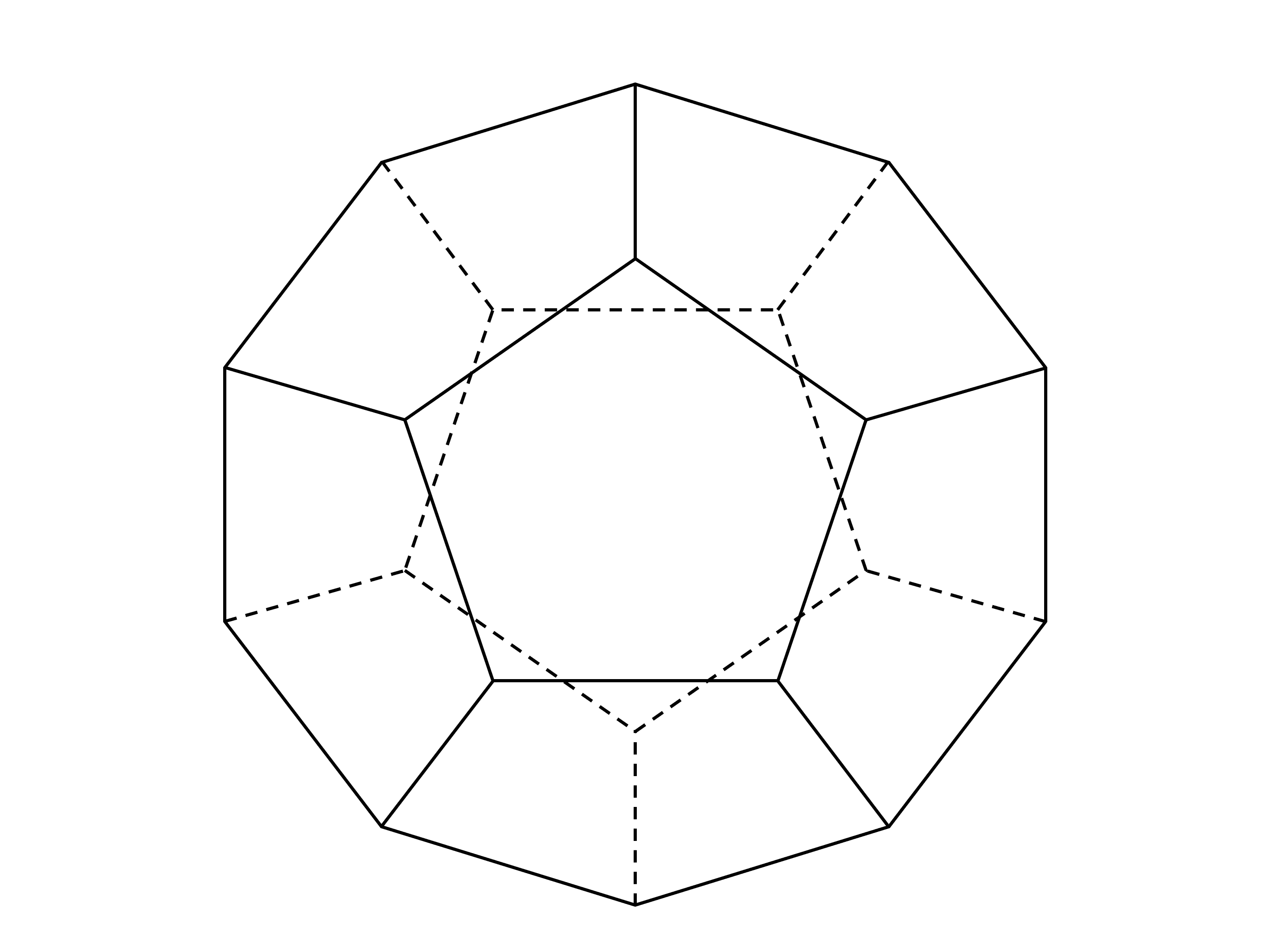

図を書いて数え上げるのは大変ですね。
オイラーの多面体定理を利用しましょう!
頂点の数を \(v\)、辺の数を \(e\)、面の数を \(f\) とおく。
正十二面体の面の数は \(12\) なので、
\(f = 12\)
また、面は正五角形なので \(1\) つの面につき頂点は \(5\) つある。
よって、\(12 \times 5 = 60\)
このうち、\(1\) つの頂点につき \(3\) つの面が接しているため、\(3\) で割ると
\(60 \div 3 = 20\)
よって、\(v = 20\)
ここで、オイラーの多面体定理より
\(v − e + f = 2\)
\(20 − e + 12 = 2\)
\(e = 30\)
答え: \(\color{red}{30}\) 本
練習問題③「サッカーボールの面の数を求める」
サッカーボールは、正五角形と正六角形のパネルを合わせて計 \(32\) 枚のパネルでできている。
このとき、正五角形と正六角形それぞれのパネルの枚数を求めよ。

パネルとは面のことですね。
それぞれのパネルの枚数を \(x\), \(y\) とおいて、オイラーの多面体定理を利用しましょう。
正五角形のパネルの枚数を \(x\) 枚、正六角形のパネルの枚数を \(y\) 枚とおく。
サッカーボールの面の数は
\((x + y)\) 枚 …①
正五角形 \(x\) 枚の辺の数は \(5x\)、正六角形 \(y\) 枚の辺の数は \(6y\)。
そして、\(1\) つの辺に \(2\) つのパネルの辺が重なりあうので、サッカーボールの辺の数は
\(\displaystyle \frac{1}{2} (5x + 6y)\) 本 …②
また、正五角形 \(x\) 枚の頂点の数は \(5x\)、正六角形 \(y\) 枚の頂点の数は \(6y\)。
\(1\) つの頂点に \(3\) つのパネルの頂点が重なりあうので、サッカーボールの頂点の数は
\(\displaystyle \frac{1}{3} (5x + 6y)\) 個 …③
①、②、③をオイラーの多面体定理に当てはめて、
\(\displaystyle \frac{1}{3} (5x + 6y) − \frac{1}{2} (5x + 6y) + (x + y) = 2\)
両辺に \(6\) をかけて
\(2(5x + 6y) − 3(5x + 6y) + 6(x + y) = 12\)
\(10x + 12y − 15x − 18y + 6x + 6y = 12\)
\(x = 12\)
ここで、サッカーボールのパネルの総数は \(32\) 枚なので、
\(\begin{align} y &= 32 − x \\ &= 32 − 12 \\ &= 20 \end{align}\)
答え: 正五角形 \(\color{red}{12}\) 枚、正六角形 \(\color{red}{20}\) 枚
以上で練習問題も終わりです!
高校数学ではさらっと習うだけの定理ですが、数学の一分野「トポロジー(位相幾何学)」の始まりとなった重要な定理です。
この記事を通してオイラーの多面体定理についての理解が深まれば幸いです!

