この記事では、「平均値の定理」についてわかりやすく解説します。
不等式の証明や、漸化式の極限における平均値の定理の使い方を例題を通してていねいに説明していきますので、ぜひマスターしてくださいね！
目次
平均値の定理とは？
平均値の定理は、曲線の傾きの平均と、曲線上の \(1\) 点における傾きに関して成り立つ定理です。
開区間 \((a, b)\) で微分可能かつ \(x = a, b\) で連続な関数 \(f(x)\) に対し、
\begin{align}\color{red}{\displaystyle \frac{f(b) − f(a)}{b − a} = f’(c)}\end{align}
\begin{align}\color{red}{a < c < b}\end{align}
を満たす実数 \(c\) が存在する。
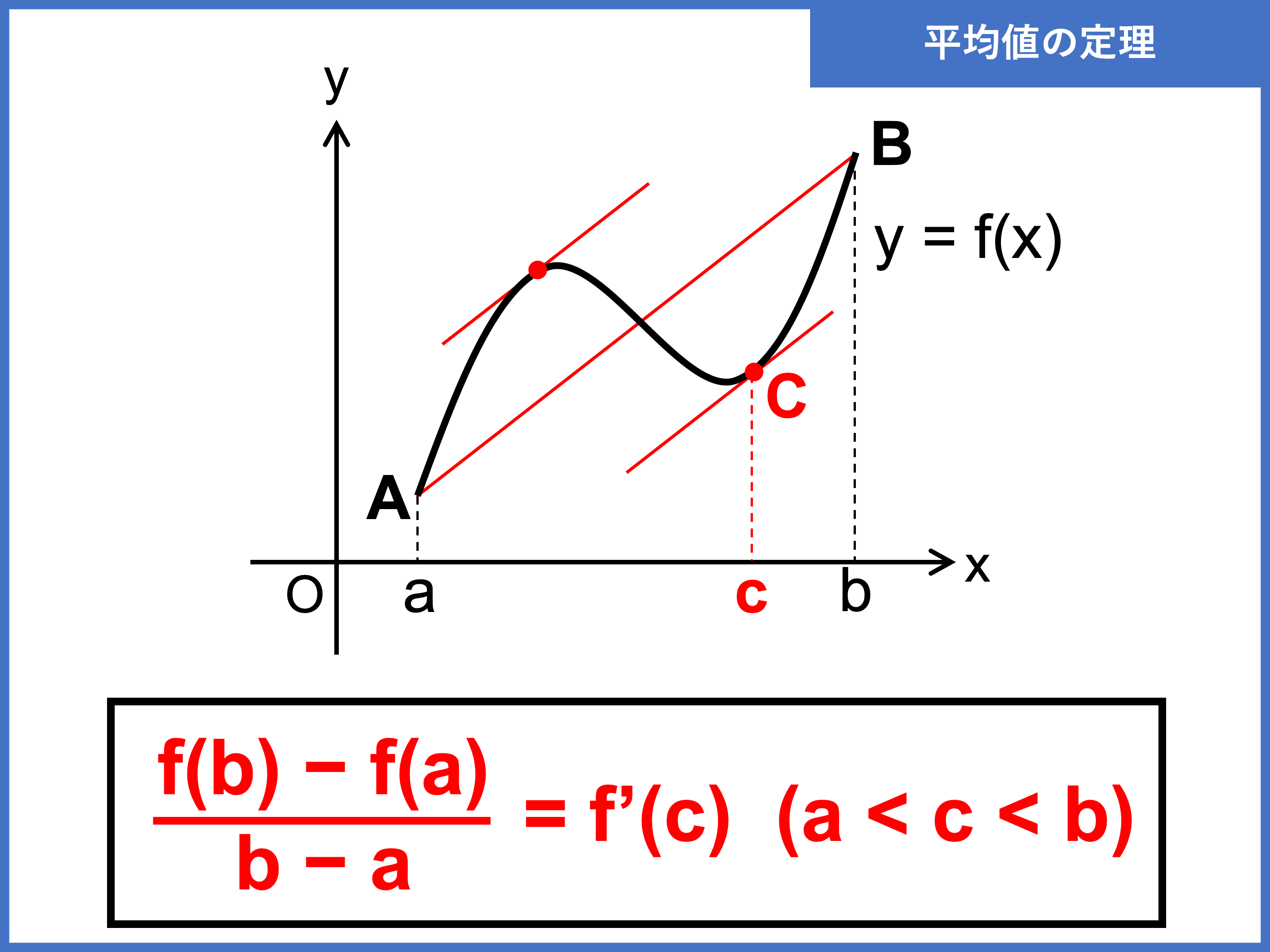
この定理は、曲線上のある点における傾きが区間の両端を結んだ平均の傾きと必ずどこかで等しくなる（平行になる）ことを示しています。
平均値の定理が成り立つ理由
平均値の定理が成り立つ理由を、背理法で考えてみましょう。
定理が成り立たないと仮定します。
微分係数 \(f’(x)\) は \((a, b)\) において連続に変化しますから、定理が成り立たないことは曲線の傾きが直線の傾きより常に大きいまたは小さいことを意味します。
そうするといつまでたっても \((a, f(a))\) を出発した点が \((b, f(b))\) にたどり着けません。
よって、仮定が矛盾していることから、平均値の定理が成り立つとわかります。
ここでは割愛しますが、平均値の定理を厳密に示すには、次の \(2\) つの定理を先に証明する必要があります。
- 最大値・最小値の定理
閉区間で連続な関数は、その閉区間で最大値および最小値をもつ。 - ロルの定理
関数 \(f(x)\) が閉区間 \([a,b]\) で連続、開区間 \((a,b)\) で微分可能で、\(f(a) = f(b)\) ならば、
\begin{align}f’(c) = 0, \ a < c < b\end{align}
を満たす実数 \(c\) が存在する。
また、平均値の定理はロルの定理の適用条件を広げてあげたものと捉えるとわかりやすいですね。
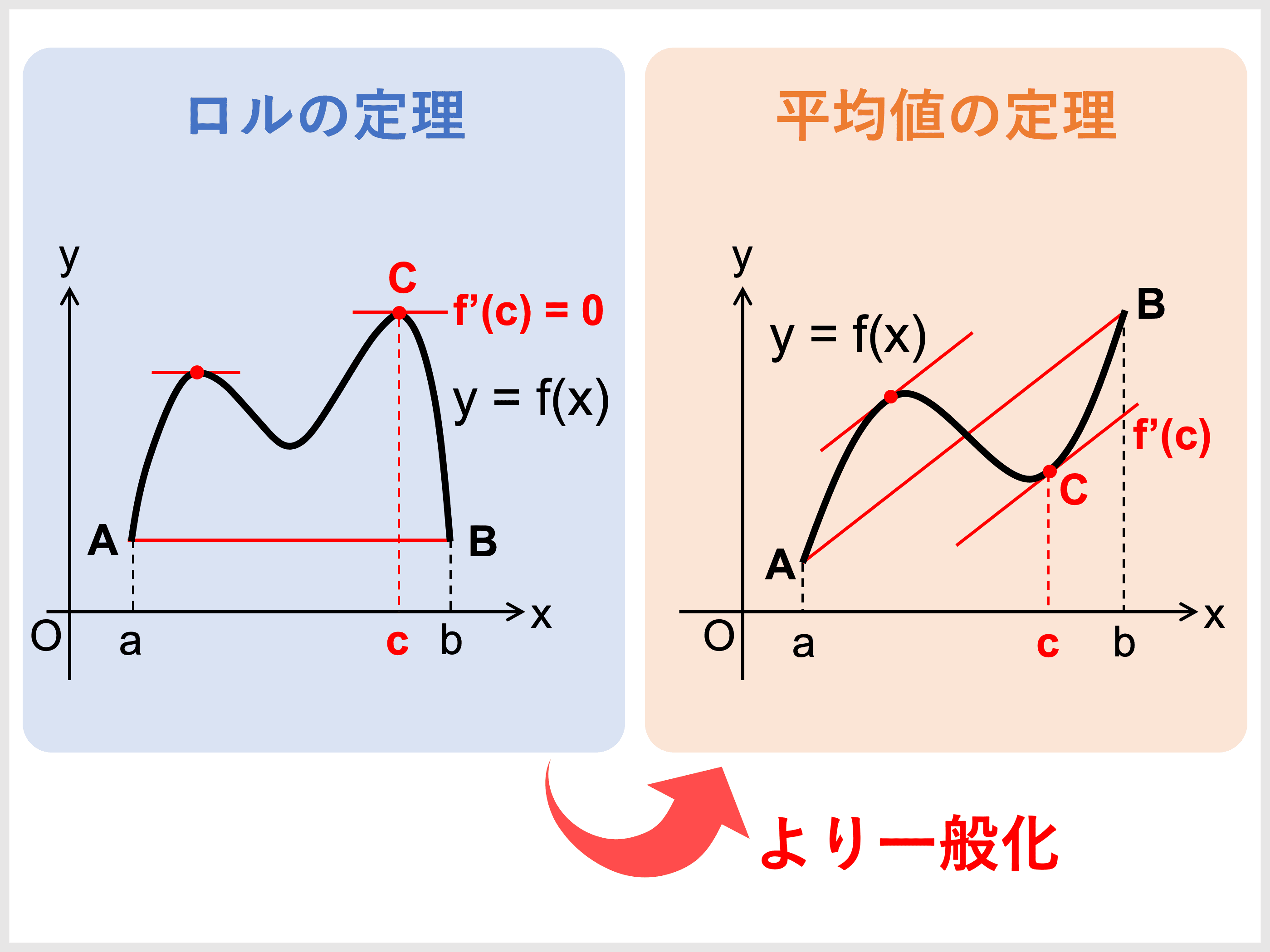
平均値の定理の使いどころ
平均値の定理を使うのは、主に「不等式の証明」と「漸化式の極限」の問題です。
定理自体はシンプルな平均値の定理ですが、具体的にどのような問題で使えるのかを見抜くには訓練が必要です。
典型的なパターンを学んで、「平均値の定理を使えば解ける」問題に気づけるようになりましょう。
平均値の定理の使い方① 不等式の証明
平均値の定理を使う問題としてよくあるのが不等式の証明です。
特に、証明する不等式の中に \(f(b) − f(a)\) や \(b − a\) の形が登場するときは、平均値の定理を疑います。
例題「\(\log b − \log a < b − a\) を示す」
次の例題で、不等式の証明における平均値の定理の使い方を説明します。
\(b > a > 1\) のとき、
\(\log b − \log a < b − a\)
を示せ。
証明する不等式の中に \(f(b) − f(a)\) や \(b − a\) の形があれば、平均値の定理が使えるだろうと判断します。
例題において \(f(x) = \log x\) とみると、\(f(b) − f(a) < b − a\) となっており、平均値の定理が使えそうです。
平均値の定理を使うには、式変形して無理やり傾きの形 \(\displaystyle \frac{f(b) − f(a)}{b − a}\) を作ります。
このときに両辺の割り算が必要な場合は、割る数（除数）が \(0\) でないこと、およびその正負を必ず確認します。
\(\log b − \log a < b − a\)
\(b − a > 0\) より、両辺を \(b − a\) で割ることができて、
\(\displaystyle \frac{\log b − \log a}{b − a} < 1\)
ここで、平均値の定理（\(\displaystyle \frac{f(b) − f(a)}{b − a} = f’(c)\), \(a < c < b\) を満たす実数 \(c\) が存在すること）を宣言します。
\(f'(x)\) を先に求めておくとスムーズです。
また、設問で与えられた定数の範囲の条件（今回は \(b > a > 1\)）は答えに影響するので、定理の宣言にも必ず追加しておきましょう。
\(\displaystyle (\log x)’ = \frac{1}{x}\) であるから、平均値の定理より
\(\displaystyle \frac{\log b − \log a}{b − a} = \frac{1}{c}\)
\(b > c > a > 1\)
を満たす実数 \(c\) が存在する。
最後に、変形しておいた不等式と平均値の定理の式に登場する値の大小関係を比較して、不等式が成り立つことを示します。
今回は、左辺が \(1\) より小さいことを示したいので、\(\displaystyle \frac{1}{c} < 1\) を示せばよいですね。
ここで、\(\displaystyle \frac{1}{x}\) は \(x > 0\) で単調減少するので
\(\displaystyle \frac{1}{c} < \frac{1}{a} < 1\)
したがって、\(\displaystyle \frac{\log b − \log a}{b − a} = \frac{1}{c} < 1\)
すなわち
\(\color{red}{\displaystyle \frac{\log b − \log a}{b − a} < 1}\)
\(b − a > 0\) より、両辺を \(b − a\) で割ることができて、
\(\displaystyle \frac{\log b − \log a}{b − a} < 1\)
\(\displaystyle (\log x)’ = \frac{1}{x}\) であるから、平均値の定理より
\(\displaystyle \frac{\log b − \log a}{b − a} = \frac{1}{c}\)
\(b > c > a > 1\)
を満たす実数 \(c\) が存在する。
ここで、\(\displaystyle \frac{1}{x}\) は \(x > 0\) で単調減少するので
\(\displaystyle \frac{1}{c} < \frac{1}{a} < 1\)
したがって、\(\displaystyle \frac{\log b − \log a}{b − a} = \frac{1}{c} < 1\)
すなわち
\(\color{red}{\displaystyle \frac{\log b − \log a}{b − a} < 1}\)
（証明終わり）
このように、不等式が成り立つことを示せました。
ポイントは、平均値の定理が使えると気づくこと、そして \(a < c < b\) を踏まえて \(f’(c)\) の範囲を評価することです。
平均値の定理の使い方② 漸化式と極限
平均値の定理を次のように応用すると、漸化式の極限の問題でも使える場合があります。
平均値の定理
\begin{align}\displaystyle \frac{f(b) − f(a)}{b − a} = f’(c), a < c < b\end{align}
において \(\color{red}{b = n + 1}\), \(\color{red}{a = n}\) とすると、
\begin{align}\displaystyle \frac{f(n + 1) − f(n)}{(n + 1) − n} = f’(c_n)\end{align}
すなわち
\(\color{red}{f(n + 1) − f(n) = f’(c_n)}\)、\(\color{red}{n < c_n < n + 1}\)
このように、漸化式の形が得られます。
このことを利用すると、「\(\displaystyle \lim_{n \to \infty} (A_{n + 1} − A_n)\) を求めよ」といった問題で、一般項 \(A_n\) が微分可能な関数であれば平均値の定理を使用できます。
例題「\(\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right)\) を求める」
次の例題で、漸化式の極限における平均値の定理の使い方を説明します。
\(\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right)\) を求めよ。
ただし \(\displaystyle \lim_{x \to \infty} \frac{x}{e^x} = 0\) を用いてよい。
漸化式の形に注目し、平均値の定理が使えるかを判断します。
\(\displaystyle f(x) = \frac{x − 1}{e^x}\) と見ると、
\(\begin{align}\displaystyle \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} &= f(n + 1) − f(1) \\&= \displaystyle \frac{f(n + 1) − f(1)}{(n + 1) − n}\end{align}\)
となり、平均値の定理を適用できそうです。
平均値の定理（\(\displaystyle \frac{f(n + 1) − f(n)}{(n + 1) − n} = f’(c)\), \(n < c_n < n + 1\) を満たす \(c_n\) が存在すること）を宣言します。
\(f'(x)\) を先に求めておくとスムーズです。
\(\displaystyle f(x) = \frac{x − 1}{e^x}\) とすると
\(\begin{align} f’(x) &= \{(x − 1)e^{−x}\}’ \\ &= (x − 1)’e^{−x} + (x − 1) (e^{−x})’ \\ &= \frac{2 − x}{e^x} \end{align}\)
平均値の定理より、
\(\displaystyle \frac{\frac{n}{e^{n + 1}} − \frac{n − 1}{e^n}}{(n + 1) − n} = \frac{2 − c_n}{e^{c_n}}\)
\(n < c_n < n + 1\)
を満たす \(c_n\) が存在する。
この \(c_n\) と \(n\) との大小関係を利用して、極限を求められないかを考えます。
追い出しの原理またははさみうちの原理を利用することが多いです。
\(n < c_n\) より、\(\displaystyle \lim_{n \to \infty} c_n = \infty\)
さらに、\(\displaystyle \lim_{x \to \infty} \frac{x}{e^x} = 0\) から
\(\displaystyle \lim_{c_n \to \infty} \frac{2 − c_n}{e^{c_n}} = 0\)
したがって
\(\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right)\)
\(\displaystyle = \lim_{c_n \to \infty} \frac{2 − c_n}{e^{c_n}}\)
\(= 0\)
答え： \(\color{red}{\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right) = 0}\)
\(\displaystyle f(x) = \frac{x − 1}{e^x}\) とすると
\(\begin{align} f’(x) &= \{(x − 1)e^{−x}\}’ \\ &= (x − 1)’e^{−x} + (x − 1) (e^{−x})’ \\ &= \frac{2 − x}{e^x} \end{align}\)
平均値の定理より、
\(\displaystyle \frac{\frac{n}{e^{n + 1}} − \frac{n − 1}{e^n}}{(n + 1) − n} = \frac{2 − c_n}{e^{c_n}}\)
\(n < c_n < n + 1\)
を満たす \(c_n\) が存在する。
\(n < c_n\) より、\(\displaystyle \lim_{n \to \infty} c_n = \infty\)
さらに、\(\displaystyle \lim_{x \to \infty} \frac{x}{e^x} = 0\) から
\(\displaystyle \lim_{c_n \to \infty} \frac{2 − c_n}{e^{c_n}} = 0\)
したがって
\(\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right)\)
\(\displaystyle = \lim_{c_n \to \infty} \frac{2 − c_n}{e^{c_n}}\)
\(= 0\)
答え： \(\color{red}{\displaystyle \lim_{n \to \infty} \left( \frac{n}{e^{n + 1}} − \frac{n − 1}{e^n} \right) = 0}\)
漸化式の極限の問題では、平均値の定理を使うこと自体に気づくのがやや難しいため、いろいろな問題に触れて経験を積むことをオススメします！
平均値の定理の練習問題
それでは、平均値の定理を使った練習問題に挑戦しましょう。
練習問題①「log を含む不等式を示す」
\(e < p < q\) のとき次の不等式を示せ。
\(\displaystyle \log(\log q) − \log(\log p) < \frac{q − p}{e}\)
なんとこれ、名古屋大の入試で出題された問題です。
難関大の問題も、今回学んだことをベースに考えればクリアできます。
「\(f(q) − f(p)\)」「\(q − p\)」に注目し、平均値の定理を使います。
\(f(x) = \log(\log x)\) とすると
\(\begin{align} f’(x) &= \frac{1}{\log x} \cdot (\log x)’ \\ &= \frac{1}{x \log x} \end{align}\)
また、\(q − p > 0\) より
\(\displaystyle \log(\log q) − \log(\log p) < \frac{q − p}{e}\)
\(\displaystyle \iff \frac{\log(\log q) − \log(\log p)}{q − p} < \frac{1}{e}\)
ここで、平均値の定理より
\(\displaystyle \frac{\log(\log q) − \log(\log p)}{q − p} = \frac{1}{c\log c}\)
\(p < c < q\)
を満たす実数 \(c\) が存在する。
\(e < p < c\) と \(\log x\) の単調増加性より
\(\displaystyle \frac{1}{c} < \frac{1}{e}\)
\(\displaystyle \frac{1}{\log c} < \frac{1}{\log e} = 1\)
すなわち
\(\displaystyle \frac{1}{c\log c} < \frac{1}{e}\)
よって
\(\displaystyle \frac{\log(\log q) − \log(\log p)}{q − p} = \frac{1}{c\log c} < \frac{1}{e}\)
したがって、
\(\displaystyle \log(\log q) − \log(\log p) < \frac{q − p}{e}\)
は成り立つ。
（証明終わり）
練習問題②「漸化式の極限を求める」
\(\displaystyle a_n = \frac{(\log n)^2}{2}\) とする。
\(\displaystyle \lim_{n \to \infty} (a_{n + 1} − a_n)\) を求めよ。
ただし \(\displaystyle \lim_{x \to \infty} \frac{\log x}{x} = 0\) を用いてよい。
前問に続き、これも名古屋大の問題です。
平均値の定理が使えることにさえ気づけば、難関大の問題も解けてしまいますね。
\(\displaystyle f(x) = \frac{(\log x)^2}{2}\) とすると
\(\begin{align} f’(x) &= \frac{2 \log x \cdot (\log x)’}{2} \\ &= \frac{\log x}{x} \end{align}\)
ここで、平均値の定理より
\(a_{n + 1} − a_n\)
\(\displaystyle = \frac{\frac{(\log (n + 1))^2}{2} + \frac{(\log n)^2}{2}}{(n + 1) − n}\)
\(= f’(c_n)\)
\(\displaystyle = \frac{\log c_n}{c_n}\)
\(n < c_n < n + 1\)
を満たす \(c_n\) が存在する。
\(\displaystyle \lim_{x \to \infty} \frac{\log x}{x} = 0\) より、
\(\displaystyle \lim_{n \to \infty} \frac{\log c_n}{c_n} = 0\)
よって
\(\displaystyle \lim_{n \to \infty} (a_{n + 1} − a_n) = \lim_{n \to \infty} \frac{\log c_n}{c_n} = 0\)
答え： \(\color{red}{0}\)
以上で解説は終わりです。
平均値の定理は、使える問題に気づくことがポイントです。
いざというときに平均値の定理を使うことを見抜けるよう、練習を重ねておきましょう。
「極限」に関するほかの公式や定理については、以下のまとめ記事から探してみてください！
極限・微分積分を総まとめ！高校で習う定理・公式一覧