この記事では、和の記号「シグマ \(\sum\)」の意味や公式をわかりやすく解説していきます。
公式の証明や計算問題の解き方も説明していきますので、ぜひこの記事を通してマスターしてくださいね。
目次
シグマ \(\sum\) とは?
シグマ \(\sum\) とは、与えられた条件を満たす数の総和を表す省略記号です。
シグマ \(\sum\) を使うときは、次の \(3\) つを指定します。
① 変数、② はじめと終わりの値、③ 条件式

シグマ \(\sum\) の計算では、条件式の変数 \(k\) に代入する値を \(1\) ずつ増やし、それらを足していきます。
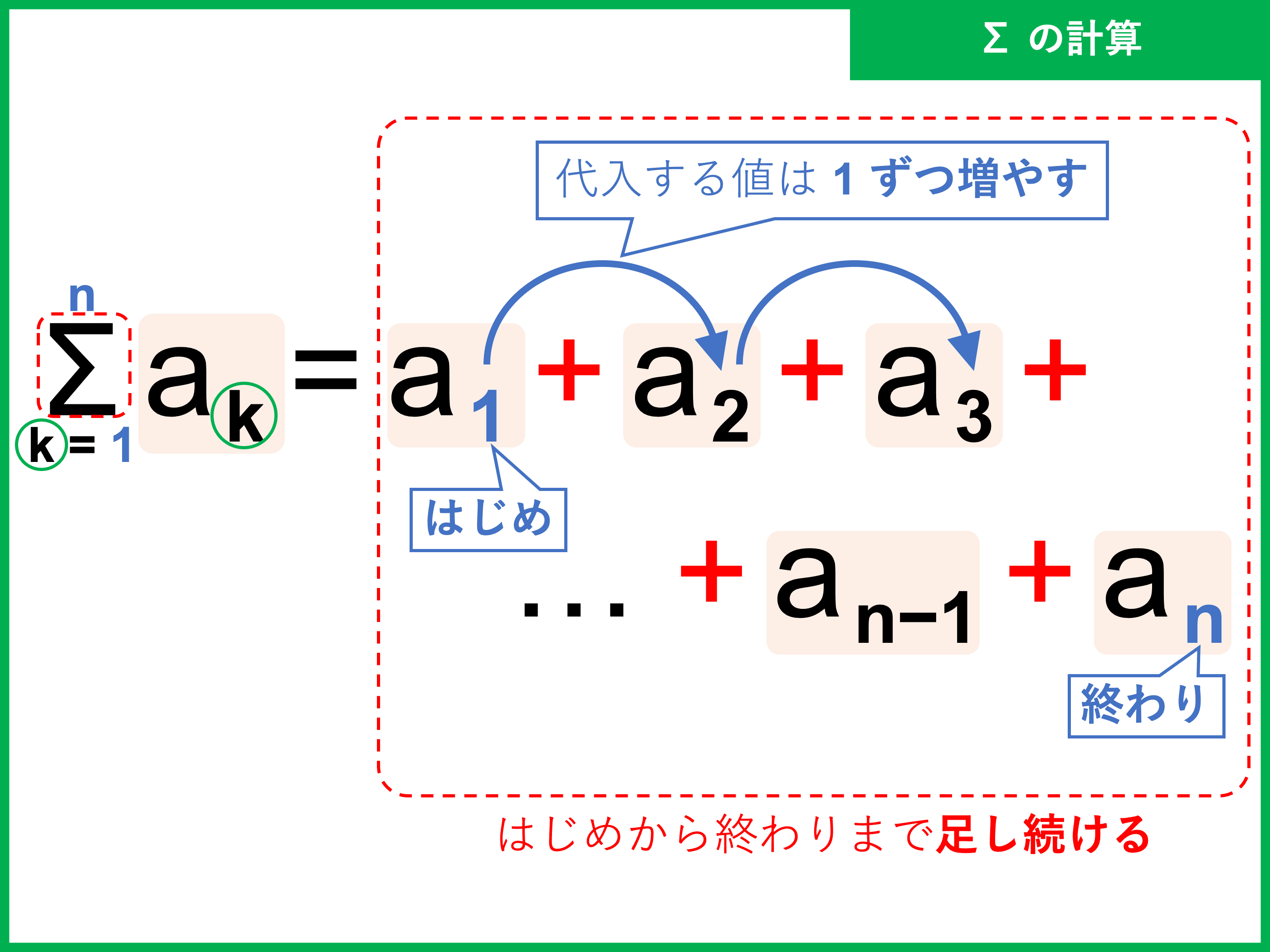
つまり、「使う変数」「変数に代入するはじめと終わりの値」「具体的な条件式」がそろえば計算できます。
シグマ \(\sum\) は、規則的な数の足し算を表すのにとても便利です。
例えば、\(1\) から \(100\) までの自然数の足し算は、
\(1 + 2 + 3 + 4 + \cdots + 100\) \(= \color{salmon}{\displaystyle \sum_{k=1}^{100} k}\)
と表せます。
シグマ \(\sum\) を使うと、足し算を「\(◯ + ◯ + \cdots\)」と律儀に書くよりも、とてもスッキリと表現できますね。
「\(\sum\)」は、規則的に変化する数字を足し続ける計算。
そのため、数列の和を表すときなどによく使われます。
シグマ \(\sum\) の性質と証明
シグマ \(\sum\) の計算を行う上で、必ず利用する重要な性質があります。
\(p\), \(q\) は \(k\) に無関係な定数とする。
- \(\displaystyle \sum_{k=1}^n pa_k = p\sum_{k=1}^n a_k\)
- \(\displaystyle \sum_{k=1}^n (a_k \pm b_k) = \sum_{k=1}^na_k \pm \sum_{k=1}^nb_k\)
- \(\displaystyle \sum_{k=1}^n (pa_k \pm qb_k) = p\sum_{k=1}^n a_k \pm q\sum_{k=1}^n b_k\)
- \(\displaystyle \sum_{k=1}^n a_k = \sum_{i=1}^n a_i\)
それぞれの性質とその証明を詳しく見ていきましょう。
【性質①】係数は外に出せる
条件式に係数がかかっている場合、\(\sum\) の外に出せます。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n pa_k = p\sum_{k=1}^n a_k}\end{align}
(\(p\) は \(k\) に無関係な定数)
足していくすべての項に同じ係数がかかっているので、当然くくり出すことができますね。
\(\displaystyle \sum_{k=1}^n pa_k\)
\(= pa_1 + pa_2 + pa_3 + \cdots + pa_n\)
\(= p(a_1 + a_2 + a_3 + \cdots + a_n)\)
\(\displaystyle = p\sum_{k=1}^n a_k\)
(証明終わり)
【性質②】多項式では ∑ を分配できる
条件式が多項式の場合、多項式のまま \(\sum\) の計算をしても、最初から項ごとに \(\sum\) の計算をしても結果は同じです。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n (a_k \pm b_k) = \sum_{k=1}^n a_k \pm \sum_{k=1}^n b_k}\end{align}
性質①と合わせて、
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n (pa_k \pm qb_k) = p\sum_{k=1}^n a_k \pm q\sum_{k=1}^n b_k}\end{align}
(\(p\), \(q\) は \(k\) に無関係な定数)
\(\sum\) の式を展開して並べ替えてみると、この性質が成り立つことがすぐにわかります。
\(\displaystyle \sum_{k=1}^n (a_k \pm b_k)\)
\(= (a_1 \pm b_1) + (a_2 \pm b_2) + \cdots + (a_n \pm b_n)\)
\(= (a_1 + a_2 + \cdots + a_n)\) \( \pm \ (b_1 + b_2 + \cdots + b_n)\)
\(\displaystyle = \sum_{k=1}^n a_k \pm \sum_{k=1}^n b_k\)
\(\displaystyle \sum_{k=1}^n (pa_k \pm qb_k)\)
\(= (pa_1 \pm qb_1) + (pa_2 \pm qb_2) \,+ \) \(\cdots + (pa_n \pm qb_n)\)
\(= (pa_1 + pa_2 + \cdots + pa_n) \) \(\pm \,(qb_1 + qb_2 + \cdots + qb_n)\)
\(= p(a_1 + a_2 + \cdots + a_n) \) \(\pm \,q(b_1 + b_2 + \cdots + b_n)\)
\(\displaystyle = p\sum_{k=1}^n a_k \pm q\sum_{k=1}^n b_k\)
(証明終わり)
繰り返し計算である \(\sum\) の中身はシンプルな方がよいので、
- 係数がかかっていたら前に出す
- 多項式の \(\bf{\sum}\) は単項式の \(\bf{\sum}\) に分ける
を徹底しましょう!
(例)
- \(\displaystyle \sum_{k=1}^n (3k^2 + 2) = 3\sum_{k=1}^n k^2 + \sum_{k=1}^n 2\)
- \(\displaystyle \sum_{k=1}^n (8k^3 − 2k + 1) \) \(\displaystyle = 8\sum_{k=1}^n k^3 − 2\sum_{k=1}^n k + \sum_{k=1}^n 1\)
- \(\displaystyle \sum_{k=1}^n (5^k + 3 \cdot 2^k) = \sum_{k=1}^n 5^k + 3\sum_{k=1}^n 2^k\)
【性質③】変数はなんでもいい
条件式の形が同じならば、変数が置き換わっても計算結果はまったく同じです。
\begin{align}\displaystyle \sum_{\color{red}{k}=1}^n a_\color{red}{k} = \sum_{\color{red}{i}=1}^n a_\color{red}{i}\end{align}
変数は慣習的に「\(k\)」が使われることが多いですが、別の文字が使われることも当然あります。
文字の違いに惑わされないようにしましょう!
シグマ \(\sum\) の公式と証明
シグマ \(\sum\) は規則的な数の足し算なので、足し算の結果にも規則性があります。
ここでは、代表的な和の公式を確認しましょう。
\(c\), \(r\) は \(k\) に無関係な定数とする。
- \(\displaystyle \sum_{k=1}^n c = nc\)
特に \(\displaystyle \sum_{k=1}^n1 = n\) - \(\displaystyle \sum_{k=1}^n k = \frac{1}{2} n(n + 1)\)
- \(\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6} n(n + 1)(2n + 1)\)
- \(\displaystyle \sum_{k=1}^n k^3 = \left\{ \frac{1}{2} n(n + 1) \right\}^2\)
- \(\displaystyle \sum_{k=1}^n r^{k−1} = \frac{1 − r^n}{1 − r} = \frac{r^n − 1}{r − 1}\) \((r \neq 1)\)
それぞれの公式とその証明を詳しく見ていきましょう。
【公式①】定数項の和
定数項(変数を含まない項)の和を求めるときは、足す回数(= 項数)がポイントです。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n c = nc}\end{align}
特に \(\color{red}{\displaystyle \sum_{k=1}^n 1 = n}\)
(\(c\) は \(k\) に無関係な定数)
\(\sum\) の計算の意味を考えると、定数項 \(c\) を \(n\) 回足すことになりますね。
\(\displaystyle \sum_{k=1}^n c\)
\(= c + c + c + \cdots + c\)
(\(1 \sim n\) までの \(n\) 回)
\(= nc\)
(証明終わり)
公式①の計算上の注意点
この公式を、「単純に \(n\) をかければいい!」と覚えるのは危険です。
重要なのは「定数項を足す回数 = 項数」なので、代入するはじめの値と終わりの値から、項数を必ず確認しましょう。
\(A\), \(B\) を自然数 \((A < B)\) とすると、\(\displaystyle \sum_{k= A}^B a_k\) の項数は
\begin{align}\color{red}{B − A + 1}\end{align}
(例)
- \(\displaystyle \sum_{k=1}^n 1\)
項数は \(n − 1 + 1 = n\) なので、
\(\displaystyle \sum_{k=1}^n 1 = n \cdot 1 = \color{red}{n}\) - \(\displaystyle \sum_{k=3}^6 c\)
項数は \(6 − 3 + 1 = 4\) なので、
\(\displaystyle \sum_{k=3}^6 c = \color{red}{4c}\) - \(\displaystyle \sum_{k=2}^{n−1} 7\)
項数は \((n − 1) − 2 + 1 = n − 2\) なので、
\(\displaystyle \sum_{k=2}^{n−1} 7 = \color{red}{7(n − 2)}\)
項数を把握することは、以降の公式を使うときも重要です。
特に \(k = 1 \sim n\) 以外のときは、よ〜く注意しておきましょう!
【公式②】自然数の和
使用頻度の高い公式なので、必ず覚えましょう。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n k = \frac{1}{2} n(n + 1)}\end{align}
展開してみると、実は等差数列の和を求めていることがわかります。
 等差数列をわかりやすく解説!一般項や和の公式の覚え方
等差数列をわかりやすく解説!一般項や和の公式の覚え方
\(\displaystyle \sum_{k=1}^n k \) \(= 1 + 2 + 3 + \cdots + n\)
これは初項 \(1\)、末項 \(n\)、項数 \(n\) の等差数列の和であるから、
\(\displaystyle \sum_{k=1}^n k = \frac{1}{2} n(n + 1)\)
(証明終わり)
公式②の計算上の注意点
\(k = 1 \sim n\) のときは何も考えずに公式通りでOKです。
(例)
\(\begin{align}\displaystyle \sum_{k=1}^n 3k &= 3\sum_{k=1}^n k\\&= 3 \cdot \frac{1}{2} n(n + 1)\\&= \color{red}{\frac{3}{2} n(n + 1)}\end{align}\)
終わりの値が \(\bf{n}\) 以外のときは、公式 \(\displaystyle \frac{1}{2} \color{salmon}{n}(\color{salmon}{n} + 1)\) の \(n\) の部分に実際の値を代入すると考えましょう。
(例)
\(\begin{align}\displaystyle \sum_{k=1}^\color{salmon}{7} k &= \frac{1}{2} \cdot \color{salmon}{7}(\color{salmon}{7} + 1)\\&\displaystyle = \frac{1}{2} \cdot 7 \cdot 8\\&= \color{red}{28}\end{align}\)
\(\begin{align}\displaystyle \sum_{k=1}^{\color{salmon}{n−1}} k &= \frac{1}{2} (\color{salmon}{n − 1}) \{(\color{salmon}{n − 1}) + 1\}\\& \displaystyle = \color{red}{\frac{1}{2} (n − 1)n}\end{align}\)
一方、初項が \(\bf{k \neq 1}\) のときは要注意です。
スタートがずれていると考えづらいので、\(\displaystyle \sum_{k=A}^B k\) のときは次のように考えます。
\begin{align}\displaystyle \sum_{k=A}^B k &= (\text{$A \sim B$ の和)} \\&= \text{($1 \sim B$ の和)} − \text{($1 \sim (A−1)$ の和)}\\&= \sum_{k=1}^B k − \sum_{k=1}^{A − 1} k\end{align}
(見切れる場合は横へスクロール)
(例)
\(\begin{align}\displaystyle \sum_{k=3}^n k &= \sum_{k=\color{salmon}{1}}^\color{salmon}{n} k − \sum_{k=\color{salmon}{1}}^\color{salmon}{2} k\\&= \frac{1}{2} n(n + 1) − (1 + 2)\\&= \frac{1}{2} n(n + 1) − 3\\&= \frac{1}{2} (n^2 + n − 6)\\&= \color{red}{\frac{1}{2} (n − 2)(n + 3)}\end{align}\)
\(\begin{align}\displaystyle \sum_{k=10}^{n−1} k &= \sum_{k=\color{salmon}{1}}^{\color{salmon}{n−1}} k − \sum_{k=\color{salmon}{1}}^\color{salmon}{9} k\\&= \frac{1}{2} (n − 1)n − \frac{1}{2} \cdot 9(9 + 1)\\&= \frac{1}{2} (n − 1)n − \frac{1}{2} \cdot 9 \cdot 10\\&= \frac{1}{2} (n^2 − n − 90)\\&= \color{red}{\frac{1}{2} (n − 10)(n + 9)}\end{align}\)
もちろん、公式を「初項 \(1\)、末項 \(n\)、項数 \(n\) の等差数列の和」と意識できていればそのように計算しても構いません。
\(\displaystyle \sum_{k=1}^n k = \frac{1}{2} n(n + 1)\) より
\begin{align}\displaystyle \sum_{k=A}^B k &= \frac{1}{2} \cdot \text{(項数)} \cdot \text{(初項 $+$ 末項)} \\&= \color{red}{\frac{1}{2} (B − A + 1)(A + B)}\end{align}
ただし、公式では \(n\) が末項でもあり項数でもあるので、焦っているとミスしやすいポイントです。
【公式③】平方数の和
見た目が少し複雑ですが、こちらも頑張って丸暗記しましょう!
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6} n(n + 1)(2n + 1)}\end{align}
証明は少し面倒なので、さらっと流し読みすればOKです。
\((k + 1)^3 = k^3 + 3k^2 + 3k + 1\) より、
\((k + 1)^3 − k^3 = 3k^2 + 3k + 1\) …①
①の恒等式の左辺および右辺の、\(k = 1, 2, \cdots, n\) の和を考えると、
(左辺の和)
\(\displaystyle = \sum_{k=1}^n \{(k + 1)^3 − k^3\}\)
\(\displaystyle = \sum_{k=1}^n (k + 1)^3 − \sum_{k=1}^n k^3\)
\(= \{2^3 + 3^3 + \cdots + (n + 1)^3\} \) \(−\, (1^3 + 2^3 + \cdots + n^3)\)
\(= (n + 1)^3 − 1^3\)
\(= (n + 1)^3 − 1\)
(右辺の和)
\(\displaystyle = \sum_{k=1}^n (3k^2 + 3k + 1)\)
\(\displaystyle = 3\sum_{k=1}^n k^2 + 3\sum_{k=1}^n k + \sum_{k=1}^n 1\)
\(\displaystyle = 3\sum_{k=1}^n k^2 + \frac{3}{2} n(n + 1) + n\)
(左辺の和) = (右辺の和) より、
\(\displaystyle (n + 1)^3 − 1 = 3\sum_{k=1}^n k^2 + \frac{3}{2} n(n + 1) + n\)
よって
\(\displaystyle \sum_{k=1}^n k^2\)
\(\displaystyle = \frac{1}{3} \left\{ (n + 1)^3 − 1 − \frac{3}{2} n(n + 1) − n \right\}\)
\(\displaystyle = \frac{1}{3} \left\{ (n + 1)^3 − \frac{3}{2} n(n + 1) − (n + 1) \right\}\)
\(\displaystyle = \frac{1}{6} (n + 1)\{2(n + 1)^2 − 3n − 2\}\)
\(\displaystyle = \frac{1}{6} (n + 1)\{(2n^2 + 4n + 2) − 3n − 2\}\)
\(\displaystyle = \frac{1}{6} (n + 1)(2n^2 + n)\)
\(\displaystyle = \frac{1}{6} n(n + 1)(2n + 1)\)
(証明終わり)
公式③の計算上の注意点
計算上の注意点は、公式② \(\displaystyle \sum_{k=1}^n k\) と同じです。
(例)
\(\begin{align}\displaystyle \sum_{k=1}^n 3k^2 &= 3\sum_{k=1}^n k^2\\&= 3 \cdot \frac{1}{6} n(n + 1)(2n + 1)\\&= \color{red}{\frac{1}{2} n(n + 1)(2n + 1)}\end{align}\)
\(\displaystyle \sum_{k=1}^{n−1} k^2\)
\(\displaystyle = \frac{1}{6} (n − 1)\{(n − 1) + 1\}\{2(n − 1) + 1\}\)
\(\displaystyle = \color{red}{\frac{1}{6} (n − 1)n(2n − 1)}\)
\(\displaystyle \sum_{k=5}^{20} k^2\)
\(\displaystyle = \sum_{k=\color{salmon}{1}}^{\color{salmon}{20}} k^2 − \sum_{k=\color{salmon}{1}}^\color{salmon}{4} k^2\)
\(\displaystyle = \frac{1}{6} \cdot 20(20 + 1)(2 \cdot 20 + 1) \) \(\displaystyle − \, \frac{1}{6} \cdot 4(4 + 1)(2 \cdot 4 + 1)\)
\(\displaystyle = \frac{1}{6} (20 \cdot 21\cdot 41 − 4 \cdot 5 \cdot 9)\)
\(\displaystyle = \frac{20}{6} (21 \cdot 41 − 9)\)
\(\displaystyle = \frac{10}{3} (861 − 9)\)
\(\displaystyle = \frac{10}{3} \cdot 852\)
\(\displaystyle = \color{red}{2840}\)
【公式④】立方数の和
\(\displaystyle \sum_{k=1}^n k^3\) の公式は \(\displaystyle \sum_{k=1}^n k\) の公式を \(2\) 乗した形なので覚えやすいですね。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n k^3 = \left\{ \frac{1}{2} n(n + 1) \right\}^2}\end{align}
先ほどの平方数の和と同様の考え方で証明できます(覚える必要はなし)。
\((k + 1)^4 = k^4 + 4k^3 + 6k^2 + 4k + 1\) より、
\((k + 1)^4 − k^4 = 4k^3 + 6k^2 + 4k + 1\) …①
①の恒等式の左辺および右辺の、\(k = 1, 2, \cdots, n\) の和を考えると、
(左辺の和)
\(\displaystyle = \sum_{k=1}^n \{(k + 1)^4 − k^4\}\)
\(\displaystyle = \sum_{k=1}^n (k + 1)^4 − \sum_{k=1}^n k^4\)
\(= \{2^4 + 3^4 + \cdots + (n + 1)^4\} \) \(−\, (1^4 + 2^4 + \cdots + n^4)\)
\(= (n + 1)^4 − 1^4\)
\(= (n + 1)^4 − 1\)
(右辺の和)
\(\displaystyle = \sum_{k=1}^n (4k^3 + 6k^2 + 4k + 1)\)
\(\displaystyle = 4\sum_{k=1}^n k^3 + 6\sum_{k=1}^n k^2 + 4\sum_{k=1}^n k + \sum_{k=1}^n 1\)
\(\displaystyle = 4\sum_{k=1}^n k^3 + 6 \cdot \frac{1}{6} n(n + 1)(2n + 1) \) \(\displaystyle + \,4 \cdot \frac{1}{2} n(n + 1) + n\)
\(\displaystyle = 4\sum_{k=1}^n k^3 + n(n + 1)(2n + 1) \) \(+ \,2n(n + 1) + n\)
(左辺の和) = (右辺の和) より、
\(\displaystyle (n + 1)^4 − 1 = \) \(\displaystyle 4\sum_{k=1}^n k^3 + n(n + 1)(2n + 1) + 2n(n + 1) + n\)
よって
\(\displaystyle \sum_{k=1}^n k^3\)
\(\displaystyle = \frac{1}{4} \{(n + 1)^4 − 1 − n(n + 1)(2n + 1) \) \(\displaystyle−\, 2n(n + 1) − n\}\)
\(\displaystyle = \frac{1}{4} \{(n + 1)^4 − n(n + 1)(2n + 1) \) \(\displaystyle−\, 2n(n + 1) − (n + 1)\}\)
\(\displaystyle = \frac{1}{4} (n + 1)\{(n + 1)^3 − n(2n + 1) − 2n − 1\}\)
\(\displaystyle = \frac{1}{4} (n + 1)\{(n + 1)^3 − (2n^2 + 3n + 1)\}\)
\(\displaystyle = \frac{1}{4} (n + 1)\{(n + 1)^3 − (2n + 1)(n + 1)\}\)
\(\displaystyle = \frac{1}{4} (n + 1)^2 \{(n + 1)^2 − (2n + 1)\}\)
\(\displaystyle = \frac{1}{4} (n + 1)^2 (n^2 + 2n + 1 − 2n − 1)\)
\(\displaystyle = \frac{1}{4} (n + 1)^2 n^2\)
\(\displaystyle = \left\{ \frac{1}{2} n(n + 1) \right\}^2\)
(証明終わり)
公式④の計算上の注意点
計算上の注意点は、公式② \(\displaystyle \sum_{k=1}^n k\) と同じです。
(例)
\(\begin{align}\displaystyle \sum_{k=1}^n 5k^3 &= 5\sum_{k=1}^n k^3\\&= 5 \left\{ \frac{1}{2} n(n + 1) \right\}^2\\&= \color{red}{\frac{5}{4} n^2(n + 1)^2}\end{align}\)
\(\displaystyle \sum_{k=1}^{n−1} k^3 = \color{red}{\left\{ \frac{1}{2} (n − 1)n \right\}^2}\)
【公式⑤】等比数列の和
指数に変数を含むものは、等比数列を思い出しましょう。
\begin{align}\color{red}{\displaystyle \sum_{k=1}^n ar^{k−1} = \frac{a(1 − r^n)}{1 − r} = \frac{a(r^n − 1)}{r − 1}}\end{align}
(\(r\) は \(k\) に無関係な定数、ただし \(r \neq 1\))
展開してみると等比数列の和を求めていることがわかります。
 等比数列をわかりやすく解説!一般項や等比数列の和の公式
等比数列をわかりやすく解説!一般項や等比数列の和の公式
\(\displaystyle \sum_{k=1}^n ar^{k−1}\)
\(= ar^0 + ar^1 + ar^2 + \cdots + ar^{n−1}\)
\(= a + ar + ar^2 + \cdots + ar^{n−1}\)
これは初項 \(a\)、公比 \(r\) の等比数列の和であるから、
\(\displaystyle \sum_{k=1}^n r^{k−1} = \frac{a(1 − r^n)}{1 − r}\)
(証明終わり)
公式⑤の計算上の注意点
等比数列の和では、必ず初項、公比、項数を意識しましょう。
(例)
\(\begin{align}\displaystyle \sum_{k=1}^n r^k &= \sum_{k=1}^n r \cdot r^{k−1} \\&= \frac{r(1 − r^n)}{1 − r} \\&= \color{red}{\frac{r(r^n − 1)}{r − 1}}\end{align}\)
(初項 \(r\)、公比 \(r\)、項数 \(n\))(\(r \neq 1\))
\(\begin{align}\displaystyle \sum_{k=1}^{n−1} 3 \cdot 2^{k−1} &= \frac{3(2^{n−1} − 1)}{2 − 1}\\&= \color{red}{3(2^{n−1} − 1)}\end{align}\)
(初項 \(3\)、公比 \(2\)、項数 \(n − 1\))
シグマ \(\sum\) の計算問題
最後に、計算問題に挑戦しましょう。
計算問題①「和を \(\sum\) で表す」
まずは、\(\sum\) の意味を確認する問題です。
(1) \(\displaystyle \sum_{k=1}^5 (2k + 3)\) を具体的な値の和の式で表せ。
(2) \(1 \cdot 1^2 + 3 \cdot 2^2 + 5 \cdot 3^2 + 7 \cdot 4^2 + 9 \cdot 5^2\) を \(\sum\) を用いて表せ。

(1) では、条件式の変数 \(k\) の部分に、はじめの値から終わりの値まで順に代入し、足せば良いですね。
また、(2) のような問題では、一般項(第 \(k\) 項)がどんな形になるかをまず考えましょう。
(1)
\(\displaystyle \sum_{k=1}^5 (2k + 3)\)
\(= (2 \cdot 1 + 3) + (2 \cdot 2 + 3) + (2 \cdot 3 + 3) \) \(+\, (2 \cdot 4 + 3) + (2 \cdot 5 + 3)\)
\(= 5 + 7 + 9 + 11 + 13\)
答え: \(\color{red}{5 + 7 + 9 + 11 + 13}\)
(2)
数列 \(1 \cdot 1^2\), \(3 \cdot 2^2\), \(5 \cdot 3^2\), \(7 \cdot 4^2\), \(9 \cdot 5^2\)
の第 \(k\) 項は \((2k − 1)k^2\) であるから、
\(1 \cdot 1^2 + 3 \cdot 2^2 + 5 \cdot 3^2 + 7 \cdot 4^2 + 9 \cdot 5^2\) \(\displaystyle = \sum_{k=1}^5 (2k − 1)k^2\)
答え: \(\color{red}{\displaystyle \sum_{k=1}^5 (2k − 1)k^2}\)
計算問題②「\(\sum\) 計算」
続いて、\(\sum\) の公式を使った計算問題です。
次の和を求めよ。
(1) \(\displaystyle \sum_{k=1}^n (2k^2 − k + 7)\)
(2) \(\displaystyle \sum_{k=5}^{n−1} (4k + 3)\)

\(\sum\) 計算は、いかに楽できるかが勝負です。
共通の係数や項はすぐにくくって、展開を最小限にしましょう。
また、\(k = 1 \sim n\) 以外のときは、展開と代入のプロセスを分けるとミスが減りますよ。
(1)
\(\displaystyle \sum_{k=1}^n (2k^2 − k + 7)\)
\(\displaystyle = 2\sum_{k=1}^n k^2 − \sum_{k=1}^n k + \sum_{k=1}^n 7\)
\(\displaystyle = \frac{2}{6} n(n + 1)(2n + 1) − \frac{1}{2} n(n + 1) + 7n\)
\(\displaystyle = \frac{1}{6} n\{2(n + 1)(2n + 1) − 3(n + 1) + 42\}\)
\(\displaystyle = \frac{1}{6} n(4n^2 + 6n + 2 − 3n − 3 + 42)\)
\(\displaystyle = \frac{1}{6} n(4n^2 + 3n + 41)\)
答え: \(\color{red}{\displaystyle \frac{1}{6} n(4n^2 + 3n + 41)}\)
(2)
\(\displaystyle \sum_{k=1}^n (4k + 3)\)
\(\displaystyle = 4\sum_{k=1}^n k + \sum_{k=1}^n 3\)
\(\displaystyle = 4 \cdot \frac{1}{2} n(n + 1) + 3n\)
\(= n\{2(n + 1) + 3\}\)
\(= n(2n + 5)\)
より、
\(\displaystyle \sum_{k=5}^{n−1} (4k + 3)\)
\(\displaystyle = \sum_{k=1}^{n−1} (4k + 3) − \sum_{k=1}^4 (4k + 3)\)
\(= (n − 1)\{2(n − 1) + 5\} − 4(2 \cdot 4 + 5)\)
\(= (n − 1)(2n + 3) − 52\)
\(= 2n^2 + n − 3 − 52\)
\(= 2n^2 + n − 55\)
\(= (2n + 11)(n − 5)\)
答え: \(\color{red}{(2n + 11)(n − 5)}\)
計算問題③「少し複雑な \(\sum\) 計算」
ここまでできれば、\(\sum\) への理解はバッチリです!
次の和を求めよ。
(1) \(\displaystyle \sum_{i=1}^n (2^i − 1)\)
(2) \(\displaystyle \sum_{m=1}^n \left( \sum_{k=1}^m k \right)\)
(3) \(1^2 \cdot n + 2^2 \cdot (n−1) + 3^2 \cdot (n−2) \,+ \) \(\cdots + (n−1)^2 \cdot 2 + n^2 \cdot 1\)

変数の文字が違っても、根本的な意味は変わりません。
(3) では、\(\sum\) 計算に関係する部分、しない部分を見極めましょう。
(1)
\(\displaystyle \sum_{i=1}^n (2^i − 1)\)
\(\displaystyle = \sum_{i=1}^n 2^i − \sum_{i=1}^n 1\)
\(\displaystyle = \frac{2(2^n − 1)}{2 − 1} − n\)
\(= 2^{n+1} − n − 2\)
答え: \(\color{red}{2^{n+1} − n − 2}\)
(2)
\(\displaystyle \sum_{m=1}^n \left( \sum_{k=1}^m k \right)\)
\(\displaystyle = \sum_{m=1}^n \left\{ \frac{1}{2} m(m + 1) \right\}\)
\(\displaystyle = \frac{1}{2} \sum_{m=1}^n (m^2 + m)\)
\(\displaystyle = \frac{1}{2} \left( \sum_{m=1}^n m^2 + \sum_{m=1}^n m \right)\)
\(\displaystyle = \frac{1}{2} \left\{ \frac{1}{6} n(n + 1)(2n + 1) + \frac{1}{2} n(n + 1)\right\}\)
\(\displaystyle = \frac{1}{2} \cdot \frac{1}{6} n(n + 1)\{(2n + 1) + 3\}\)
\(\displaystyle = \frac{1}{12} n(n + 1)(2n + 4)\)
\(\displaystyle = \frac{1}{6} n(n + 1)(n + 2)\)
答え: \(\color{red}{\displaystyle \frac{1}{6} n(n + 1)(n + 2)}\)
(3)
数列 \(1^2 \cdot n\), \(2^2 \cdot (n−1)\), \(3^2 \cdot (n−2)\), \(\cdots\), \((n−1)^2 \cdot 2\), \(n^2 \cdot 1\)
の第 \(k\) 項は \(k^2 \cdot \{n − (k − 1)\} = k^2(n − k + 1)\)
また、項数は \(n\) であるから、
\(1^2 \cdot n + 2^2 \cdot (n−1) + 3^2 \cdot (n−2)\, + \) \(\cdots + (n−1)^2 \cdot 2 + n^2 \cdot 1\)
\(\displaystyle = \sum_{k=1}^n k^2(n − k + 1)\)
\(\displaystyle = \sum_{k=1}^n \{k^2(n + 1) − k^3\}\)
\(\displaystyle = (n + 1)\sum_{k=1}^n k^2 − \sum_{k=1}^n k^3\)
\(\displaystyle = \frac{1}{6} n(n + 1)^2(2n + 1) − \frac{1}{4} n^2(n + 1)^2\)
\(\displaystyle = \frac{1}{12} n(n + 1)^2 \{2(2n + 1) − 3n\}\)
\(\displaystyle = \frac{1}{12} n(n + 1)^2(n + 2)\)
答え: \(\color{red}{\displaystyle \frac{1}{12} n(n + 1)^2(n + 2)}\)
以上で問題も終わりです。
複雑な計算に見えるシグマ \(\sum\) ですが、規則的な数の総和を表すのにとても便利な道具です。
記号の意味や計算公式をしっかり理解して、ぜひマスターしてくださいね!
