この記事では、「等差数列」についてどこよりもわかりやすく解説していきます。
等差数列の一般項や和の公式の覚え方と使い方、計算問題の解き方を説明していくので、この記事を通してぜひ等差数列を得点源にしてくださいね!
目次
等差数列とは?
等差数列とは、はじめの数にある一定の数を足し続ける数列のことです。
隣り合う数が等しい差をもつから、「等差数列」と呼ぶのですね。
例えば、正の奇数を小さいものから順に並べた数列
\(1, 3, 5, 7, 9, 11, 13,\) …
は、「はじめの数 \(1\) に一定の数 \(2\) を足し続ける」ので等差数列です。
このとき、等差数列のはじめの数を「初項」、足し続ける一定の数を「公差」と呼びます。
したがって、この数列は「初項 \(1\)、公差 \(2\) の等差数列」と表現できます。
等差数列の一般項
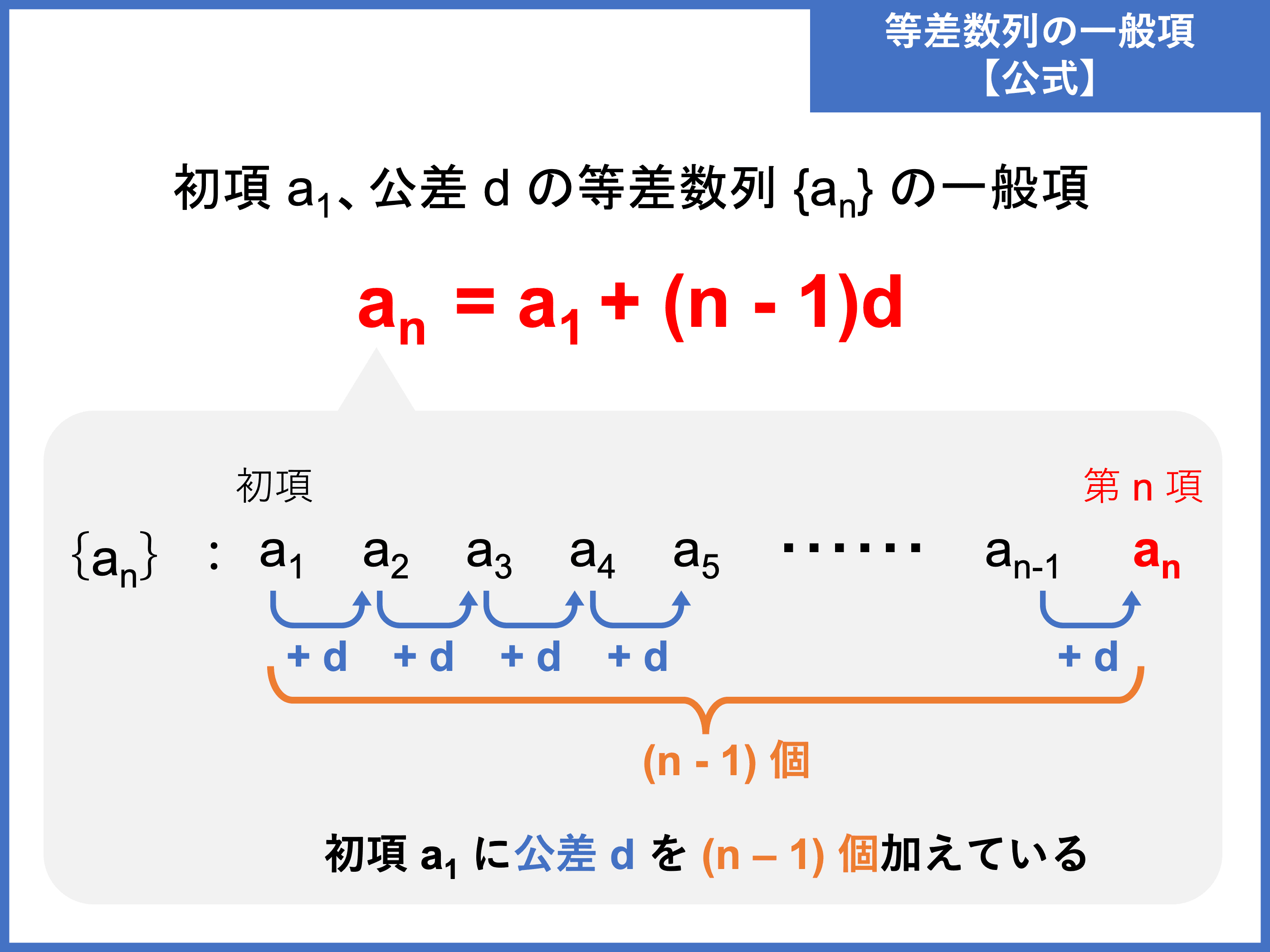
等差数列の一般項は次のように表されます。
初項 \(a\)、公差 \(d\) である等差数列 \(\{a_n\}\) の一般項 \(a_n\) は
\begin{align}\color{red}{a_n = a + (n − 1)d}\end{align}
一般項
規則性をもつ数列の任意の項を一般化した式(第 \(n\) 項の値)。
等差数列の一般項の覚え方
等差数列の一般項の公式を覚えるには、一般項の成り立ちを理解するのが一番です。
初項が \(a\)、公差が \(d\) である等差数列 \(\{a_n\}\) を第 \(1\) 項から並べていくと、
\(a_1 = a\)
\(a_2 = a + d\)
\(a_3 = a + 2d\)
\(a_4 = a + 3d\)
…
初項 \(a\) に公差 \(d\) を足していくので、第 \(2\) 項には 公差 \(1\) つ分、第 \(3\) 項には公差 \(2\) つ分と、\((\text{項数} − 1)\) 個の公差 \(d\) が足されていきます。
したがって、第 \(n\) 項は「\(\color{red}{a_n = a + (n − 1)d}\)」と表すことができるのです。
公式を覚えるのが苦手な人は、毎回このように一般項を自分で導く訓練を積みましょう。
そうすれば、自然と一般項を覚えられるようになりますよ!
例題「等差数列の一般項の求め方」
例題を通して、等差数列の一般項を求める手順を説明します。
第 \(15\) 項が \(33\)、第 \(45\) 項が \(153\) である等差数列の一般項を求めよ。
等差数列の一般項は、初項 \(a\) と公差 \(d\) さえわかれば求められます。
まずは求める数列の一般項を数式として表します。
問題文に初項と公差が書かれていない場合は、自分で \(a\), \(d\) という文字でおきます。
この数列の初項を \(a\)、公差を \(d\) とおくと、一般項 \(a_n\) は以下のように書ける。
\(a_n = a + (n − 1)d\) …(*)
問題文にある項(第 \(15\) 項と第 \(45\) 項)を一般項の式で表し、連立方程式を得ます。
その連立方程式を解いて、初項 \(a\) と公差 \(d\) を求めます。
\(a_{15} = 33\)、\(a_{45} = 153\) であるから、(*) より
\(\left\{\begin{array}{l}33 = a + 14d …①\\153 = a + 44d …②\end{array}\right.\)
② − ① より、
\(120 = 30d\)
\(d = 4\)
① より
\(\begin{align}a &= 33 − 14d\\&= 33 − 14 \cdot 4\\&= 33 − 56\\&= − 23\end{align}\)
最後に、求めた初項 \(a\) と公差 \(d\) の値を最初の式に代入すれば、一般項の完成です!
(*) に \(a = − 23\), \(d = 4\) を代入して、
\(\begin{align}a_n &= − 23 + 4(n − 1)\\&= − 23 + 4n − 4\\&= 4n − 27\end{align}\)
答え: \(a_n = 4n − 27\)
等差数列の和の公式
等差数列の和には次の \(2\) 通りの公式があります。
- 初項と末項から求める
初項 \(a\)、末項 \(l\)、項数 \(n\) の等差数列の和 \(S_n\) は
\begin{align}\color{red}{S_n = \displaystyle \frac{1}{2}n(a + l)}\end{align} - 初項と公差から求める
初項 \(a\)、公差 \(d\)、項数 \(n\) の等差数列の和 \(S_n\) は
\begin{align}\color{red}{S_n = \displaystyle \frac{1}{2}n\{2a + (n − 1)d\}}\end{align}
上記公式を使って、等差数列 \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\) の和 \(S_{10}\) を求めてみましょう。
数列 \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\) は
初項 \(1\)、末項 \(10\)、項数 \(10\) の等差数列であるから
\(\begin{align}S_{10} &= \displaystyle \frac{1}{2} \cdot 10(1 + 10)\\&= \displaystyle \frac{1}{2} \cdot 10 \cdot 11\\&= \color{red}{55}\end{align}\)
数列 \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\) は
初項 \(1\)、公差 \(1\)、項数 \(10\) の等差数列であるから
\(\begin{align}S_{10} &= \displaystyle \frac{1}{2} \cdot 10\{2 \cdot 1 + (10 − 1) \cdot 1\}\\&= \displaystyle \frac{1}{2} \cdot 10 \cdot 11\\&= \color{red}{55}\end{align}\)
この数列の和を単純な足し算で求めると、確かに \(55\) になりますね。
\(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10\) \(= \color{red}{55}\)
\(10\) 項程度であればこのように足して求めるのも苦ではないかもしれませんが、\(20\) 項、\(100\) 項と項数が増えると書き出すだけでも大変です。
ですので、等差数列の和の公式は必ず覚えておきましょう!
等差数列の和の公式の覚え方
等差数列の和の公式を覚えるにも、やはり公式の成り立ちを理解するのが一番です。
初項が \(a\)、末項が \(l\)、公差が \(d\)、項数が \(n\) である等差数列 \(\{a_n\}\) の和 \(S_n\) を考えます。
\(S_n\) を \(a_1\) 〜 \(a_n\) の順に並べたものと、順序を逆にして \(a_n\) 〜 \(a_1\) の順に並べたものを足し合わせて \(2\) で割ると、等差数列の和の公式①「\(\color{red}{S_n = \displaystyle \frac{1}{2}n(a + l)}\)」が得られます。

また、末項 \(l\) は第 \(n\) 項なので、\(l = a + (n − 1)d\) とも表せます(一般項と同じ式)。
これを①に代入すると、公式②「\(\color{red}{S_n = \displaystyle \frac{1}{2}n\{2a + (n − 1)d\}}\)」が得られます。
\(\begin{align}S_n &= \displaystyle \frac{1}{2}n(a + \color{salmon}{l})\\&= \displaystyle \frac{1}{2}n\{a + \color{salmon}{a + (n − 1)d}\}\\&= \color{red}{\displaystyle \frac{1}{2}n\{2a + (n − 1)d\}}\end{align}\)
公式①と②は、出題形式によって使い分けが必要です。
どちらも覚えるのが難しい人は、公式①「\(S_n = \displaystyle \frac{1}{2}n(a + l)\)」を優先的に覚えてください。
末項 \(l\) は第 \(n\) 項なので、毎回、一般項 \(a_n\) のかたちを求めてから代入すれば問題ありません。
例題「等差数列の和の求め方」
例題を通して、等差数列の和の求め方を説明します。
初項 \(20\)、公差 \(− 3\) の等差数列において、初項からある項までの和が初めて負となるときの項数が第何項になるかを求めよ。また、そのときの和を求めよ。
等差数列の和ときたら、必要なものは「初項」「末項 or 公差」「項数」です。
問題文からわかるもの、わからないものを識別して、等差数列の和を式で表すのがポイントです。
等差数列の和の公式を利用して、求める和 \(S_n\) を数式で表します。
この例題では「初項」と「公差」が出てきているので、公式② \(S_n = \displaystyle \frac{1}{2}n\{2a + (n − 1)d\}\) が使えます。
「項数」がまだわからないので、\(n\) とおいておきます。
この等差数列を \(\{a_n\}\) とおき、求める項数を第 \(n\) 項とする。
数列 \(\{a_n\}\) の初項から第 \(n\) 項までの和 \(S_n\) は、
初項 \(20\)、公差 \(− 3\)、項数 \(n\) より、
\(\begin{align}S_n &= \displaystyle \frac{1}{2}n\{2 \cdot 20 + (n − 1)(−3)\}\\&= \displaystyle \frac{1}{2}n(40 − 3n + 3) \\&= \displaystyle \frac{1}{2}n(43 − 3n)\end{align}\)
一般項 \(a_n\) を求めてから和の公式①「\(S_n = \displaystyle \frac{1}{2}n(a + l)\)」を使ってもOKです。
(別解)
初項 \(20\)、公差 \(− 3\) より、一般項 \(a_n\) は
\(\begin{align}a_n &= 20 + (n − 1)(− 3)\\&= 20 − 3n + 3\\&= − 3n + 23\end{align}\)
初項から第 \(n\) 項までの和 \(S_n\) は、
初項 \(20\)、末項 \(−3n + 23\)、項数 \(n\) より、
\(\begin{align}S_n &= \displaystyle \frac{1}{2}n\{20 + (−3 n + 23)\}\\&= \displaystyle \frac{1}{2}n(43 − 3n)\end{align}\)
問題文の条件から、わかっていない値を求めます。
この例題では、和が負になるときの項数 \(n\) の値を不等式を立てて求めればよいですね。
\(S_n\) が負となるとき、
\(\displaystyle \frac{1}{2}n(43 − 3n) < 0\)
\(n\) は自然数 \((n > 0)\) であるから、
\(43 − 3n < 0\)
\(43 < 3n\)
\(3n > 43\)
\(n > \displaystyle \frac{43}{3} = 14.33\)… より
\(n \geq 15\)
したがって、初項から第 \(15\) 項までの和が初めて負となる。
最後に、STEP.1 で立てた和の式に求めた値を代入すれば、答えが求められます!
したがって、そのときの和 \(S_{15}\) は
\(\begin{align}S_{15} &= \displaystyle \frac{1}{2} \cdot 15 \cdot (43 − 3 \cdot 15)\\&= \displaystyle \frac{1}{2} \cdot 15 \cdot (− 2)\\&= − 15\end{align}\)
答え: 第 \(15\) 項、和は \(− 15\)
等差数列の性質
等差数列には、\(2\) つの重要な性質があります。
性質① 公差が一定
等差数列には、どの \(2\) 項間の差も等しいという性質があります。
これは等差数列の定義そのものですね。
等差数列 \(\{a_n\}\) の公差が \(d\) のとき、すべての自然数 \(n\) について次の関係が成り立つ。
\begin{align}a_{n + 1} = a_n + d\end{align}
すなわち
\begin{align}\color{red}{a_{n + 1} − a_n = d}\end{align}
このように、数列の規則性を隣り合う項の関係式で表したものを「漸化式」といいます。
 漸化式とは?基本型や特性方程式をわかりやすく解説!
漸化式とは?基本型や特性方程式をわかりやすく解説!
性質② 等差中項
等差数列の連続する \(3\) 項において、両端の項の和は真ん中の項の \(2\) 倍に等しいという性質があります。
このとき、真ん中の項 \(b\) を「\(a\) と \(c\) の等差中項」といいます。
\(3\) つの数 \(a, b, c\) がこの順で等差数列を成すとき、以下の等式が成り立つ。
\begin{align}\color{red}{2b = a + c}\end{align}
等差中項の関係式は、等差数列の定義から導けます。
数列 \(a, b, c\) の公差を \(d\) とおくと、
\(d = b − a、d = c − b\)
であるから、
\(b − a = c − b\)
したがって、
\(\color{red}{2b = a + c}\) が成り立つ。
これら \(2\) つの性質は、問題を解くための道具として使うことができます。
「あともう \(1\) つ条件式があれば…」という場面で力を発揮してくれるので、しっかり理解しておきましょう。
等差数列の計算問題
等差数列の勉強の仕上げに、計算問題を \(3\) 題解いてみましょう!
計算問題①「等差数列と調和数列」
数列 \(\{a_n\}\) について、各項の逆数を項とする数列 \(\displaystyle \frac{1}{a_1}, \displaystyle \frac{1}{a_2}, \displaystyle \frac{1}{a_3},\) … が等差数列になるとき、もとの数列 \(\{a_n\}\) を調和数列という。
例えば、数列 \(1, \displaystyle \frac{1}{2}, \displaystyle \frac{1}{3}, \displaystyle \frac{1}{4},\) … は調和数列である。
このことを踏まえ、調和数列 \(20, 15, 12, 10,\) … の一般項 \(a_n\) を求めよ。

大学の入試問題では、問題文の冒頭で見慣れない単語の定義を説明し、受験生にそれを理解させた上で解かせる問題が、少なからず存在します。
こういった場合は、あわてず、問題の意味をしっかり理解した上で解きましょう!
\(\{a_n\} = 20, 15, 12, 10, \cdots \) が調和数列であることから、
\(\left\{\displaystyle \frac{1}{a_n}\right\} = \displaystyle \frac{1}{20}, \displaystyle \frac{1}{15}, \displaystyle \frac{1}{12}, \displaystyle \frac{1}{10},\) … が等差数列となる。
数列 \(\left\{\displaystyle \frac{1}{a_n}\right\}\) の初項は \(\displaystyle \frac{1}{20}\)、
公差は
\(\displaystyle \frac{1}{15} − \displaystyle \frac{1}{20} = \displaystyle \frac{4 − 3}{60} = \displaystyle \frac{1}{60}\)
であるから、
一般項 \(\displaystyle \frac{1}{a_n}\) は
\(\begin{align}\displaystyle \frac{1}{a_n} &= \displaystyle \frac{1}{20} + (n − 1) \cdot \displaystyle \frac{1}{60}\\\\&= \displaystyle \frac{3 + n − 1}{60}\\\\&= \displaystyle \frac{n + 2}{60}\end{align}\)
\(n\) は自然数なので、\(n + 2 > 0\) であるから、\(\displaystyle \frac{1}{a_n}\) の逆数をとって
\(a_n = \displaystyle \frac{60}{n + 2}\)
したがって、調和数列の一般項は
\(a_n = \displaystyle \frac{60}{n + 2}\)
答え: \(a_n = \displaystyle \frac{60}{n + 2}\)
計算問題②「等差数列の和の最大値を求める」
初項 \(77\)、公差 \(− 4\) の等差数列について、和の最大値を求めよ。

公差がマイナスの数なので、項数が増えるごとに項は小さくなります。
そのため、あるところまでは数列の和が増えていきますが、項がマイナスの数になったところから数列の和が減少していくはずです。
これをうまく言葉と数式で表現してみましょう。
等差数列を \(\{a_n\}\) とおくと、
\(\begin{align}a_n &= 77 + (n − 1) \cdot (− 4)\\&= 77 − 4n + 4\\&= − 4n + 81\end{align}\)
この等差数列の和が最大となる条件は、初項から順に項を加えていったときに、最後の項が正の数で、その次の項が負の数になることである。
すなわち、和が最大となるときの項を第 \(n\) 項とすると、
\(− 4n + 81 > 0\)
となればよい。
\(− 4n > − 81\)
よって
\(n < \displaystyle \frac{81}{4} \leq 20\)
したがって、初項から第 \(20\) 項までの和が最大となる。
初項 \(77\)、公差 \(−4\)、項数 \(20\) より、求める最大値 \(S_{20}\) は
\(\begin{align}S_{20} &= \displaystyle \frac{1}{2} \cdot 20\{2 \cdot 77 + (20 − 1) \cdot (− 4)\}\\&= 10(154 − 76)\\&= 10 \cdot 78\\&= 780\end{align}\)
答え: \(780\)
計算問題③「等差数列をなす 3 数を求める」
等差数列を成す \(3\) 数があり、その和が \(45\)、積が \(3240\) であるとき、その \(3\) 数を求めよ。

「等差数列」「\(3\) 数」ときたら、等差中項を思い出しましょう。
問題文にある条件と等差中項から、\(3\) 数のうちの \(1\) つが求められます。
あとの \(2\) 数を求めるときには、「解と係数の関係」を逆に利用できます。
\(\alpha, \beta\) に関する連立方程式
\begin{align}\left\{\begin{array}{l}\alpha + \beta = −a\\\alpha\beta= b\end{array}\right.\end{align}
の解は、二次方程式 \(x^2 + ax + b = 0\) の \(2\) つの解である。
等差数列を成す \(3\) 数を \(a, b, c \ (a < b < c)\) とおく。
和が \(45\)、積が \(3240\) であるから、
\(\left\{\begin{array}{l}a + b + c = 45 …①\\abc = 3240 …②\end{array}\right.\)
また、等差中項より
\(2b = a + c …③\)
③ を ① に代入して、
\(3b = 45\)
\(b = 15\)
①、② に戻して整理すると、
\(\left\{\begin{array}{l}a + c = 30 …①’\\ac = 216 …②’\end{array}\right.\)
解と係数の関係より、\(a\) と \(c\) は \(x\) に関する二次方程式 \(x^2 – 30x + 216 = 0\) の \(2\) 解であることがわかる。
因数分解して、
\((x − 12)(x − 18) = 0\)
\(x = 12, 18\)
\(a < c\) より、
\(a = 12、c = 18\)
以上より、求める \(3\) 数は \(12, 15, 18\) である。
答え: \(12, 15, 18\)
以上で、計算問題も終わりです!
等差数列は、最も基本的な数列の \(1\) つです。
覚えることや問題のバリエーションが多く、大変に感じるかもしれませんが、等差数列の性質や公式の成り立ちを理解していれば、なんてことはありません。
ぜひ、等差数列をマスターしてくださいね!
「等比数列」「階差数列」など、ほかの数列について調べたい方は以下のまとめ記事から探してみてくださいね!
 数列を総まとめ!一般項・和・漸化式などの重要記事一覧
数列を総まとめ!一般項・和・漸化式などの重要記事一覧


とても分かりやすかったです。
小学生の娘でも理解できました!ありがとうございます。
文才があると思います!
この度はコメントいただきありがとうございます。
当サイト記事が家庭教育のお役に立てておりましたら何よりです。
今後ともどうぞ当サイトをよろしくお願いいたします。