この記事では、「導関数」と「微分係数」の違いをわかりやすく解説していきます。
それぞれの定義や求め方、計算問題の解き方も紹介していきますので、この記事を通してぜひマスターしてくださいね。
目次
導関数・微分係数とは?
導関数とは、ある関数のある点(瞬間)における変化率を表す関数です。
一方、微分係数とは、ある関数の特定の点(瞬間)における変化率の値です。
導関数と微分係数の違いを一言で言えば、「関数か定数か」です。
これだけでは、わかるようでなんだかよくわからないですよね。
「変化率」の意味と、微分係数・導関数の定義を確認しながら、理解を深めましょう。
【準備】平均変化率と変化率
導関数と微分係数は「変化率」であると説明しました。変化率を理解するために、まずは「平均変化率」を押さえましょう。
関数における平均変化率とは、\(x\) の変化量に対する \(y\) の変化量の割合のことです。
関数 \(y = f(x)\) において、\(x\) の変化量 \(b − a\) に対する \(y\) の変化量 \(f(b) − f(a)\) の割合を、\(x\) が \(a\) から \(b\) まで変化するときの「平均変化率」と呼ぶ。
\begin{align}\color{red}{\displaystyle \text{(平均変化率)} = \frac{f(b) − f(a)}{b − a}}\end{align}
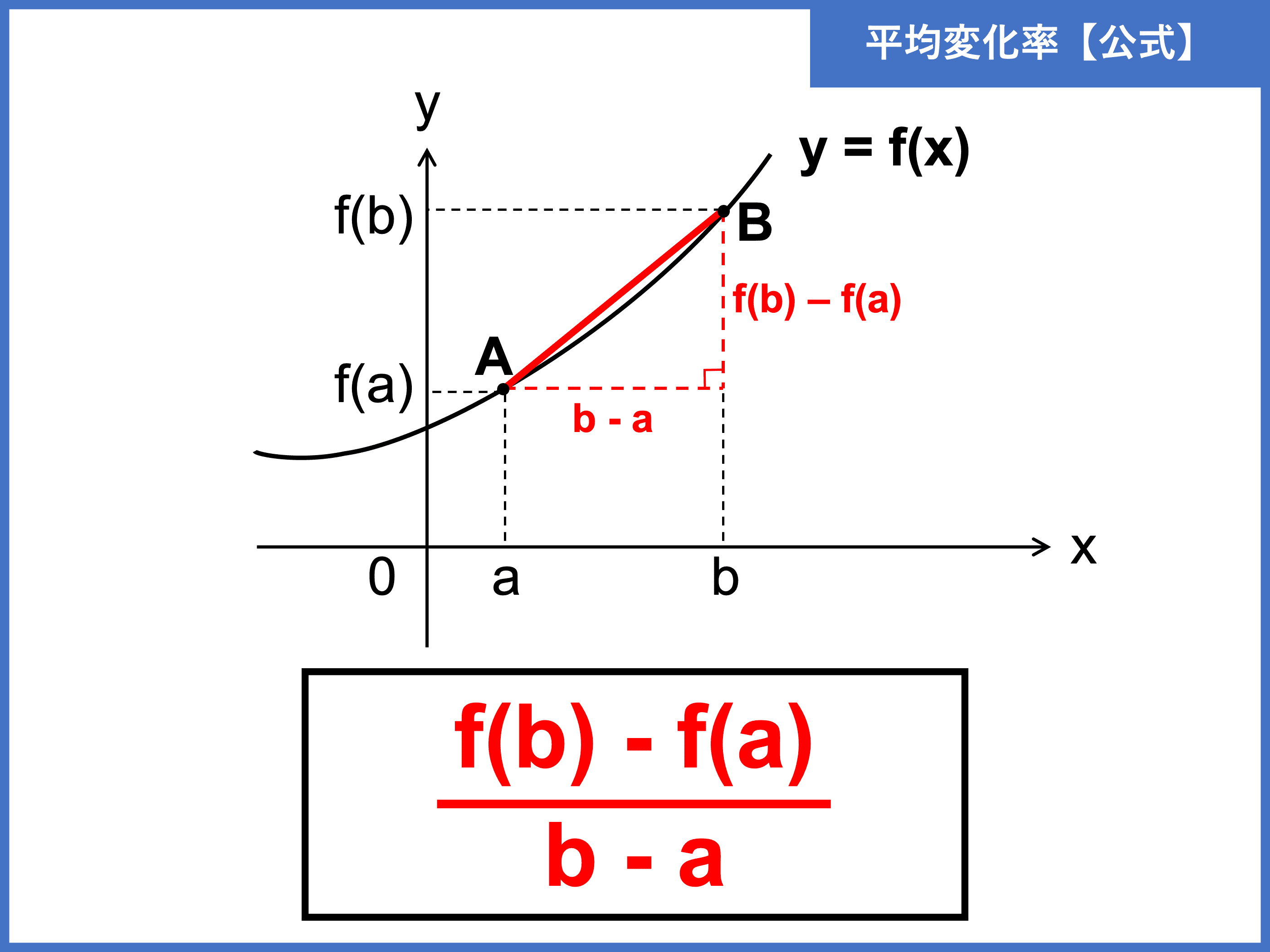
グラフ上で見れば、\(2\) 点間を結ぶ直線の傾きということですね。
実は、中学で習った「変化の割合」は平均変化率そのものです!
\begin{align}\color{red}{(\text{平均変化率})} \ &\color{red}{= (\text{変化の割合})} \\&\color{red}{= (\text{2 点間の傾き})}\end{align}
「平均」という言葉がつくのは、まさしく変化率の平均値を求めているからです。
本来の変化率は、\(x\) の位置によって刻々と変化しています。
グラフ上で見れば、ある点における接線の傾きがその点(瞬間)における変化率を表しているのです。
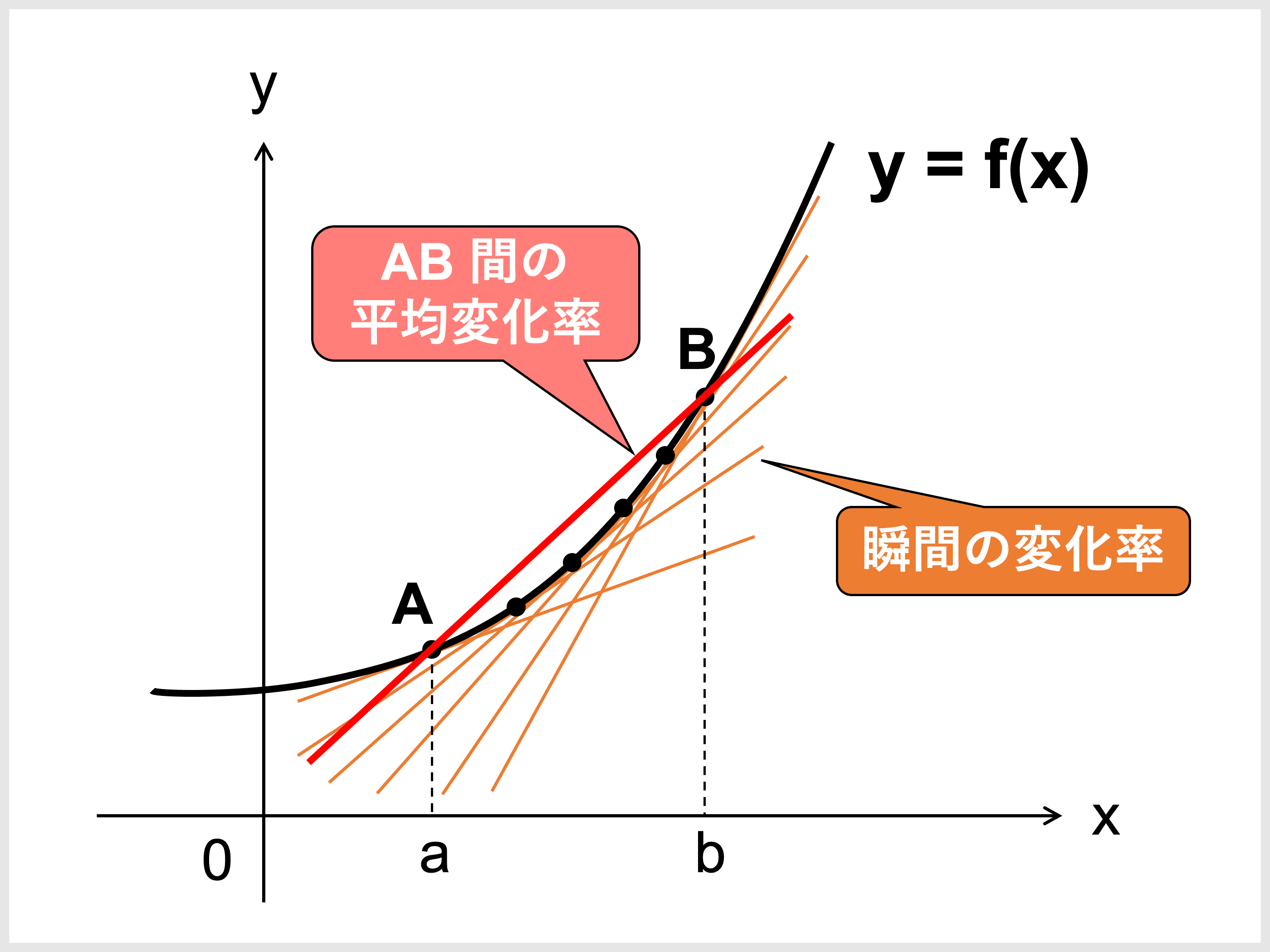
この接線の傾き(変化率)を求めるためには、「平均変化率における \(x\) の変化量を限りなく \(0\) に近づけて」いきます。

これを数式で表すことができれば、変化率を表せますね。
そこで、「極限値」という考え方を利用します。
関数 \(f(x)\) において、\(x\) が \(a\) と異なる値をとりながら \(a\) に限りなく近づくとき、\(f(x)\) がある一定の値 \(\alpha\) に限りなく近づく場合、この \(\alpha\) を「\(f(x)\) の極限値」といい、以下のように表す。
\begin{align}\color{red}{\displaystyle \lim_{x \to a} f(x) = \alpha}\end{align}
または
\(\color{red}{x \to a}\) のとき \(\color{red}{f(x) \to \alpha}\)
極限(limit)に近づくことを記号「\(\bf{\lim}\)」で表せるのですね。
これで準備が整いました。
いよいよ、微分係数と導関数の定義に入っていきましょう。
微分係数の定義
関数 \(y = f(x)\) において、特定の点 \((a, f(a))\) における瞬間の変化率(すなわち接線の傾き)のことを「微分係数」といい、「\(\color{red}{f’(a)}\)」と表します。
微分係数は、平均変化率の式において \(x\) の変化量を限りなく \(0\) に近づけることで求めることができます。
関数 \(f(x)\) の \(x = a\) における微分係数は、
\begin{align}\color{red}{\displaystyle f’(a) = \lim_{b \to a} \frac{f(b) − f(a)}{b − a}}\end{align}
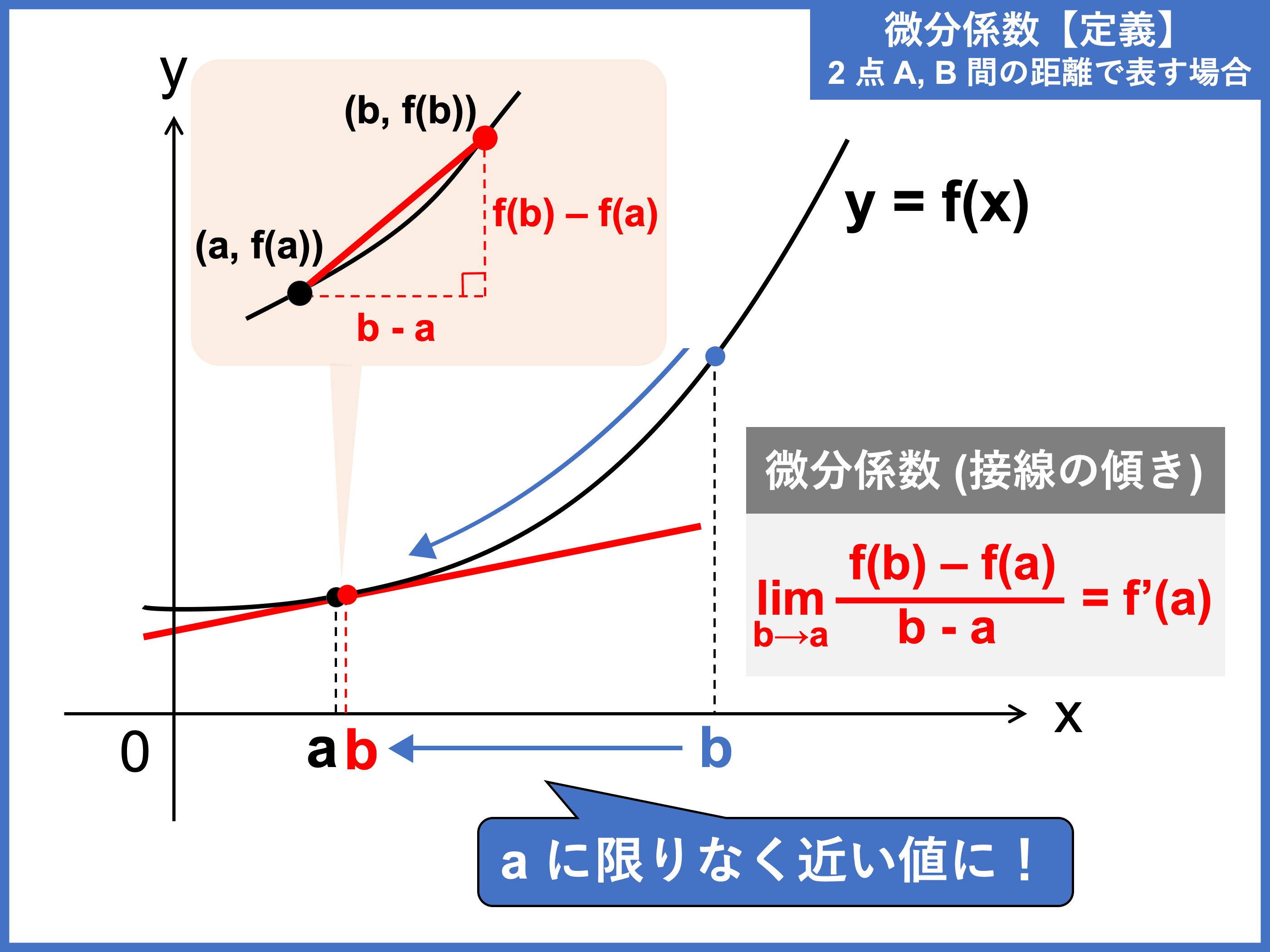
また、\(x\) の変化量を \(h\) とおくと、微分係数は以下のようにも表せる。
\begin{align}\color{red}{\displaystyle f’(a) = \lim_{h \to 0} \frac{f(a + h) − f(a)}{h}}\end{align}

変化量の表し方によって、\(2\) 通りの書き方ができるのですね。
微分係数は、個々の点における接線の傾きなので、点の位置によってどんどん変化するものです。
いろんな点における微分係数を求めようと思うと、各点において上記の式を作る必要があり大変です。
そこで、微分係数の式を一般化することにしました。それが「導関数」です。
導関数の定義
関数 \(y = f(x)\) において、ある点における瞬間の変化率(すなわち接線の傾き)を求められる関数を「導関数」といい、「\(\color{red}{f’(x)}\)」と表します。
点の \(x\) 座標さえ代入すれば微分係数を求められる、マシーンのようなものです。
関数 \(f(x)\) の導関数 \(f’(x)\) の定義は、
\begin{align}\color{red}{\displaystyle f’(x) = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}}\end{align}
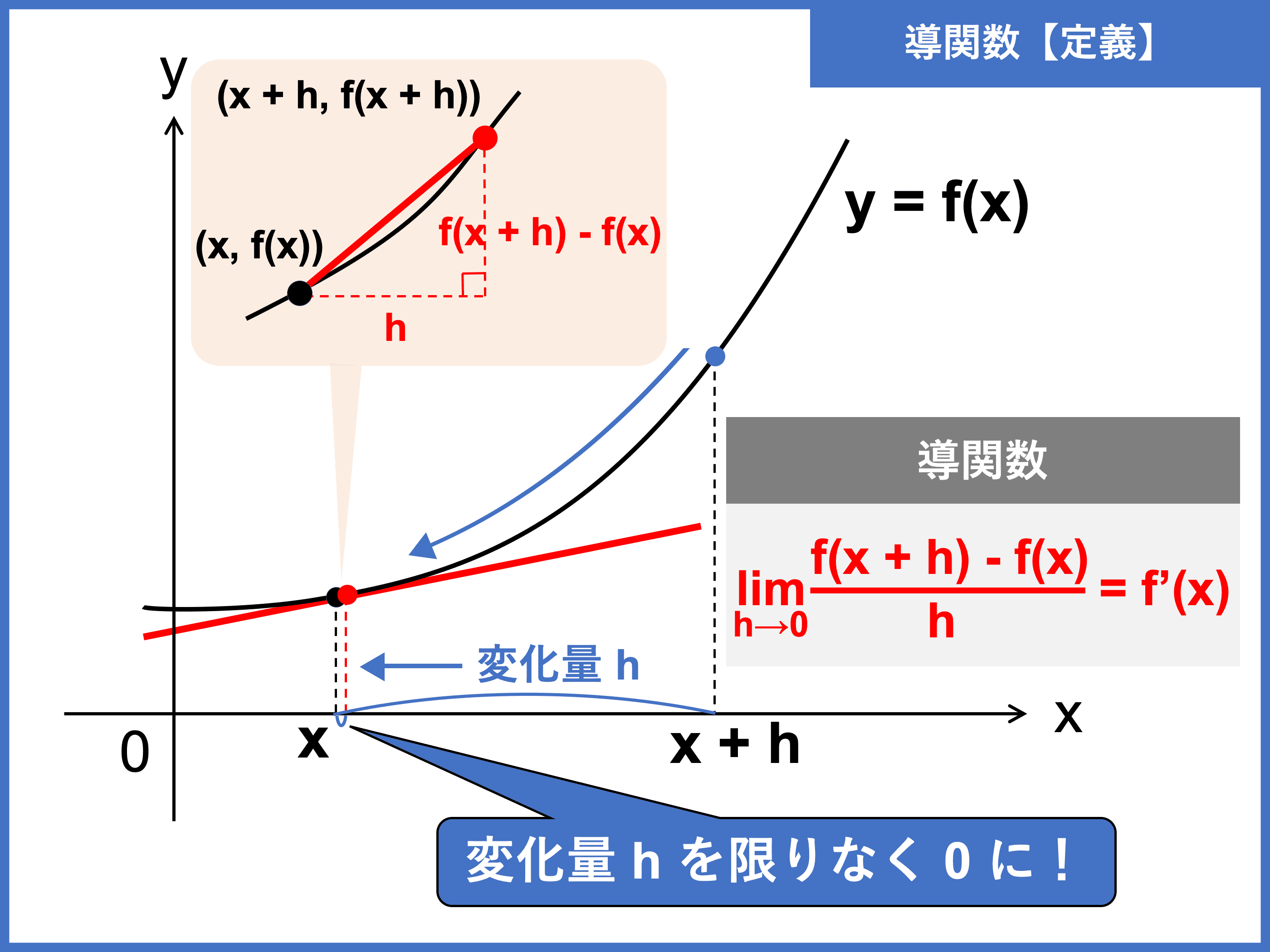
そして、関数 \(f(x)\) から導関数 \(f’(x)\) を求めることを「\(f(x)\) を微分する」という。
導関数の定義式をよく見ると、微分係数の定義式で \(x\) に特定の値を入れずに一般化しただけですね。
「導関数を求める = 微分する」ということは、必ず押さえておきましょう。
【参考】n 次導関数とは?
ある関数 \(f(x)\) の導関数は「一次導関数」、さらにその導関数は「二次導関数」、さらにその導関数は「三次導関数」…と呼んでいきます。
これらを総称して、「高次導関数(\(n\) 次導関数)」といいます。
関数 \(y = f(x)\) に対して、\(n\) 回微分してできる関数を「\(n\) 次導関数」といい、
\begin{align}\color{red}{y^{(n)} = f^{(n)}(x)}\end{align}
と表すことができる。
微分の回数を「階」で表すこともあり、その場合「\(n\) 階導関数」と呼びます。
なお、\(n\) が小さいときは
- \(y^{(1)} → \color{red}{y^{\prime}}\) または \(\color{red}{f^{\prime}(x)}\)
- \(y^{(2)} → \color{red}{y^{\prime\prime}}\) または \(\color{red}{f^{\prime\prime}(x)}\)
- \(y^{(3)} → \color{red}{y^{\prime\prime\prime}}\) または \(\color{red}{f^{\prime\prime\prime}(x)}\)
などと簡略化してダッシュ記号で表すことが多いです。
導関数の求め方
導関数は、問題での聞かれ方によって次の \(2\) 通りの求め方があります。
- 問題文に「導関数の定義にしたがって」とある場合
→ ① 導関数の定義から求める - 問題文に特に指示がない場合
→ ② 微分公式を使って求める
それぞれの求め方を同じ例題で説明します。
① 導関数の定義から求める
導関数の定義にしたがって、次の関数の導関数を求めよ。
\(y = x^2 − 3x + 9\)
問題文に「定義にしたがって」と指示があれば、導関数の定義式をしっかりと書く必要があります。
まず、問題の関数を \(y = f(x)\) とおきます。
\(f(x) = x^2 − 3x + 9\) とする。
単純に関数を \(y\) のままで導関数を \(y’\) と表すこともできますが、導関数の定義から考えるときは \(y = f(x)\) とおいた方が考えやすくなります。
導関数はある点(瞬間)における変化率ですから、\(x\) をちょっと(\(h\))だけ動かしたときの \(y\) の変化の割合、その移動量 \(h\) を極限まで \(0\) に近づけるから…と考え、式を立てます。
\(\displaystyle f’(x) = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}\)
これが、導関数の定義式でしたね。
問題の関数を定義式に代入していきます。
先に分子の \(f(x + h) − f(x)\) を計算して整理しておくと後が楽です。
(見切れる場合は横へスクロール)
\(f(x + h) − f(x)\)
\(= \{(x + h)^2 − 3(x + h) + 9\} − (x^2 − 3x + 9)\)
\(= x^2 + 2hx + h^2 − 3x − 3h + 9 − x^2 + 3x − 9\)
\(= 2hx + h^2 − 3h\)
\(= h(2x + h − 3)\)
分子が求められたら、定義式全体に戻りましょう。
\(\begin{align} f’(x) &= \lim_{h \to 0} \frac{f(x + h) − f(x)}{h} \\ &= \lim_{h \to 0} \frac{h(2x + h − 3)}{h} \\ &= \lim_{h \to 0} (2x + h − 3) \end{align}\)
中身がこれ以上簡単にできなくなったら、極限 (\(\lim\)) を考えます。
中身の式 \(2x + h − 3\) において、\(h\) を限りなく \(0\) に近づける(つまり、\(0\) で近似する)と…
\(\begin{align} f’(x) &= \lim_{h \to 0} (2x + h − 3) \\ &= 2x − 3 \end{align}\)
これで、\(y = x^2 − 3x + 9\) の導関数は \(\color{red}{y’ = 2x − 3}\) と求められました!
「極限」の考え方がよくわからない場合は、以下の記事を確認しましょう。
 極限とは?公式一覧や極限計算のポイントをわかりやすく解説!
極限とは?公式一覧や極限計算のポイントをわかりやすく解説!
② 微分公式を使って求める
\(y = x^2 − 3x + 9\) の導関数を求めよ。
単に「微分せよ」「導関数を求めよ」と指示された場合は、微分公式を利用して楽に導関数を求めることができます。
この問題では、べき乗の微分公式 \((x^n)’ = nx^{n − 1}\) および定数の微分公式 \((k)’ = 0\) を利用します。
\(\begin{align}y’ &= (x^2 − 3x + 9)’ \\&= (x^2)’ − 3(x)’ + (9)’\\&= 2x − 3 \cdot 1 + 0 \\&= 2x − 3\end{align}\)
答え: \(\color{red}{y’ = 2x − 3}\)
高校で習うすべての微分公式を説明しています。
 微分とは?微分のやり方と全公式をわかりやすく解説!
微分とは?微分のやり方と全公式をわかりやすく解説!
微分係数の求め方
微分係数も、状況によって次の \(2\) 通りの求め方があります。

- 問題文に「微分係数の定義にしたがって」とある場合
→ ① 微分係数の定義から求める - 問題文に指示がない or 事前に導関数が求めてある場合
→ ② 導関数に代入して求める
それぞれの求め方を同じ例題で説明します。
① 微分係数の定義から求める
微分係数の定義にしたがって、次の関数の \(x = 1\) における微分係数を求めよ。
\(f(x) = x^2 − 3x + 9\)
「微分係数の定義にしたがって」とあるので、定義どおり計算していきます。
途中、代入計算があるので、問題の関数を \(y = f(x)\) とおいておきます。
\(f(x) = x^2 − 3x + 9\) とおく。
移動前の \(x\) を \(1\)、ちょっとの移動量を \(h\) として、微分係数の定義式を立てます。
関数 \(f(x)\) の \(x = 1\) における微分係数は
\(\displaystyle f’(1) = \lim_{h \to 0} \frac{f(1 + h) − f(1)}{h}\)
問題の関数を定義式に代入していきます。
先に分子の \(f(1 + h) − f(1)\) を計算して整理しておくと後が楽です。
\(f(1 + h) − f(1)\)
\(= (1 + h)^2 − 3(1 + h) + 9 − (1 − 3 + 9)\)
\(= 1 + 2h + h^2 − 3 − 3h + 9 − 7\)
\(= h^2 − h\)
\(= h(h − 1)\)
分子が求められたら、定義式に戻りましょう。
\(\begin{align} f’(1) &= \lim_{h \to 0} \frac{f(1 + h) − f(1)}{h} \\ &= \lim_{h \to 0} \frac{h(h − 1)}{h} \\ &= \lim_{h \to 0} (h − 1) \end{align}\)
中身がこれ以上簡単にできなくなったら、極限 (\(\lim\)) を考えます。
中身の部分 \((h − 1)\) において、 \(h\) を限りなく \(0\) に近づける(つまり、\(0\) で近似する)と…
\(\begin{align} f’(x) &= \lim_{h \to 0} (h − 1) \\ &= −1 \end{align}\)
これで、\(x = 1\) における微分係数は \(\color{red}{f’(1) = −1}\) と求められましたね!
② 導関数に代入して求める
次の関数の \(x = 1\) における微分係数を求めよ。
\(f(x) = x^2 − 3x + 9\)
問題文に「定義を使って」などの指示が特になかったり、前の小問ですでに導関数が求めてある場合には、導関数に \(x\) 座標を代入する方法で微分係数を求めることができます。
\(f(x) = x^2 − 3x + 9\) の導関数は、
\(f’(x) = 2x − 3\)
\(x = 1\) のときの微分係数は
\(f’(1) = 2 \cdot 1 − 3 = −1\)
答え: \(\color{red}{−1}\)
導関数・微分係数の計算問題
最後に、導関数や微分係数の計算問題に挑戦しましょう!
計算問題①「\(4x^2 + 1\) の導関数(定義から)」
次の関数を、導関数の定義にしたがって微分しなさい。
\(f(x) = 4x^2 + 1\)

「導関数の定義にしたがって」とあるときは、微分の計算公式ではなく、導関数の定義式できちんと微分を行うのでしたね。
\(\displaystyle f’(x) = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}\)
ここで、
\(f(x + h) − f(x)\)
\(= \{4(x + h)^2 + 1\} − (4x^2 + 1)\)
\(= 4(x^2 + 2hx + h^2) + 1 − 4x^2 − 1\)
\(= 4x^2 + 8hx + 4h^2 − 4x^2\)
\(= 8hx + 4h^2\)
\(= 4h(2x + h)\)
であるから、
\(\begin{align} f’(x) &= \lim_{h \to 0} \frac{4h(2x + h)}{h} \\ &= \lim_{h \to 0} 4(2x + h) \\ &= 4(2x + 0) \\ &= 8x \end{align}\)
答え: \(\color{red}{f’(x) = 8x}\)
計算問題②「\(−2x^2 + 5x + 3\) の微分係数(定義から)」
関数 \(f(x) = −2x^2 + 5x + 3\) について、微分係数の定義にしたがって、\(x = −1\) における微分係数を求めよ。

微分係数についても、「定義にしたがって」とあれば定義式どおりに計算します。
関数 \(f(x)\) の \(x = −1\) における微分係数は
\(\displaystyle f’(−1) = \lim_{h \to 0} \frac{f(−1 + h) − f(−1)}{h}\)
ここで、
\(\displaystyle f(−1 + h) − f(−1)\)
\(= \{−2(−1 + h)^2 + 5(−1 + h) + 3\} − (−2 − 5 + 3)\)
\(= \{−2(1 − 2h + h^2) − 5 + 5h + 3\} − (−4)\)
\(= −2 + 4h − 2h^2 − 5 + 5h + 3 + 4\)
\(= −2h^2 + 9h\)
\(= h(−2h + 9)\)
(見切れる場合は横へスクロール)
であるから、
\(\begin{align}\displaystyle f’(−1) &= \lim_{h \to 0} \frac{h(−2h + 9)}{h}\\&= \lim_{h \to 0} (−2h + 9)\\&= 9\end{align}\)
答え: \(\color{red}{f’(−1) = 9}\)
計算問題③「\(x^2 − 7x + 1\) の導関数と微分係数」
関数 \(f(x) = x^2 − 7x + 1\) について、以下の問いに答えよ。
(1) 導関数 \(f'(x)\) を求めよ。
(2) \(x = 3\) における微分係数を求めよ。

「定義にしたがって」という言葉がなければ、導関数は微分公式で求めて構いません。
微分係数は、求めた導関数に \(x\) の値を代入するだけで簡単に求められますね。
(1)
\(\begin{align} f’(x) &= (x^2 − 7x + 1)’ \\ &= (x^2)’ − 7(x)’ + (1)’ \\ &= 2x − 7 \end{align}\)
答え: \(\color{red}{f’(x) = 2x − 7}\)
(2)
\(x = 3\) における微分係数 \(f’(3)\) は
\(\begin{align} f’(3) &= 2 \cdot 3 − 7 \\ &= 6 − 7 \\ &= −1 \end{align}\)
答え: \(\color{red}{−1}\)
以上で計算問題も終わりです!
導関数と微分係数は急に出てきて覚えにくい言葉ですが、意味と定義をしっかりと理解しておけばなんてことはありません。
計算練習を積んで、理解を深めていきましょう!

理解には個人差がありますが 幾つものサイトを渡り ここへ来てやっと 微分を納得できた気分になっています
ありがとうごさいました
この度はコメントいただきありがとうございます。
当サイト記事がお役に立てておりましたら何よりです。
今後ともどうぞ当サイトをよろしくお願いいたします。