この記事では、「微分」とは何かをわかりやすく解説していきます。
微分のやり方や、高校で習う微分公式を例題付きで解説していきますので、この記事を通してぜひマスターしてくださいね。
目次
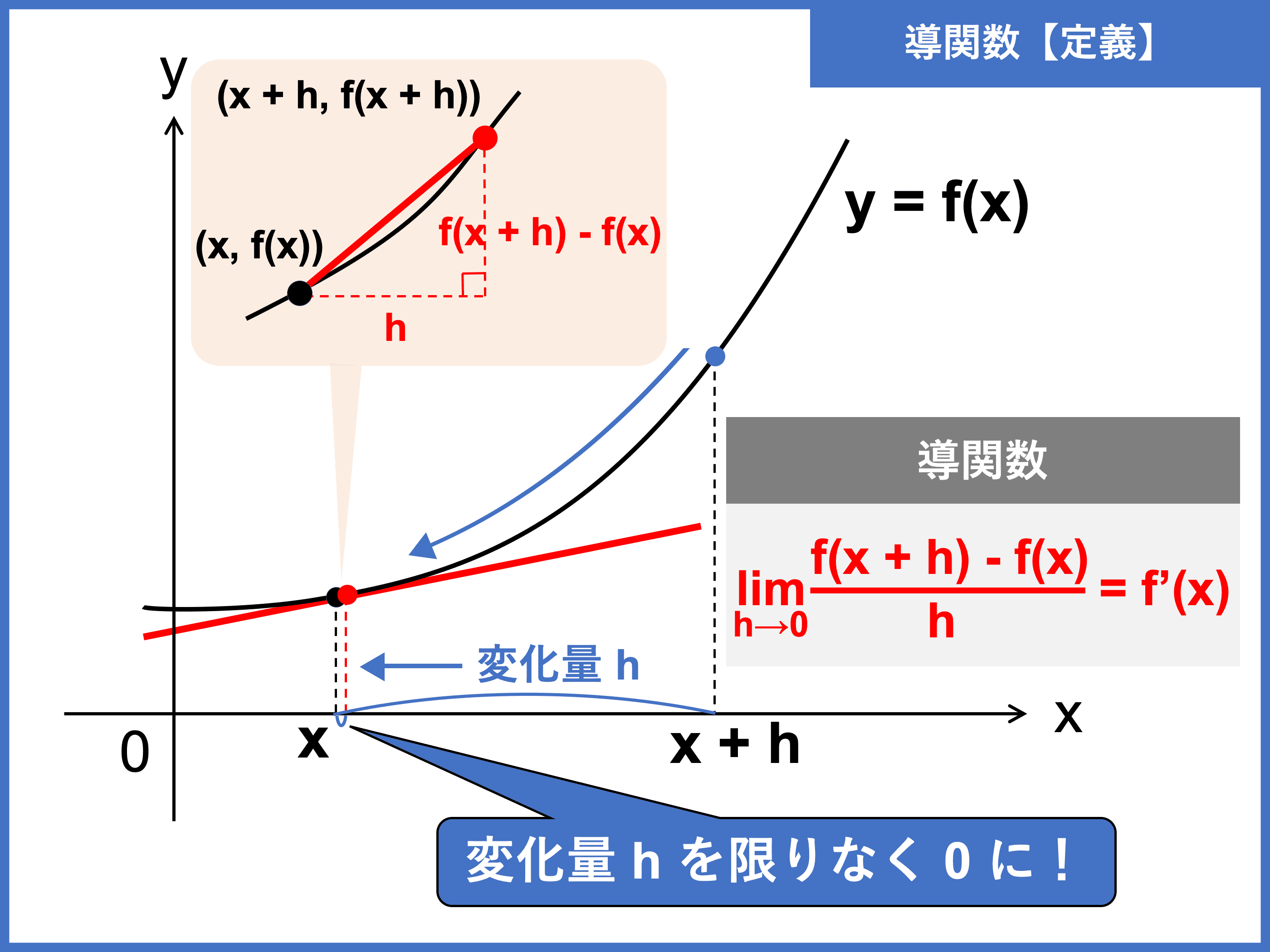
微分とは?
微分とは、ある関数 \(f(x)\) の導関数 \(f'(x)\) を求める演算のことです。
さて、では導関数って何?と思いますよね。
導関数とは、関数 \(y = f(x)\) のある点における瞬間の変化率(すなわち接線の傾き)を求められる関数で、次のように定義されます。
関数 \(f(x)\) の導関数 \(f'(x)\) は
\begin{align}\color{red}{\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}}\end{align}
微分の記号
微分することは、元の関数に「\(\bf{{}’}\)」をつけて表すことが多いです。
関数 \(y = f(x)\) を \(x\) について微分することを次のように表す。
\(\color{red}{f'(x)}\) または \(\color{red}{y’}\)
(例)
- \(y = x^2 + 2x + 3\) を微分
→ \((x^2 + 2x + 3)\color{salmon}{{}’}\) または \(y\color{salmon}{{}’}\) - \(y = 3x^3 + 1\) を微分
→ \((3x^3 + 1)\color{salmon}{{}’}\) または \(y\color{salmon}{{}’}\)
ただし、「\({}’\)」で表すと、関数を何で微分するのかがあいまいになってしまいます。
そこで、対象を明確にした次のような表記を使うこともあります。
関数 \(y = f(x)\) を \(x\) について微分することを次のように表す。
\(\color{red}{\displaystyle \frac{dy}{dx}}\) または \(\color{red}{\displaystyle \frac{d}{dx} f(x)}\)
分数のようなかたちで、「分子の関数を分母の変数で微分する」ことを表しています。
これで、何についての微分なのかが簡単に表現できます。
(例)
- \(y = g(x)\) を \(x\) について微分
→ \(\color{salmon}{\displaystyle \frac{dy}{dx}}\) または \(\color{salmon}{\displaystyle \frac{d}{dx} g(x)}\) - \(x = 2t^2 + t − 1\) を \(t\) について微分
→ \(\color{salmon}{\displaystyle \frac{dx}{dt}}\)
問題の中で微分する対象が明確な場合は「\({}’\)」による表記で大丈夫です!
微分のやり方
微分には、「① 導関数の定義に従ったやり方」と「② 微分公式を利用するやり方」があります。
① 導関数の定義に従って微分する
まずは導関数の定義に従った微分のやり方です。
次の関数を微分せよ。
\(y = x^2 − 3x + 9\)
導関数の定義式 \(\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}\) に問題の関数を当てはめて、導関数 \(y’\) を求めます。
\(y = f(x)\) とおくと、
\(\displaystyle y’ = \lim_{h \to 0} \frac{f(x + h) − f(x)}{h}\)
\(f(x + h) − f(x)\)
\(= \{(x + h)^2 − 3(x + h) + 9\} \) \(− \ (x^2 − 3x + 9)\)
\(= (x^2 + 2hx + h^2 − 3x − 3h + 9) \) \(− \ x^2 + 3x − 9\)
\(= 2hx + h^2 − 3h\)
\(= h(2x + h − 3)\)
よって、
\(\begin{align}\displaystyle y’ &= \lim_{h \to 0} \frac{h(2x + h − 3)}{h} \\&= \lim_{h \to 0} (2x + h − 3) \\&= 2x − 3\end{align}\)
答え: \(\color{red}{y’ = 2x − 3}\)
これが、導関数の定義に従った微分のやり方です。
しかし、関数を微分するたびに定義どおりの計算を行うのは大変ですよね。
そこで、次に示すやり方②のように微分の法則性をまとめた公式を使うことで、計算を省略することができます。
② 微分公式を使って微分する
次に、微分公式を使った微分のやり方です。
次の関数を微分せよ。
\(y = x^2 − 3x + 9\)
先ほどと同じ例題ですが、微分公式を使うと一瞬で答えにたどり着けます。
なお、この問題で使う微分公式はかっこ書きのリンクから確認できます。
以降、高校で習うすべての微分公式を、数IIで習う基本公式と数IIIで習う応用公式に分けて説明していきます。
微分の基本公式一覧(数II)
ここでは、主に数IIで習う基本的な微分公式を解説します。
以降、\(f(x)\), \(g(x)\) を \(x\) の関数とし、\(\alpha\), \(\beta\) を定数として公式を示していきます。
定数倍の微分
関数に定数倍の係数がかかっている場合は、係数を微分の外に出すことができます。
\begin{align}\color{red}{(\alpha \, f(x))’ = \alpha \, f’(x)}\end{align}
(例)
- \((3x)’ = 3(x)’\)
- \((−5x^2)’ = −5(x^2)’\)
- \(\displaystyle \left\{ \frac{1}{2} (x^3 + 5x − 1) \right\}’ \) \(= \displaystyle \frac{1}{2} (x^3 + 5x − 1)’\)
和と差の微分
複数の関数の和や差で表された式は、個々の関数に分けて微分できます。
- \(\color{red}{(f(x) + g(x))’ = f'(x) + g'(x)}\)
- \(\color{red}{(f(x) − g(x))’ = f'(x) − g'(x)}\)
- \(\color{red}{(\alpha \, f(x) + \beta \, g(x))’ = \alpha \, f'(x) + \beta \, g'(x)}\)
- \(\color{red}{(\alpha \, f(x) − \beta \, g(x))’ = \alpha \, f'(x) − \beta \, g'(x)}\)
つまり、多項式を微分する場合は項ごとに微分できるということですね。
(例)
- \((x^2 − 3x + 9)’ = (x^2)’ − 3(x)’ + (9)’\)
- \((2x^3 + 5x − 3)’ \) \(= 2(x^3)’ + 5(x)’ − (3)’\)
べき乗の微分
べき乗 \(x^n\) の関数は、次のように微分できます。
\(n\) が自然数のとき、
\(\color{red}{(x^n)’ = nx^{n − 1}}\)
※ なお、\(p\) が有理数であっても、
\(\color{red}{(x^p)’ = px^{p − 1}}\)
が成り立つ。
べき乗の項を微分するときは、指数を係数として前に下ろし、指数は \(1\) を引けばよいのですね。
(例)
- \((x)’ = (x^1)’ = 1 x^{0} = 1\)
- \((x^2)’ = 2x^1 = 2x\)
- \((x^\frac{4}{3})’ = \displaystyle \frac{4}{3} x^{\frac{4}{3} − 1} = \displaystyle \frac{4}{3}x^\frac{1}{3}\)
- \((x^{−4})’ = (−4) x^{−4 − 1} = −4x^{−5}\)
※ で示したように、指数が分数や負の数であっても公式は成り立ちます。
定数の微分
一方、定数項を微分すると必ず \(0\) となります。
\(k\) が実数のとき、
\(\color{red}{(k)’ = 0}\)
(例)
- \((9)’ = 0\)
- \((−16)’ = 0\)
以上が、微分の基本公式でした。
例題「基本公式を使って微分する」
次の関数を微分せよ。
(1) \(y = 4x^3 − 5x^2 − 3x − 6\)
(2) \(y = (5x + 3)(x − 2)\)
(3) \(y = x^{−3} + x^{\frac{1}{2}} + 1\)

因数分解されていれば、微分する前に展開しておきます。
微分するときは、個々の項に分けて考えます。べき乗の微分は慣れるまでていねいに計算しましょう。
(1)
\(\begin{align}y’ &= (4x^3 − 5x^2 − 3x − 6)’\\&= 4(x^3)’ − 5(x^2)’ − 3(x)’ − (6)’\\&= 4 \cdot 3x^2 − 5 \cdot 2x^1 − 3 \cdot 1x^0 − 0\\&= 12x^2 − 10x − 3\end{align}\)
答え: \(\color{red}{12x^2 − 10x − 3}\)
(2)
\((5x + 3)(x − 2) = 5x^2 − 7x − 6\) より、
\(\begin{align}y’ &= (5x^2 − 7x − 6)’\\&= 5(x^2)’ − 7(x)’ − (6)’\\&= 5 \cdot 2x − 7 \cdot 1 − 0\\&= 10x − 7\end{align}\)
答え: \(\color{red}{10x − 7}\)
(3)
\(\begin{align}y’ &= (x^{−3} + x^{\frac{1}{2}} + 1)’\\&= (x^{−3})’ + (x^{\frac{1}{2}})’ + (1)’\\&\displaystyle = −3x^{−4} + \frac{1}{2} x^{−\frac{1}{2}} + 0\\&\displaystyle= −3x^{−4} + \frac{1}{2} x^{−\frac{1}{2}}\\&\displaystyle \left(= −\frac{3}{x^4} + \frac{1}{2\sqrt{x}}\right)\end{align}\)
答え: \(\color{red}{\displaystyle −3x^{−4} + \frac{1}{2} x^{−\frac{1}{2}}}\) または \(\color{red}{−\displaystyle \frac{3}{x^4} + \frac{1}{2\sqrt{x}}}\)
数IIまで勉強する方は、ここまで理解できていれば大丈夫です!
微分の応用公式一覧(数III)
続いて、数IIIで習う微分の応用公式を紹介していきます。
これらの公式を使うと、より複雑な関数の微分が可能になります。
三角関数の微分
まずは三角関数の微分公式です。
- \(\color{red}{(\sin x)’ = \cos x}\)
- \(\color{red}{(\cos x)’ = −\sin x}\)
- \(\color{red}{\displaystyle (\tan x)’ = \frac{1}{\cos^2 x}}\)
\(\sin x\), \(\cos x\), \(\tan x\) の微分の \(3\) 点セットは必ず暗記しておきましょう!
例題「三角関数を微分する」
次の関数を微分せよ。
\(y = \sin x + \cos x − \tan x\)
\(\cos x\) の微分だけ符号が変わることに注意します。
\(\begin{align}y’ &= (\sin x)’ + (\cos x)’ − (\tan x)’\\&\displaystyle = \cos x − \sin x − \frac{1}{\cos^2 x}\end{align}\)
答え: \(\color{red}{\cos x − \sin x − \displaystyle \frac{1}{\cos^2 x}}\)
指数関数の微分
続いて、指数関数の微分公式です。
\(a > 0\), \(a \neq 1\) のとき、
- \(\color{red}{(e^x)’ = e^x}\)
- \(\color{red}{(a^x)’ = a^x \log a}\)
\(e^x\) は微分しても式が変わらないことを覚えておきましょう。
例題「指数関数を微分する」
次の関数を微分せよ。
(1) \(y = −2 e^x\)
(2) \(y = 3^x\)
(1) \(y’ = −2(e^x)’ = −2e^x\)
(2) \(y’ = (3^x)’ = 3^x \log 3\)
答え: (1) \(\color{red}{−2e^x}\)、(2) \(\color{red}{3^x \log 3}\)
対数関数の微分
対数関数の微分公式は次の通りです。
\(a > 0\), \(a \neq 1\) のとき、
- \(\color{red}{\displaystyle (\log x)’ = \frac{1}{x}}\)
- \(\color{red}{\displaystyle (\log_a x)’ = \frac{1}{x \log a}}\)
- \(\color{red}{\displaystyle (\log |x|)’ = \frac{1}{x}}\)
- \(\color{red}{\displaystyle(\log_a |x|)’ = \frac{1}{x \log a}}\)
特に \((\displaystyle \log x)’ = \frac{1}{x}\) はよく使うので必ず覚えておきましょう!
底が \(e\) の自然対数「\(\log_e x\)」は、 \(e\) を省略して「\(\log x\)」と書くことが多いです。
例題「対数関数を微分する」
次の関数を微分せよ。
(1) \(y = 3 \log |x|\)
(2) \(y = 2 \log_5 x\)
(1) \(y’ = 3(\log|x|)’ = \displaystyle \frac{3}{x}\)
(2) \(y’ = 2(\log_5 x)’ = \displaystyle \frac{2}{x \log 5}\)
答え: (1) \(\color{red}{\displaystyle \frac{3}{x}}\)、(2) \(\color{red}{\displaystyle \frac{2}{x \log 5}}\)
積の微分
\(2\) つの関数のかけ算で表された関数は、交互に微分して足し合わせてあげます。
\begin{align}\color{red}{(f(x)g(x))’ = f’(x)g(x) + f(x)g’(x)}\end{align}
例題「べき乗関数と対数関数の積を微分する」
\(y = x^3 \log x\) を微分せよ。
関数 \(x^3\) と関数 \(\log x\) がかけ算された積の微分ですね。
\(\begin{align}y’ &= (x^3)’ \log x + x^3 (\log x)’\\&\displaystyle = 3x^2 \log x + x^3 \cdot \frac{1}{x}\\&= 3x^2 \log x + x^2\\&= x^2(3 \log x + 1)\end{align}\)
答え: \(\color{red}{x^2(3 \log x + 1)}\)
商の微分
関数同士の割り算で表された関数は、分母を \(2\) 乗し、分子に「\(\displaystyle (\text{分子の微分})(\text{分母}) − (\text{分子})(\text{分母の微分})\)」をもってきます。
\begin{align}\color{red}{\displaystyle \left( \frac{f(x)}{g(x)} \right)’ = \frac{f’(x)g(x) − f(x)g’(x)}{\{g(x)\}^2}}\end{align}
特に \(f(x) = 1\) のとき
\begin{align}\color{red}{\displaystyle \left( \frac{1}{g(x)} \right)’ = −\frac{g’(x)}{\{g(x)\}^2}}\end{align}
少し覚えづらいですが、問題をたくさん解いて頭に叩き込みましょう。
例題「分数関数を微分する」
\(\displaystyle y = \frac{x^2 + x − 1}{x^2 + 1}\) を微分せよ。
関数が関数で割られているので、商の微分が使えますね。
(見切れる場合は横へスクロール)
\(\displaystyle y’\)
\(\displaystyle = \frac{(x^2 + x − 1)’(x^2 + 1) − (x^2 + x − 1)(x^2 + 1)’}{(x^2 + 1)^2}\)
\(\displaystyle = \frac{(2x + 1)(x^2 + 1) − (x^2 + x − 1)2x}{(x^2 + 1)^2}\)
\(\displaystyle = \frac{(2x^3 + 2x + x^2 + 1) − (2x^3 + 2x^2 − 2x)}{(x^2 + 1)^2}\)
\(\displaystyle = \frac{−x^2 + 4x + 1}{(x^2 + 1)^2}\)
\(\displaystyle = −\frac{x^2 − 4x − 1}{(x^2 + 1)^2}\)
答え: \(\displaystyle \color{red}{−\frac{x^2 − 4x − 1}{(x^2 + 1)^2}}\)
合成関数の微分
続いて、\(2\) つの関数が合成された関数の微分方法です。
\(y\) が \(u\) の関数で、\(u\) が \(x\) の関数であるとき、\(y\) を \(x\) について微分すると
\begin{align}\color{red}{\displaystyle \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}}\end{align}
\(y = f(u)\), \(u = g(x)\) とおくと
\begin{align}\color{red}{y’ = \{f(g(x))\}’ = f’(g(x)) g’(x)}\end{align}
\(u = g(x)\) を箱とみて、「\((\text{全体を箱について微分}) \times (\text{箱の中身を微分})\)」をすると覚えておきましょう。
例題①「因数分解された関数を微分する」
\(y = (x^2 − 2)^3\) を微分せよ。
このまま解こうと思うと、右辺を展開する必要があります。
ここで、括弧の中身 \(x^2 − 2\) を \(1\) つの箱 \(□\) と見ると、
- \(y = □^3\)
- \(□ = x^2 − 2\)
という \(2\) つの関数が合成されていると見ることができます。
この合成関数を \(x\) について微分すると、
\(y’ = (□^3)’ □’\)
と計算できます。
実際にやってみましょう。
\(y = (x^2 − 2)^3\) を微分すると、
\(\begin{align} y’ &= 3(x^2 − 2)^2 \cdot (x^2 − 2)’ \\&= 3(x^2 − 2)^2 \cdot 2x \\ &= 6x(x^2 − 2)^2 \end{align}\)
答え: \(\color{red}{6x(x^2 − 2)^2}\)
全体を \(□\) について微分するときは、\(□\) を単なる変数と見ることがポイントです。
もう \(1\) 問、合成関数の問題を見てみましょう。
例題②「3 つの関数が合成された関数を微分する」
\(y = \log(\sin^2 x)\)
今度は、対数関数 \(\log □\) と三角関数 \(□ = \sin^2 x\) が合成されていますね。
また、\(\sin^2 x\) も \(□ = △^2\) と \(△ = \sin x\) が合成されているので、二重に合成されていることになります。
\(y’ = (\log □)’□’ = (\log □)’ 2△ △’\)
それでは解答です。
\(y = \log(\sin^2 x)\)
\(\begin{align} y’ &= \frac{1}{\sin^2 x} \cdot 2 \sin x \cdot \cos x \\ &= \frac{2 \cos x}{\sin x}\end{align}\)
答え: \(\color{red}{\displaystyle \frac{2 \cos x}{\sin x}}\)
いかがでしたか?
合成関数の微分は間違えやすいので、たくさん練習を積んでコツをつかんでいきましょう。
対数微分法
対数微分法とは、両辺の対数をとってから微分する方法で、累乗の積や商で表された関数を微分するときに便利です。
\(y = f(x)\) を対数微分法で微分する手順は次のとおりである。
- \(y = f(x)\) の両辺の絶対値の自然対数をとる(ただし、\(y = f(x) \neq 0\) )
\(\log |y| = \log |f(x)|\)
- 両辺を \(x\) で微分する
合成関数の微分の考え方から
\(\displaystyle \left( \frac{d}{dy} \log |y| \right) \frac{dy}{dx} \) \(= \displaystyle \left( \frac{d}{df(x)} \log |f(x)| \right) \frac{d}{dx} f(x)\)
よって、\(\displaystyle \frac{1}{y} \frac{dy}{dx} = \frac{1}{f(x)} f’(x)\)
- 左辺が \(\displaystyle \frac{dy}{dx}\) (求めたい導関数)だけになるように式変形する
両辺に \(y\) をかけて
\(\displaystyle \frac{dy}{dx} = \frac{y}{f(x)} f’(x)\)
\(y = f(x)\) より \(\displaystyle \frac{y}{f(x)} = 1\) であるから、
\(\displaystyle \frac{dy}{dx} = f’(x)\)
最初に両辺の絶対値の自然対数をとるのは、真数条件(真数 \(> 0\))を満たすためです。
あらかじめ両辺が正の数とわかっている場合は、絶対値は必要ありません。
また、とるのは必ず底が \(e\) の「自然対数」です。
 真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
対数微分法が力を発揮する問題例を \(2\) つ示します。
例題①「指数が三角関数のべき乗関数を微分する」
\(x > 0\) のとき、\(y = x^{\sin x}\) を微分せよ。
指数部分が \(x\) の三角関数になっているため、通常のべき乗の微分では解くことができません。
このようなときに、対数微分法を活用します。
\(x > 0\) より、\(y = x^{\sin x} > 0\)
両辺の自然対数をとって、
\(\log y = \log x^{\sin x}\)
\(\log y = \sin x \log x\)
両辺を \(x\) で微分して
\(\displaystyle \frac{y’}{y} = (\sin x)’ \log x + \sin x (\log x)’\)
\(\displaystyle \frac{y’}{y} = \cos x \log x + \frac{\sin x}{x}\)
\(y \neq 0\) より、両辺に \(y\) をかけて、
\(\begin{align} y’ &= \left( \cos x \log x + \frac{\sin x}{x} \right) y \\ &= \left( \cos x \log x + \frac{\sin x}{x} \right) x^{\sin x} \end{align}\)
答え: \(\color{red}{\displaystyle y’ = \left( \cos x \log x + \frac{\sin x}{x} \right) x^{\sin x}}\)
もう \(1\) 問見てみましょう。
例題②「複雑な積や累乗からなる関数を微分する」
\(y = \sqrt[3]{x^2 (x + 1)}\) を微分せよ。
複雑な積や累乗で表された式ですね。
指数に直して微分することもできますが、対数微分法で解いた方が圧倒的に楽です。
両辺の絶対値の自然対数をとって、
\(\log |y| = \log |x^2(x + 1)|^{\frac{1}{3}}\)
\(\displaystyle \log |y| = \frac{1}{3} (2 \log |x| + \log |x + 1|)\)
両辺を \(x\) で微分して、
\(\begin{align}\displaystyle \frac{y’}{y} &= \frac{1}{3} \left\{ \frac{2x’}{x} + \frac{(x + 1)’}{x + 1} \right\}\\&\displaystyle = \frac{1}{3} \left( \frac{2}{x} + \frac{1}{x + 1} \right)\\&\displaystyle = \frac{2(x + 1) + x}{3x(x + 1)}\\&\displaystyle = \frac{3x + 2}{3x(x + 1)}\end{align}\)
両辺に \(y\) をかけて
\(\begin{align}y’ &= \frac{3x + 2}{3x(x + 1)} \cdot y \\&= \frac{3x + 2}{3x(x + 1)} \cdot \sqrt[3]{x^2(x + 1)} \\&= \frac{3x + 2}{3} \cdot \sqrt[3]{\frac{x^2(x + 1)}{x^3(x + 1)^3}} \\&= \frac{3x + 2}{3} \cdot \sqrt[3]{\frac{1}{x(x + 1)^2}}\end{align}\)
答え: \(\color{red}{\displaystyle y’ = \frac{3x + 2}{3} \cdot \sqrt[3]{\frac{1}{x(x + 1)^2}}}\)
微分公式は以上です!
微分は入試でも頻出の単元なので、苦手なままだとかなり痛いです。
とにかくたくさん問題を解いて、公式ややり方をマスターしていきましょう!
ここまでに紹介した微分公式は、すべて導関数の定義に基づいて証明できます。
個々の証明は以下の記事で解説しているので、気になる方はぜひ参考にしてみてくださいね!
 微分公式の証明一覧!導関数の定義どおりの導出を解説
微分公式の証明一覧!導関数の定義どおりの導出を解説






