この記事では、「対数関数」とは何かをわかりやすく解説していきます。
対数関数のグラフや対数方程式・対数不等式などの計算問題、微分積分の公式なども説明していきますので、ぜひこの記事を通してマスターしてくださいね。
目次
対数関数とは?
対数関数とは、対数の真数部分に変数を含む関数のことです。
\(a > 0\), \(a \neq 1\) のとき、\(a\) を底とする \(x\) の対数関数は
\begin{align}\color{red}{y = \log_a x}\end{align}
対数関数 \(y = \log_a x\) を定義するとき、底 \(a\) と真数 \(x\) には満たすべき条件があります。
- 底の条件 \(a > 0, a \neq 1\)
- 真数条件 \(x > 0\)
 真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
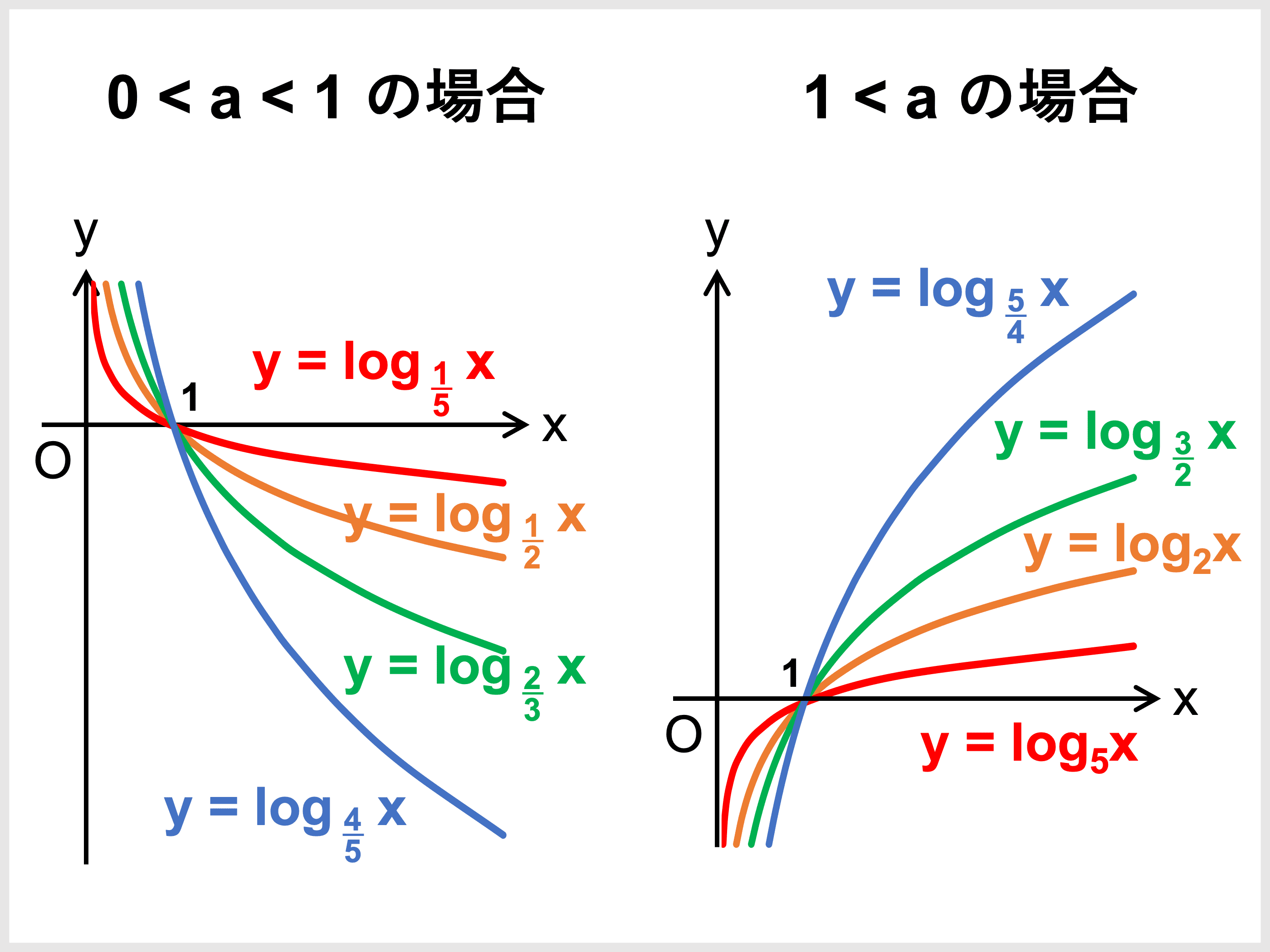
対数関数のグラフ
対数関数 \(y = \log_a x\) のグラフは次のようになります。

底 \(1 < a\) のときは右上がりの曲線、底 \(0 < a < 1\) のときは右下がりの曲線です。
また、対数関数の傾きは底の大きさによって次のように変化します。
対数関数の性質
対数関数には、次のような性質があります。
- 指数関数 \(y = a^x\) のグラフと直線 \(y = x\) に関して対称
- 定義域は正の数全体 \((x > 0)\)、値域は実数全体
- グラフは必ず点 \((1, 0), (a, 1)\) を通る
- \(y\) 軸を漸近線とする
- 底 \(a\) の範囲によって、グラフの増加傾向が異なる
-
- \(1 < a\) のとき
単調増加関数となる(\(x\) の値が増加すれば \(y\) の値も増加)
\begin{align}\color{red}{0 < p < q \iff \log_a p < \log_a q}\end{align} - \(0 < a < 1\) のとき
単調減少関数となる(\(x\) の値が増加すれば \(y\) の値は減少)
\begin{align}\color{red}{0 < p < q \iff \log_a p > \log_a q}\end{align}
(なお、\(a > 0\), \(a \neq 1\), \(p > 0\), \(q > 0\) で「\(p = q \iff \log_a p = \log_a q\)」が成り立つ)
- \(1 < a\) のとき

対数関数 \(y = \log_a x\) は、指数関数 \(y = a^x\) と逆関数の関係にあります。
対数関数の細かい特徴を忘れてしまったときは、指数関数と \(y = x\) に関して対称であることをとっかかりに思い出しましょう。
対数関数の計算公式
対数関数や対数を含む方程式・不等式の問題を解くには、「指数と対数の関係」「対数の性質」「底の変換公式」を理解しておきましょう。
\(a > 0, a \neq 1, M > 0\) のとき、
\begin{align}\color{red}{p = \log_a M \iff M = a^p}\end{align}
\(a > 0\), \(a \neq 1\), \(M > 0\), \(N > 0\) で、\(k\) は実数、\(n\) は \(2\) 以上の自然数のとき、
- \(\log_a a^k = k\)
特に、\(\log_a a = 1\), \(\log_a 1 = 0\), \(\displaystyle \log_a \frac{1}{a} = −1\) - \(\log_a MN = \log_a M + \log_a N\)
- \(\displaystyle \log_a \frac{M}{N} = \log_a M − \log_a N\)
- \(\log_a M^k = k \log_a M\)
- \(\displaystyle \log_a \sqrt[n]{M} = \frac{1}{n} \log_a M\)
\(a, b, c\) は正の数で \(a \neq 1\), \(b \neq 1\), \(c \neq 1\) のとき、
\begin{align}\displaystyle \log_a b = \frac{\log_c b}{\log_c a}\end{align}
特に、\(\displaystyle \log_a b = \frac{1}{\log_b a}\)
対数方程式の解き方【例題】
以下の例題を通して、対数方程式(対数関数を含む方程式)の解き方を説明します。
次の方程式を解け。
\(\log_2 (x + 2) = \log_4 (5x + 16)\)
対数を含む方程式では、まず真数条件または底の条件を確認します。
例題は真数に変数を含むので、真数条件を確認しましょう。
真数は正であるから、
\(x + 2 > 0\) かつ \(5x + 16 > 0\)
すなわち \(x > −2\) …①
式の中の対数の底をそろえたり、対数を合体・分解したりして、式を整理します。
例題では底が異なるので、底の変換公式で底をそろえましょう。
\(\begin{align} \log_4 (5x + 16) &= \frac{\log_2 (5x + 16)}{\log_2 4} \\ &= \frac{1}{2} \log_2 (5x + 16) \end{align}\)
より、
\(\displaystyle \log_2 (x + 2) = \frac{1}{2} \log_2 (5x + 16)\)
\(2\log_2 (x + 2) = \log_2 (5x + 16)\)
\(\log_a p = \log_a q\) の形が得られたら、次の性質を利用できます。
\(a > 0\), \(a \neq 1\), \(p > 0\), \(q > 0\) のとき、
\begin{align}\color{red}{\log_a p = \log_a q \iff p = q}\end{align}
これにより、真数に関する方程式が得られます。
\(\log_2 (x + 2)^2 = \log_2 (5x + 16)\) より
\((x + 2)^2 = 5x + 16\)
得られた方程式を解きます。
最初に調べた真数条件と照らし合わせて、\(x\) を求めましょう。
\((x + 2)^2 = 5x + 16\)
\(x^2 + 4x + 4 − 5x − 16 = 0\)
\(x^2 − x − 12 = 0\)
\((x + 3)(x − 4) = 0\)
①より、\(x = 4\)
答え: \(\color{red}{x = 4}\)
真数は正であるから、
\(x + 2 > 0\) かつ \(5x + 16 > 0\)
すなわち \(x > −2\) …①
\(\begin{align} \log_4 (5x + 16) &= \frac{\log_2 (5x + 16)}{\log_2 4} \\ &= \frac{1}{2} \log_2 (5x + 16) \end{align}\)
より、
\(\displaystyle \log_2 (x + 2) = \frac{1}{2} \log_2 (5x + 16)\)
\(2\log_2 (x + 2) = \log_2 (5x + 16)\)
よって
\((x + 2)^2 = 5x + 16\)
\(x^2 + 4x + 4 − 5x − 16 = 0\)
\(x^2 − x − 12 = 0\)
\((x + 3)(x − 4) = 0\)
①より、\(x = 4\)
答え: \(\color{red}{x = 4}\)
対数不等式の解き方【例題】
以下の例題を通して、対数不等式(対数関数を含む不等式)の解き方を説明します。
不等式 \(\log_2 (x − 2) < 1 + \log_{\frac{1}{2}} (x − 4)\) を解け。
対数不等式を解くときも、流れは対数方程式とほとんど同じです。最後に真数部分の大小関係を考えます。
真数部分に変数を含む場合は真数条件を、底に変数を含む場合は底の条件を確認します。
真数は正であるから、
\(x − 2 > 0\) かつ \(x − 4 > 0\)
すなわち \(x > 4\) …①
式の中の対数の底をそろえたり、対数を合体・分解したりして、式を整理します。
例題では、すべての項を底が \(2\) の対数にそろえてみましょう。
\(1 = \log_2 2\)、
\(\begin{align} \log_{\frac{1}{2}} (x − 4) &= \frac{\log_2 (x − 4)}{\log_2 \frac{1}{2}} \\ &= \frac{\log_2 (x − 4)}{\log_2 2^{−1}} \\ &= −\log_2 (x − 4) \end{align}\)
であるから、
\(\log_2 (x − 2) < 1 + \log_{\frac{1}{2}} (x − 4)\) は
\(\log_2 (x − 2) < \log_2 2 − \log_2 (x − 4)\)
と変形できる。
よって
\(\log_2 (x − 2) + \log_2 (x − 4) < \log_2 2\)
\(\log_2 (x − 2)(x − 4) < \log_2 2\)
式を整理できたら、対数関数の以下の性質を利用して真数に関する不等式を得ます。
- \(a > 1\) のとき
\begin{align}\color{red}{\log_a A < \log_a B \iff 0 < A < B}\end{align} - \(0 < a < 1\) のとき
\begin{align}\color{red}{\log_a A < \log_a B \iff A > B > 0}\end{align}
\(a > 1\) のときは不等式と真数部分の大小関係が一致しますが、\(0 < a < 1\) のときは大小関係が入れ替わることに注意しましょう。
\(\log_2 (x − 2)(x − 4) < \log_2 2\) において
底 \(2\) は \(1\) よりも大きいから、
\((x − 2)(x − 4) < 2\)
\(x^2 − 6x + 8 < 2\)
\(x^2 − 6x + 6 < 0\)
あとは、不等式を満たす \(x\) の値の範囲を求めます。
最初に調べた真数条件との共通範囲を求めることを忘れないでくださいね。
ここで、\(x^2 − 6x + 6 = 0\) を解くと
\(\begin{align} x &= 3 \pm \sqrt{3^2 − 1 \cdot 6} \\ &= 3 \pm \sqrt{3} \end{align}\)
であるから、
\(x^2 − 6x + 6 < 0\) を満たす \(x\) の値の範囲は
\(3 − \sqrt{3} < x < 3 + \sqrt{3}\)
①との共通範囲を求めて、
\(4 < x < 3 + \sqrt{3}\)
答え: \(\color{red}{4 < x < 3 + \sqrt{3}}\)
真数は正であるから、
\(x − 2 > 0\) かつ \(x − 4 > 0\)
すなわち \(x > 4\) …①
\(1 = \log_2 2\)、
\(\begin{align} \log_{\frac{1}{2}} (x − 4) &= \frac{\log_2 (x − 4)}{\log_2 \frac{1}{2}} \\ &= \frac{\log_2 (x − 4)}{\log_2 2^{−1}} \\ &= −\log_2 (x − 4) \end{align}\)
であるから、
\(\log_2 (x − 2) < 1 + \log_{\frac{1}{2}} (x − 4)\) は
\(\log_2 (x − 2) < \log_2 2 − \log_2 (x − 4)\)
と変形できる。
よって
\(\log_2 (x − 2) + \log_2 (x − 4) < \log_2 2\)
\(\log_2 (x − 2)(x − 4) < \log_2 2\)
\(\log_2 (x − 2)(x − 4) < \log_2 2\) において
底 \(2\) は \(1\) よりも大きいから、
\((x − 2)(x − 4) < 2\)
\(x^2 − 6x + 8 < 2\)
\(x^2 − 6x + 6 < 0\)
ここで、\(x^2 − 6x + 6 = 0\) を解くと
\(\begin{align} x &= 3 \pm \sqrt{3^2 − 1 \cdot 6} \\ &= 3 \pm \sqrt{3} \end{align}\)
であるから、
\(x^2 − 6x + 6 < 0\) を満たす \(x\) の値の範囲は
\(3 − \sqrt{3} < x < 3 + \sqrt{3}\)
①との共通範囲を求めて、
\(4 < x < 3 + \sqrt{3}\)
答え: \(\color{red}{4 < x < 3 + \sqrt{3}}\)
対数関数の計算問題
対数関数のグラフや性質に関する知識を使う計算問題に挑戦しましょう。
計算問題①「対数関数の平行移動とグラフ」
\(y = \log_8 (x + 2)^3 − 1\) のグラフは、\(y = \log_2 x\) のグラフを \(x\) 軸方向,\(y\) 軸方向にどれだけ平行移動したグラフであるか。
また、グラフの概形を書け。

グラフの平行移動の考え方は、対数関数であっても同じです。
グラフの平行移動
\(y = f(x)\) を \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\) だけ平行移動した関数は
\begin{align}y − q = f(x − p)\end{align}
\(\begin{align} y &= \log_8 (x + 2)^3 − 1 \\ &= \frac{\log_2 (x + 2)^3}{\log_2 8} − 1 \\ &= \frac{\log_2 (x + 2)^3}{\log_2 2^3} − 1 \\ &= \frac{3\log_2 (x + 2)}{3} − 1 \\ &= \log_2 (x + 2) − 1 \end{align}\)
より、
\(y = \log_2 x\) のグラフを \(x\) 軸方向に \(−2\)、\(y\) 軸方向に \(−1\) だけ平行移動したグラフである。
答え:
\(\color{red}{y = \log_2 x}\) のグラフを \(\color{red}{x}\) 軸方向に \(\color{red}{−2}\)、\(\color{red}{y}\) 軸方向に \(\color{red}{−1}\) だけ平行移動したグラフ
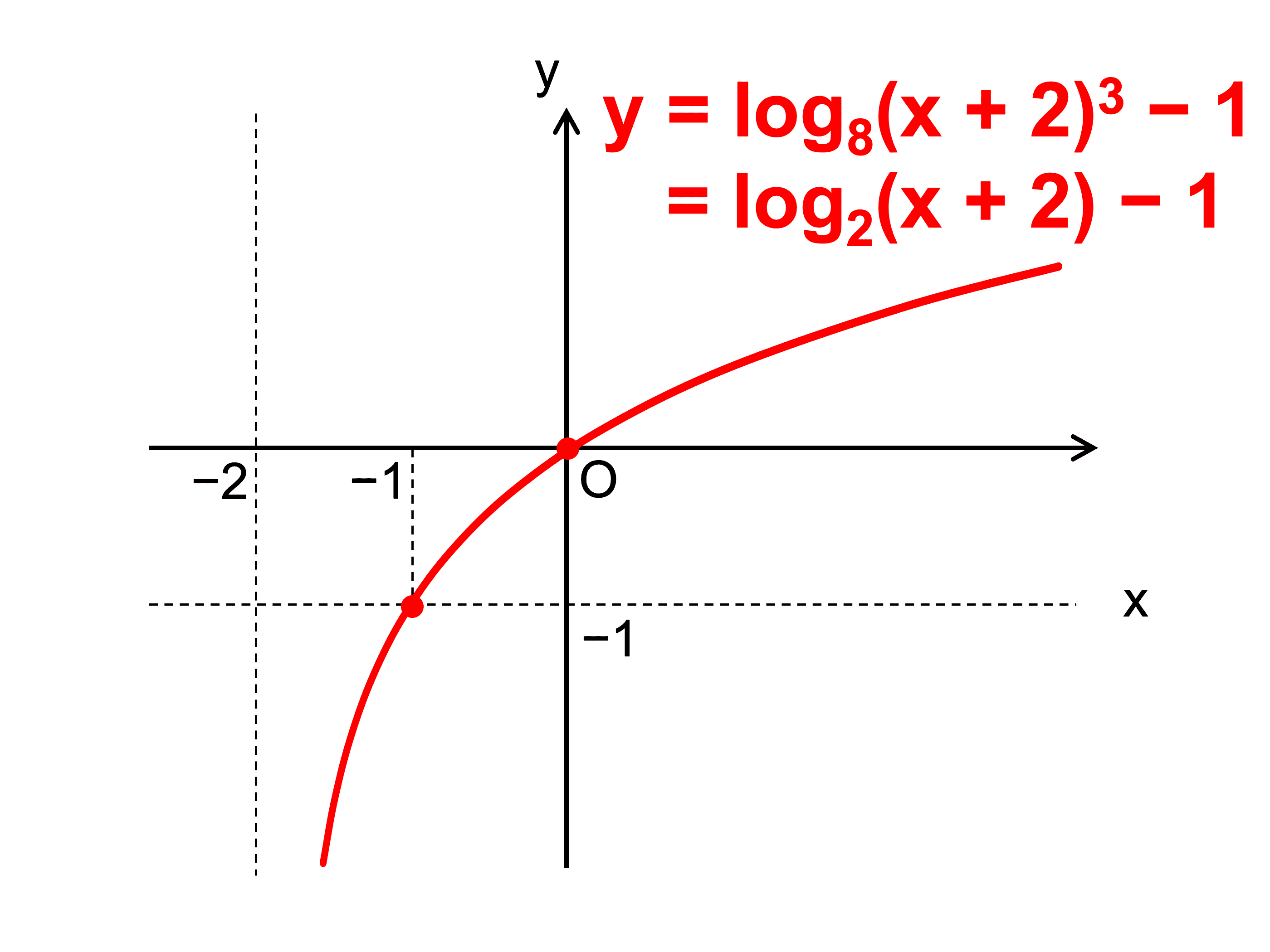
計算問題②「対数関数の最大値・最小値」
\(1 \leq x \leq 8\) のとき、関数 \(y = (\log_2 x)^2 + 4\log_{\frac{1}{4}} 2x + \log_2 32\) の最大値と最小値を求めよ。

右辺を整理して \(\log_2 x = t\) と変数を置き換えると、二次関数の最大・最小問題に落とし込めます。
置き換えた変数の定義域を調べること、最後は \(x\) について解くことを忘れないようにしましょう。
\(\log_2 x = t\) とおくと、\(1 \leq x \leq 8\) であるから
\(\log_2 1 \leq t \leq \log_2 8\)
すなわち
\(0 \leq t \leq 3\) …①
ここで、
\(\begin{align} \log_{\frac{1}{4}} 2x &= \frac{\log_2 2x}{\log_2 \frac{1}{4}} \\ &= \frac{\log_2 2x}{\log_2 2^{−2}} \\ &= \frac{\log_2 2 + \log_2 x}{−2} \\ &= −\frac{1}{2} (1 + t) \end{align}\)
\(\log_2 32 = \log_2 2^5 = 5\)
より、
\(y\) を \(t\) の式で表すと、
\(\begin{align} y &= (\log_2 x)^2 + 4\log_{\frac{1}{4}} 2x + \log_2 32 \\ &= t^2 + 4 \cdot \left( −\frac{1}{2} \right) (1 + t) + 5 \\ &= t^2 − 2 − 2t + 5 \\ &= t^2 − 2t + 3 \\ &= (t − 1)^2 + 2 \end{align}\)

①の範囲において、\(y\) は \(t = 3\) で最大値 \(6\)、\(t = 1\) で最小値 \(2\) をとる。
\(t = \log_2 x\) より \(x = 2^t\) であるから、
\(t = 3\) のとき \(x = 2^3 = 8\)
\(t = 1\) のとき \(x = 2^1 = 2\)
したがって、\(y\) は
\(x = 8\) のとき最大値 \(6\)、\(x = 2\) のとき最小値 \(2\) をとる。
答え:
\(\color{red}{x = 8}\) のとき最大値 \(\color{red}{6}\)、\(\color{red}{x = 2}\) のとき最小値 \(\color{red}{2}\)
計算問題③「底に変数を含む対数方程式」
次の方程式を解け。
\(\log_2x + 6\log_x 2 = 5\)

底と真数が逆の関係にある \(2\) つの対数がありますね。
このようなときは、底の変換公式から、以下が成り立つことを利用できます。
正の数 \(a, b\)(ただし \(a \neq 1\), \(b \neq 1\))のとき、
底の変換公式 \(\displaystyle \log_a b = \frac{1}{\log_b a}\) より
\begin{align}\color{red}{\log_a b \cdot \log_b a = 1}\end{align}
真数は正、底は \(1\) でない正の数であるから、
\(0 < x < 1\), \(1 < x\) …①
\(\log_2 x \neq 0\) より、両辺に \(\log_2 x\) をかけて
\((\log_2 x)^2 + 6\log_x 2 \cdot \log_2 x = 5\log_2 x\)
\((\log_2 x)^2 − 5\log_2 x + 6 = 0\)
\((\log_2 x − 2)(\log_2 x − 3) = 0\)
よって \(\log_2 x = 2, 3\)
\(\log_2 x = 2\) より \(x = 4\)
\(\log_2 x = 3\) より \(x = 8\)
これらは①を満たす。
したがって、\(x = 4, 8\)
答え: \(\color{red}{x = 4, 8}\)
対数関数の微分公式
対数関数の微分公式は次のとおりです。
\(a > 0\), \(a \neq 1\) のとき、
- \(\color{red}{\displaystyle (\log x)’ = \frac{1}{x}}\)
- \(\color{red}{\displaystyle (\log_a x)’ = \frac{1}{x \log a}}\)
- \(\color{red}{\displaystyle (\log |x|)’ = \frac{1}{x}}\)
- \(\color{red}{\displaystyle (\log_a |x|)’ = \frac{1}{x \log a}}\)
例題「対数関数を微分する」
次の例題を通して、対数関数の微分のやり方を説明します。
次の関数を微分せよ。
(1) \(y = \log_3 x\)
(2) \(y = \log_2 |2x|\)
(1) は公式に当てはめるだけですね。
(2) は、\(y = \log_2 |u|\) と \(u = 2x\) の合成関数なので、合成関数の微分が必要です(数III)。
(1)
\(\displaystyle y’ = \color{red}{\frac{1}{x \log 3}}\)
(2)
\(\begin{align} y’ &= \frac{(2x)’}{2x \log 2} \\ &= \frac{2}{2x \log 2} \\ &= \color{red}{\frac{1}{x \log 2}} \end{align}\)
対数関数の積分公式
対数関数の積分公式は次のとおりです。
積分定数を \(C\) とおくと、
\begin{align}\color{red}{\displaystyle \int \log x \, dx = x \log x − x + C}\end{align}
なお、対数関数は部分積分法で積分できるので、必ずしも公式を丸暗記する必要はありません(数III)。
\(\displaystyle \int \log x \, dx\)
\(\displaystyle = \int (x)’ \log x \, dx\)
\(\displaystyle = x \log x − \int x (\log x)’ \, dx\)
\(\displaystyle = x \log x − \int x \cdot \frac{1}{x} \, dx\)
\(\displaystyle = x \log x − \int 1 \, dx\)
\(= \color{red}{x \log x − x + C}\)(\(C\) は積分定数)
例題「対数関数を積分する」
次の例題を通して、対数関数の積分のやり方を説明します。
次の不定積分を求めよ。
(1) \(\displaystyle \int \log (x + 1) \ dx\)
(2) \(\displaystyle \int x^2 \log x \ dx\)
対数関数と別の関数の積の形をした関数は、部分積分法で計算します(数III)。
(1) でも、\(1 \cdot \log (x + 1)\) と見れば部分積分法を適用できます。
(1)
\(\displaystyle \int \log (x + 1) \, dx\)
\(\displaystyle = \int 1 \cdot \log (x + 1) \, dx\)
\(\displaystyle = \int (x + 1)’ \log (x + 1) \, dx\)
\(\displaystyle = (x + 1) \log (x + 1) − \int (x + 1) \{\log (x + 1)\}’ \, dx\)
\(\displaystyle = (x + 1) \log (x + 1) − \int (x + 1) \cdot \frac{1}{x + 1} \, dx\)
\(\displaystyle = (x + 1) \log (x + 1) − \int 1 \, dx\)
\(= \color{red}{(x + 1) \log (x + 1) − x + C}\)(\(C\) は積分定数)
(2)
\(\displaystyle \int x^2 \log x \, dx\)
\(\displaystyle = \int \left(\frac{x^3}{3}\right)’ \log x \, dx\)
\(\displaystyle = \frac{x^3}{3} \log x − \int \frac{x^3}{3} (\log x)’ \, dx\)
\(\displaystyle = \frac{x^3}{3} \log x − \int \frac{x^3}{3} \cdot \frac{1}{x} \, dx\)
\(\displaystyle = \frac{x^3}{3} \log x − \int \frac{x^2}{3} \, dx\)
\(= \color{red}{\displaystyle \frac{x^3}{3} \log x − \frac{x^3}{9} + C}\)(\(C\) は積分定数)
以上で解説は終わりです!
対数は高校で初めて習う概念なので、慣れるまでは少し大変かもしれません。
指数との関係や対数計算のコツをつかんで、ぜひマスターしてくださいね!






