この記事では、「逆関数」の意味や求め方を、豊富な計算問題を通してわかりやすく解説します。
また、逆関数の微分・積分の公式についても説明しますので、この記事を通してぜひマスターしてくださいね!
目次
逆関数とは?
逆関数とは、変数同士の対応関係を逆にした関数です。
例えば、\(1\) を入力すると \(3\) を出力する関数 \(f\) があるとします。
このとき、入出力を入れ替えて、 \(3\) を入力すると \(1\) を出力する関数が \(f\) の逆関数であり、\(\color{red}{f^{−1}}\) (エフインバース)と表します。

このように、イメージとしてはシンプルな逆関数ですが、定義を言葉で書くと少し難しく感じるかもしれません。
【復習】関数の定義
まずは関数の定義を確認してから、逆関数の定義を説明していきます。
\(x\) に対して \(y\) が規則 \(f\) によってただ \(1\) つに定まるとき、\(f\) を「関数」といい、\(y = f(x)\) と表せる。
特に、\(y\) に対して \(x\) がただ \(1\) つに定まるとき \((x_1 \neq x_2\) \(\Rightarrow\) \(f(x_1) \neq f(x_2))\)、\(y = f(x)\) は「\(1\) 対 \(1\) の関数」であるという。

\(x\) に対して \(y\) が \(1\) つに定まることが関数の条件です。
一方で、\(1\) つの \(y\) に対して複数の \(x\) が対応しても構わないのでした。二次関数や三次関数などがいい例ですね。
逆関数の定義
関数の定義を踏まえた上で、逆関数の定義は次のとおりです。
\(x\) の関数 \(y = f(x)\) において、\(y\) の値を定めると \(x\) の値がただ \(1\) つに定まるとき、すなわち、\(x\) が \(y\) の関数として \(x = g(y)\) と表されるとき、その変数 \(x\), \(y\) を入れ替えた \(\color{red}{y = g(x)}\) を \(\color{red}{y = f(x)}\) の逆関数といい、\(\color{red}{f^{−1}(x)}\) で表す。
すべての関数が逆関数をもてるわけではなく、逆関数をもてるのは \(1\) 対 \(1\) の関数だけということですね。
実際の問題では、全体としては \(1\) 対 \(1\) の関数ではなくても、\(1\) 対 \(1\) になるように定義域を絞った部分の逆関数を求めることがよくあります。
基本的には、単調増加または単調減少の部分なら逆関数を求められると認識しておきましょう。
逆関数の性質
逆関数には、いくつかの重要な性質があります。
関数 \(f(x)\) の逆関数 \(f^{−1}(x)\) について、以下が成り立つ。
- \(b = f(a) \iff a = f^{−1}(b)\)
- \(f(x)\) と \(f^{−1}(x)\) では、定義域と値域が入れ替わる
- \(y = f(x)\) と \(y = f^{−1}(x)\) のグラフは、直線 \(y = x\) について対称である
逆関数は入力 \(x\) と出力 \(y\) の関係を入れ替えたものですから、どれも成り立つことがわかりますね。
また、性質 3 は逆関数のグラフを書く際に利用するので押さえておきましょう!
ちなみに、逆関数の逆関数は元の関数になります。
カードを裏返してもう一度裏返すことと一緒なので、当たり前ですね。
逆関数の求め方【例題】
次の例題を通して、ある関数の逆関数を求める方法を説明します。
関数 \(\displaystyle y = \frac{3}{x} + 2\) \((x > 0)\) の逆関数を求めよ。
逆関数は、次の手順で求められます。
まずは、与えられた関数の値域を求めます。
元の関数の値域は、求める逆関数の定義域になるので必ず確認してください。
\(\displaystyle y = \frac{3}{x} + 2\) \((x > 0)\) の値域は \(y > 2\)
次に、元の関数を「\(x =\) ~」の形に変形します。
\(\displaystyle y = \frac{3}{x} + 2\) を \(x\) について解くと、
\(\displaystyle \frac{3}{x} = y − 2\)
\(\displaystyle \frac{1}{x} = \frac{y − 2}{3}\)
\(y > 2\) より、両辺の逆数をとって
\(\displaystyle x = \frac{3}{y − 2}\)
最後に、\(x\) と \(y\) を入れ替えれば逆関数のできあがりです!
最初に求めた値域の \(y\) も \(x\) に入れ替えて、定義域としてくださいね。
よって、求める逆関数は
\(\color{red}{\displaystyle y = \frac{3}{x − 2}}\) \(\color{red}{(x > 2)}\)
ちなみに、元の関数と逆関数をグラフに書くと次のようになります。
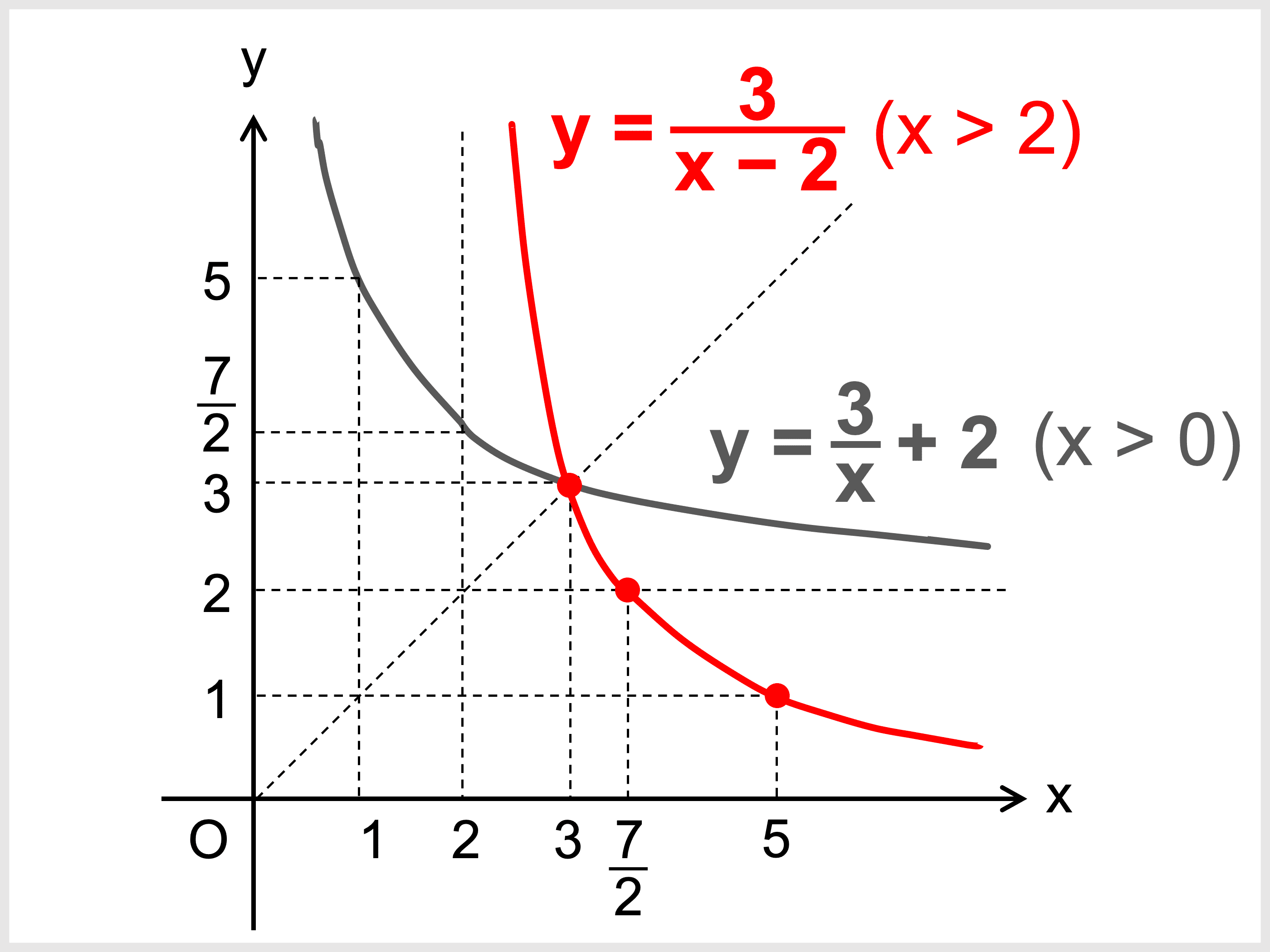
確かに \(y = x\) について対称になっていますね。
「分数関数」のグラフの書き方は、以下の記事で解説しています。
 分数関数とは?グラフの書き方、分数不等式、微分積分を解説
分数関数とは?グラフの書き方、分数不等式、微分積分を解説
逆関数の計算問題
それでは、逆関数の計算問題に挑戦しましょう。
計算問題①「対数関数の逆関数とグラフを求める」
次の関数の逆関数を求め、両方のグラフを書け。
\(y = \log_3 (x + 2) \,\,\) \((1 \leq x \leq 7)\)

対数と指数の関係に注意しながら、逆関数を求めましょう。
対数関数の逆関数が指数関数であることを再確認できますよ。
\(y = \log_3 (x + 2)\,\, \) \((1 \leq x \leq 7)\) …①
とする。
①の値域は、\(1 \leq y \leq 2\)
①を \(x\) について解くと、
\(3^y = x + 2\)
\(x = 3^y − 2\)
よって求める逆関数は、
\(y = 3^x − 2 \,\,\) \((1 \leq x \leq 2)\)
グラフは次の通り。
答え: \(\color{red}{y = 3^x − 2}\,\,\) \(\color{red}{(1 \leq x \leq 2)}\)

計算問題②「元の関数と逆関数が一致する」
関数 \(\displaystyle y = \frac{ax + b}{x + 2}\,\,\) \((b \neq 2a)\) のグラフは点 \((1, 1)\) を通り、また、この関数の逆関数は元の関数と一致する。このとき、定数 \(a, b\) の値を求めよ。

(元の関数) = (逆関数) という条件式が、\(x\) の恒等式となることを示しましょう。
\(\displaystyle y = \frac{ax + b}{x + 2}\) …① とする。
①は点 \((1, 1)\) を通るから
\(\displaystyle 1 = \frac{a + b}{3}\)
\(a + b = 3\)
よって \(b = 3 − a\) …②
ここで、
\(\begin{align}\displaystyle \frac{ax + b}{x + 2} &= \frac{a(x + 2) − 2a + b}{x + 2} \\&= a + \frac{b − 2a}{x + 2}\end{align}\)
\(b \neq 2a\) より、①の値域は \(y \neq a\)
①を変形して
\(y(x + 2) = ax + b\)
\(x(y − a) = −2y + b\)
\(y \neq a\) より \(\displaystyle x = \frac{−2y + b}{y − a}\)
したがって、①の逆関数は
\(\displaystyle y = \frac{−2x + b}{x − a}\) \((x \neq a)\) …③
①と③が一致するには、
\(\displaystyle \frac{ax + b}{x + 2} = \frac{−2x + b}{x − a}\) が \(x\) の恒等式となればよい。
両辺の定義域から、分母を払うことができ
\((ax + b)(x − a) = (−2x + b)(x + 2)\)
両辺を展開して
\(\begin{align}ax^2 + &(−a^2 + b)x − ab \\&= −2x^2 + (−4 + b)x + 2b\end{align}\)
両辺の係数を比較して
\(a = −2\)
\(−a^2 + b = −4 + b\)
\(−ab = 2b\)
\(a = −2\) を②に代入すると \(b = 3 − (−2) = 5\)
したがって、\(a = −2, b = 5\)
答え: \(\color{red}{a = −2, b = 5}\)
逆関数の微分法【公式】
逆関数を利用して、ある関数を微分する方法があります。
\(y = f(x)\) の逆関数を \(y = f^{−1}(x)\) とすると、
\begin{align} x = f(y) \end{align}
両辺を \(x\) で微分すると、
\begin{align} 1 &= \frac{df(y)}{dx} \\&= \frac{df(y)}{dy} \cdot \frac{dy}{dx} \end{align}
\(x = f(y)\) より
\begin{align} 1 = \frac{dx}{dy} \cdot \frac{dy}{dx} \end{align}
したがって
\begin{align} \frac{dy}{dx} = \frac{1}{\frac{dx}{dy}} \end{align}
逆関数の微分法は、次のような場合に利用できることがあります。
- \(y\) を \(x\) で微分するよりも、\(x\) を \(y\) で微分する方が楽
- \(y = f(x)\) の形にできない関数を微分したい
例題を見てみましょう。
例題①「逆関数の微分を利用する」
\(x = 2y^2 − 4y + 1\) について、\(\displaystyle \frac{dy}{dx}\) を \(x\) の関数であらわせ。
「\(x =\) ~」の形になっているので、\(\displaystyle \frac{dx}{dy}\) を求めてから逆数をとる方が楽ですね。
\(\displaystyle \frac{dx}{dy} = 4y − 4\) より、
\(\begin{align} \frac{dy}{dx} &= \frac{1}{\frac{dx}{dy}} \\ &= \frac{1}{4y − 4} \\ &= \frac{1}{4(y − 1)} \end{align}\)
ここで、\(x = 2y^2 − 4y + 1\) を \(y\) について解くと、
\(2y^2 − 4y + 1 − x = 0\)
\(2(y − 1)^2 − 1 − x = 0\)
\(2(y − 1)^2 = x + 1\)
\(\displaystyle (y − 1)^2 = \frac{x + 1}{2}\)
\(\displaystyle y − 1 = \pm \sqrt{\frac{x + 1}{2}}\)
よって
\(\begin{align} \frac{dy}{dx} &= \frac{1}{4(y − 1)} \\ &= \pm \frac{1}{4} \sqrt{\frac{2}{x + 1}} \\ &= \pm \frac{\sqrt{2}}{4\sqrt{x + 1}}\end{align}\)
答え: \(\color{red}{\displaystyle \frac{dy}{dx} = \pm \frac{\sqrt{2}}{4\sqrt{x + 1}}}\)
この問題は、逆関数の微分を利用せず「\(y =\) ~」の形に直してからそのまま微分することもできます。
例題②「\(\sin\) の逆関数を微分する」
次の関数について、\(\displaystyle \frac{dy}{dx}\) を \(x\) の関数で表せ。
\(x = \sin y\) \(\left(\displaystyle −\frac{\pi}{2} < y < \frac{\pi}{2}\right)\)
三角関数の逆関数は、高校の知識では「\(y =\) ~」の形に変形できません。
そこで、\(\displaystyle \frac{dx}{dy}\) を求めてから逆数をとって \(\displaystyle \frac{dy}{dx}\) を求めましょう。
\(\displaystyle \frac{dx}{dy} = \cos y\)
また、\(\displaystyle −\frac{\pi}{2} < y < \frac{\pi}{2}\) より \(0 < \cos y\) であるから
\(\begin{align} \frac{dy}{dx} &= \frac{1}{\frac{dx}{dy}} \\ &= \frac{1}{\cos y} \\ &= \frac{1}{\sqrt{1 − \sin^2 y}} \\ &= \frac{1}{\sqrt{1 − x^2}} \end{align}\)
答え: \(\color{red}{\displaystyle \frac{dy}{dx} = \frac{1}{\sqrt{1 − x^2}}}\)
置換積分のテクニックで、\(a^2 − x^2\) を含む関数は \(x = a \sin\theta\) に置換するとうまくいく、というものがありました。
この問題で示したように、実は逆関数の微分・積分の考え方が裏にあるのです。
\(x^2 + a^2\) を含む関数で \(x = a \tan\theta\) に置換する根拠も同様に示すことができます。
気になる人は計算してみてくださいね!
 置換積分法の公式やパターンを見分けるコツをわかりやすく解説
置換積分法の公式やパターンを見分けるコツをわかりやすく解説
逆関数の積分法【公式】
逆関数を利用して、ある関数を積分する方法があります。
\(y = f(x)\) の逆関数を \(y = f^{−1}(x)\) とすると、
\begin{align} x = f(y) \end{align}
両辺を \(x\) で微分すると、
\begin{align} 1 &= \frac{df(y)}{dx} \\ &= \frac{df(y)}{dy} \cdot \frac{dy}{dx} \\ &= f’(y) \cdot \frac{dy}{dx} \end{align}
よって
\begin{align} \frac{1}{f’(y)} = \frac{dy}{dx} \end{align}
両辺を \(x\) で積分して
\begin{align} \int \frac{1}{f’(y)} \ dx &= \int \frac{dy}{dx} \ dx \\ &= \int dy \\ &= y + C \\ &= f^{−1}(x) + C \end{align}
逆関数の積分法は、次のような場合に利用できることがあります。
- \(y\) を \(x\) で積分するよりも、\(x\) を \(y\) で積分する方が楽
- \(y = f(x)\) の形にできない関数を積分したい
例題を見てみましょう。
例題「\(\tan^{−1} x\) を積分する」
\(y = \tan x\) \(\left(\displaystyle −\frac{\pi}{2} < x < \frac{\pi}{2}\right)\) の逆関数は \(y = \tan^{−1} x\) と表される。
\(\displaystyle \int_1^{\sqrt{3}} \tan^{−1} x \ dx\) を求めよ。
高校では \(\tan^{−1} x\) の積分公式を習わないので、直接積分できません。
そこで、逆関数 \(\tan\) の導関数を利用して、置換積分で解いていきます。
\(y = \tan^{−1} x\) のとき、\(x = \tan y\)
両辺を \(y\) で微分すると
\(\displaystyle \frac{dx}{dy} = \frac{1}{\cos^2 y}\)
\(\displaystyle dx = \frac{1}{\cos^2 y} \ dy\)
| \(x\) | \(1 \longrightarrow \sqrt{3}\) |
| \(y\) | \(\displaystyle \frac{\pi}{4} \longrightarrow \displaystyle \frac{\pi}{3}\) |
よって
\(\displaystyle \int_1^{\sqrt{3}} \tan^{−1} x \, dx\)
\(\displaystyle = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} y \cdot \frac{1}{\cos^2y} \, dy\)
\(\displaystyle = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} y \cdot (\tan y)’ \, dy\)
\(\displaystyle = \left[ y \cdot \tan y \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} − \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \tan y \, dy\)
ここで、
\(\begin{align} \int \tan y \, dy &= \int \frac{\sin y}{\cos y} \ dy \\ &= −\int \frac{(\cos y)’}{\cos y} \ dy \\ &= − \log|\cos y| + C \end{align}\)
より
\(\displaystyle \left[ y \cdot \tan y \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} − \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \tan y \ dy\)
\(\displaystyle = \left[ y \cdot \tan y \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} − \left[−\log|\cos y|\right]_{\frac{\pi}{4}}^{\frac{\pi}{3}}\)
\(\displaystyle = \left(\frac{\pi}{3} \cdot \sqrt{3} − \frac{\pi}{4} \cdot 1\right) − \left( −\log |\cos \frac{\pi}{3}| + \log |\cos \frac{\pi}{4}| \right)\)
\(\displaystyle = \frac{\sqrt{3}}{3} \pi − \frac{\pi}{4} − \left( −\log \frac{1}{2} + \log \frac{1}{\sqrt{2}} \right)\)
\(\displaystyle = \frac{4\sqrt{3} − 3}{12} \pi + \log 2^{−1} − \log 2^{−\frac{1}{2}}\)
\(\displaystyle = \frac{4\sqrt{3} − 3}{12} \pi + \log2^{−\frac{1}{2}}\)
\(\displaystyle = \frac{4\sqrt{3} − 3}{12} \pi − \frac{1}{2} \log{2}\)
答え: \(\color{red}{\displaystyle \int_1^{\sqrt{3}} \tan^{−1} x \ dx = \frac{4\sqrt{3} − 3}{12} \pi − \frac{1}{2} \log{2}}\)
【参考】三角関数の逆関数
高校では習いませんが、三角関数の逆関数には「arc(アーク)」という言葉をつけて表します。
逆三角関数は、次のように表せる。
- \(y = \sin x\) \(\left(\displaystyle −\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\right)\) の逆関数
\begin{align}\color{red}{y = \sin^{−1} x = \arcsin x}\end{align} - \(y = \cos x\) \(\left(0 \leq x \leq \pi\right)\) の逆関数
\begin{align}\color{red}{y = \cos^{−1} x = \arccos x}\end{align} - \(y = \tan x\) \(\left(\displaystyle −\frac{\pi}{2} < x < \frac{\pi}{2}\right)\) の逆関数
\begin{align}\color{red}{y = \tan^{−1} x = \arctan x}\end{align}
三角関数は周期関数のため \(1\) 対 \(1\) の関数ではありませんが、定義域を制限すれば逆関数を定義できます。
\(\sin^{−1} x\) と \(\arcsin x\)、どちらの書き方も一般的によく使われるので、知っておいて損はありません。
ちなみに、それぞれのグラフは次のようになります。

以上で逆関数の解説は終わりです!
なんとなく複雑に思える逆関数ですが、性質を理解しておけば怖くありません。
しっかりとマスターしてくださいね!

