この記事では、「合成関数」についてわかりやすく解説していきます。
関数を合成するやり方や、合成関数の微分・積分の公式とやり方などを説明しますので、この記事を通してぜひマスターしてくださいね!
合成関数とは?
合成関数とは、ある関数に別の関数を組み込んだ(合成した)関数のことです。
\(2\) つの関数 \(y = f(x)\), \(z = g(y)\) があり、\(f(x)\) の値域が \(g(y)\) の定義域に含まれているとき、\(g(y)\) に \(y = f(x)\) を代入して得られる関数 \(\color{red}{z = g(f(x))}\) を「\(f(x)\) と \(g(y)\) の合成関数」といい、\(\color{red}{(g \circ f)(x)}\) と表す。
すなわち
\begin{align} \color{red}{(g \circ f)(x) = g(f(x)) }\end{align}

関数の合成は、変数を入れる箱に別の関数を代入するイメージですね。
このとき、変数の文字に神経質になる必要はありません。
とにかく、ある関数の変数の部分に別の関数を組み込むんだ、と理解しておきましょう。
合成関数の性質
合成関数には、次の \(4\) つの重要な性質が成り立ちます。
関数の合成について、次のことが言える。
- 交換法則は一般には成り立たない。
\begin{align}\color{red}{ (g \circ f)(x) \neq (f \circ g)(x) }\end{align}
- 結合法則は成り立つ。
\begin{align}\color{red}{ (h \circ (g \circ f))(x) = ((h \circ g) \circ f)(x) }\end{align}
- 関数 \(f\) が逆関数 \(f^{−1}\) をもつとき、それらを合成した関数は恒等関数(※)となる。
\begin{align}\color{red}{ (f^{−1} \circ f)(x) = (f \circ f^{−1})(x) = x }\end{align}
※ 変数 \(x\) に \(x\) 自身を対応させる関数。
- 合成関数の逆関数は、それぞれの逆関数を逆向きに合成した関数に等しい。
関数 \(f, g\) がそれぞれ逆関数 \(f^{−1}\), \(g^{−1}\) をもつとき、次が成り立つ。
\begin{align}\color{red}{ (g \circ f)^{−1}(x) = (f^{−1} \circ g^{−1})(x) }\end{align}
それぞれ詳しく見ていきましょう。
【性質1】交換法則の不成立
一般に、合成の順序を入れ替えると異なる関数になってしまいます。

(例)
\(f(x) = x + 2\), \(g(x) = 2x − 1\)
\(\begin{align}(g \circ f)(x) &= g(f(x)) \\&= 2(x + 2) − 1 \\&= 2x + 3\end{align}\)
\(\begin{align}(f \circ g)(x) &= f(g(x)) \\&= (2x − 1) + 2 \\&= 2x + 1\end{align}\)
よって \((g \circ f)(x) \neq (f \circ g)(x)\)
そのため、合成関数を求めるときは合成する関数とされる関数の関係性に常に注意を払いましょう。
【性質2】結合法則の成立
\(3\) つ以上の関数を合成することもでき、合成する方とされる方の関係性さえ守れていれば、どの部分から合成しても構いません。

(例)
\(f(x) = x + 2\), \(g(x) = 2x − 1\), \(h(x) = −x^2\)
\((g \circ f)(x) = 2x + 3\) より、
\((h \circ (g \circ f))(x) = −(2x + 3)^2\)
また、\((h \circ g)(x) = −(2x − 1)^2\) より、
\(\begin{align}((h \circ g) \circ f)(x) &= −\{2(x + 2) − 1\}^2 \\&= −(2x + 3)^2\end{align}\)
よって
\((h \circ (g \circ f))(x) = ((h \circ g) \circ f)(x)\)
結合法則が成り立つことから、内側の括弧を省略して \(\color{red}{(h \circ g \circ f)(x)}\) と表すこともできます。
【性質3】関数と逆関数の合成関数
ある関数 \(f\) とその逆関数 \(f^{−1}\) を合成すると、恒等関数(ある変数を入れると、それ自身を返す関数)になります。
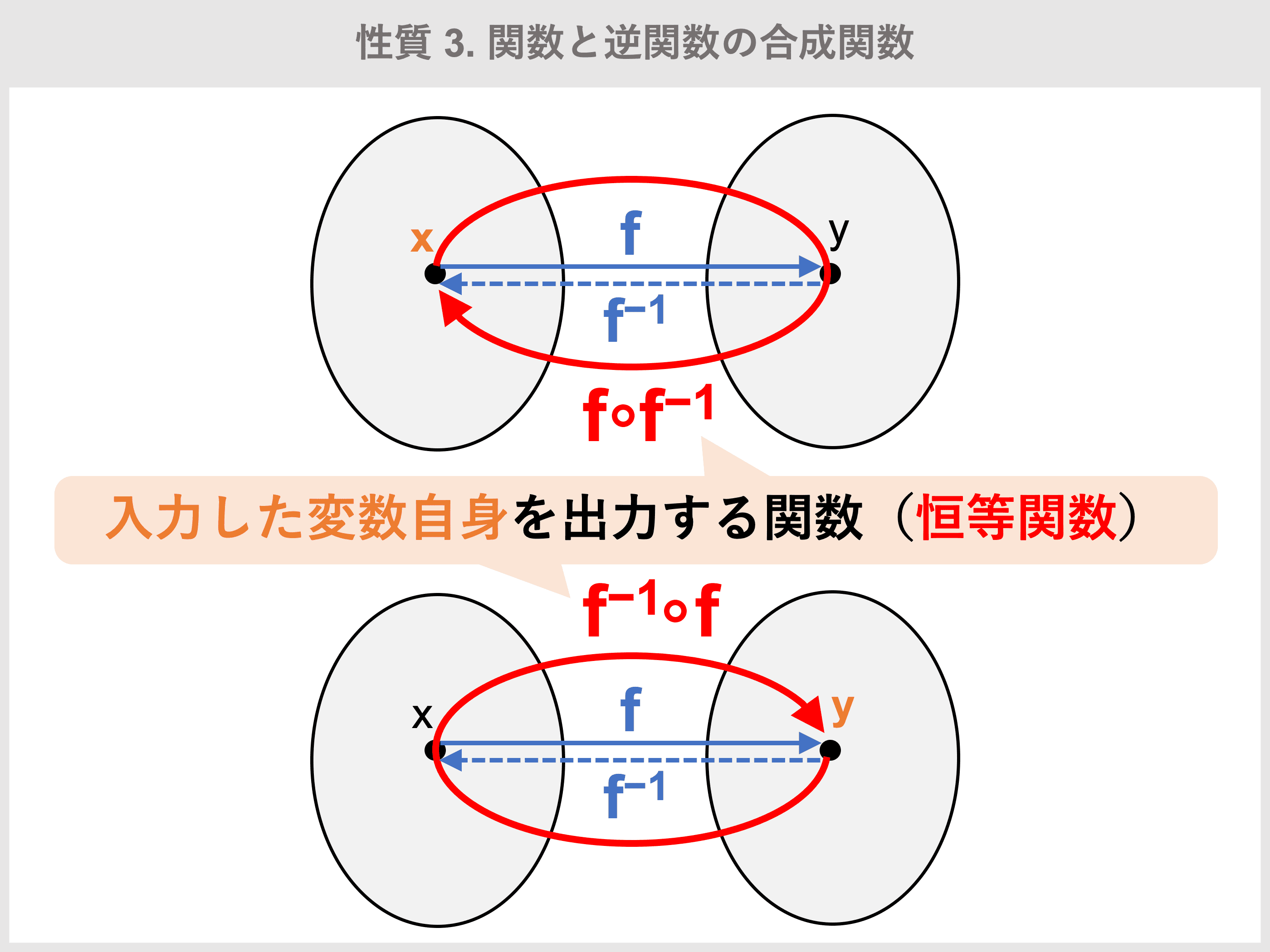
この性質が成り立つ理由は以下の通りです。
\(y = f(x) \iff x = f^{−1}(y)\) より
\((f^{−1} \circ f)(x) = f^{−1}(f(x)) = f^{−1}(y) = x\)
同様に、
\((f \circ f^{−1})(y) = f(f^{−1}(y)) = f(x) = y\)
\(y\) を \(x\) に置き換えると \((f \circ f^{−1})(x) = x\)
よって
\((f^{−1} \circ f)(x) = (f \circ f^{−1})(x) = x\)
【性質4】合成関数の逆関数
合成関数の逆関数は、個々の逆関数を逆向きに合成した関数に等しくなります。

合成の順序が逆になることに注意しましょう。
(例)
\(f(x) = x − 3\), \(g(x) = \sqrt{x}\)
\((g \circ f)(x) = \sqrt{x − 3}\) より
\((g \circ f)^{−1}(x) = x^2 + 3\)
また、
\(f^{−1}(x) = x + 3\)
\(g^{−1}(x) = x^2\)
より
\((f^{−1} \circ g^{−1})(x) = (x^2) + 3 = x^2 + 3\)
よって、
\((g \circ f)^{−1}(x) = (f^{−1} \circ g^{−1})(x)\)
関数の合成のやり方
次の例題を通して、合成関数を求める方法を説明します。
(1) \(f(x) = x + 2\), \(g(x) = x^2 + 2x − 1\) のとき、\((g \circ f)(x)\) を求めよ。
(2) \(f(x) = 3^x\), \(g(x) = \log_9 x\) のとき、\((f \circ g)(x)\) を求めよ。
合成関数の表記にしたがって、前者の関数の変数部分に後者の関数を代入します。
(1) は \((g \circ f)(x) = g(f(x))\) なので、\(g(\color{salmon}{x})\) の変数部分 \(\color{salmon}{x}\) に \(f(x)\) を代入します。
一方、(2) は \((f \circ g)(x) = f(g(x))\) なので、\(f(\color{salmon}{x})\) の変数部分 \(\color{salmon}{x}\) に \(g(x)\) を代入します。
(1)
\(\begin{align} (g \circ f)(x) &= g(f(x)) \\ &= (f(x))^2 + 2(f(x)) − 1 \\ &= (x + 2)^2 + 2(x + 2) − 1 \\ &= x^2 + 4x + 4 + 4x + 4 − 1 \\ &= x^2 + 8x + 7\end{align}\)
答え: \(\color{red}{(g \circ f)(x) = x^2 + 8x + 7}\)
(2)
\(\begin{align} (f \circ g)(x) &= f(g(x)) \\ &= 3^{g(x)} \\ &= 3^{\log_9 x} \\ &= 3^{\frac{\log_3 x}{\log_3 9}} \\ &= 3^{\frac{1}{2} \log_3 x} \\ &= 3^{\log_3 \sqrt{x}} \\ &= \sqrt{x} \end{align}\)
答え: \(\color{red}{(f \circ g)(x) = \sqrt{x}}\)
コツをつかめば難しくないですね!
関数の合成を知っていると、複雑な関数を簡単な関数同士を合成したものと見ることができ、便利な場面が出てきます。
練習問題「関数を合成する」
もう少し複雑な問題で、関数の合成を練習しましょう。
次の関数 \(f(x)\), \(g(x)\), \(h(x)\) について、以下の問いに答えよ。
\(f(x) = x − 1\), \(g(x) = \log_2 x\), \(h(x) = \sin x\)
(1) 合成関数 \((g \circ f)(x)\)、およびその定義域と値域を求めよ。
(2) 合成関数 \(((h \circ g) \circ f)(x)\) を求めよ。
(3) 合成関数 \((f^{−1} \circ g^{−1})(x)\) を求めよ。

合成関数の性質に注目すると、(1) の結果を (2)(3) にうまく生かすことができます。
(1)
\((g \circ f)(x) = g(f(x)) = \log_2 (x − 1)\)
真数は常に正であるから
\(x − 1 > 0\) すなわち \(1 < x\)
また、対数 \(\log_2 (x − 1)\) の値域は実数全体である。
答え:
\(\color{red}{(g \circ f)(x) = \log_2 (x − 1)}\)
定義域は \(\color{red}{1 < x}\)、値域は実数全体
(2)
(1) より、
\(\begin{align}((h \circ g) \circ f)(x) &= (h \circ (g \circ f))(x) \\&= \sin(\log_2 (x − 1))\end{align}\)
答え: \(\color{red}{((h \circ g) \circ f)(x) = \sin(\log_2 (x − 1))}\)
(3)
\((f^{−1} \circ g^{−1})(x) = (g \circ f)^{−1}(x)\)
(1) より
\((g \circ f)(x) = \log_2 (x − 1)\) であるから
\(y = \log_2 (x − 1)\) とおくと
\(2^y = x − 1\)
\(x = 2^y + 1\)
よって \((g \circ f)^{−1}(x) = 2^x + 1\)
したがって、
\((f^{−1} \circ g^{−1})(x) = (g \circ f)^{−1}(x) = 2^x + 1\)
答え: \(\color{red}{(f^{−1} \circ g^{−1})(x) = 2^x + 1}\)
合成関数の微分法【公式】
合成関数を微分する公式は次のとおりです。
\(y\) が \(u\) の関数で、\(u\) が \(x\) の関数であるとき、\(y\) を \(x\) について微分すると
\begin{align}\color{red}{\displaystyle \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}}\end{align}
\(y = f(u)\), \(u = g(x)\) とおくと
\begin{align}\color{red}{\{f(g(x))\}’ = f’(g(x)) g’(x)}\end{align}
\(u = g(x)\) を箱とみて、\(\bf{(\text{全体を箱について微分}) \times (\text{箱の中身を微分})}\) をすると覚えておきましょう。
合成関数の微分公式を覚えるのはそれほど難しくありませんが、対象の関数が合成関数であると判断する力が必要です。
公式の証明は以下の記事で説明しています。
 微分公式の証明一覧!導関数の定義どおりの導出を解説
微分公式の証明一覧!導関数の定義どおりの導出を解説
合成関数の微分のやり方
次の例題を通して、合成関数の微分のやり方を説明します。
関数 \(y = (x − 3)^3\) を微分せよ。
右辺を展開すればそのまま通常の微分ができますが、三次式の展開は少し面倒です。
そこで、合成関数と考えて微分していきます。
まずは、どんな関数同士が合成されているかを見極めます。
慣れるまでは、関数を組み込む変数部分を箱(\(□\))で考えるとわかりやすいです。
関数 \(y = (x − 3)^3\) においては、べき乗の中身を \(1\) つの箱と見ると、
- \(y = □^3\)
- \(□ = x − 3\)
という \(2\) つの関数が合成されていると考えられますね。
合成関数を微分するには、\(\bf{(\text{全体を箱について微分}) \times (\text{箱の中身を微分})}\) をします。
つまり、「\(□^3\) を \(□\) について微分」「\(x − 3\) を \(x\) について微分」し、かけ合わせます。
\(y = (x − 3)^3\) より、
\(\begin{align} y’ &= 3(x − 3)^2 \cdot (x − 3)’ \\ &= 3(x − 3)^2 \cdot 1 \\ &= 3(x − 3)^2 \end{align}\)
答え: \(\color{red}{y’ = 3(x − 3)^2}\)
以降、様々な種類の合成関数を微分する練習問題に挑戦しましょう。
練習問題①「\(y = \sqrt{x^2 + 2}\) の微分」
関数 \(y = \sqrt{x^2 + 2}\) を微分せよ。

次は、無理関数 \(\sqrt{□}\) に多項式の関数 \(□ = x^2 + 2\) が合成されていますね。
\(y = \sqrt{x^2 + 2} = (x^2 + 2)^{\frac{1}{2}}\) より、
\(\begin{align} y’ &= \frac{1}{2} (x^2 + 2)^{−\frac{1}{2}} \cdot (x^2 + 2)’ \\ &= \frac{1}{2\sqrt{x^2 + 2}} \cdot 2x \\ &= \frac{x}{\sqrt{x^2 + 2}} \end{align}\)
答え: \(\color{red}{y’ = \displaystyle \frac{x}{\sqrt{x^2 + 2}}}\)
練習問題②「\(y = \cos(2x^2 − 1)\) の微分」
関数 \(y = \cos(2x^2 − 1)\) を微分せよ。

三角関数 \(\cos □\) に多項式の関数 \(□ = 2x^2 − 1\) が合成されています。
\(\begin{align} y’ &= −\sin(2x^2 − 1) \cdot (2x^2 − 1)’ \\ &= −4x \sin(2x^2 − 1)\end{align}\)
答え: \(\color{red}{y’ = −4x \sin(2x^2 − 1)}\)
練習問題③「\(y = \log(\sin(e^x + 2))\) の微分」
関数 \(y = \log(\sin(e^x + 2))\) を微分せよ。

対数関数 \(\log\)、三角関数 \(\sin\)、指数関数 \(e^x\) の \(3\) つの関数が合成されています。
この場合も考え方は同じで、全体の微分、\(1\) つ中身の微分、さらに \(1\) つ中身の微分を順番にかけ合わせましょう。
\(\begin{align} y’ &= \frac{1}{\sin(e^x + 2)} \cdot \cos(e^x + 2) \cdot e^x \\ &= \frac{e^x \cos(e^x + 2)}{\sin(e^x + 2)} \\ &= \frac{e^x}{\tan(e^x + 2)} \end{align}\)
答え: \(\color{red}{\displaystyle y’ = \frac{e^x}{\tan(e^x + 2)}}\)
合成関数の微分には慣れましたか?
数IIIの微分法ではとてもよく登場するので、必ず理解しておきましょう!
合成関数の積分法【公式】
合成関数を積分する際は、以下の公式を用います。
関数 \(f\) の原始関数の \(1\) つを \(F\) とすると、
\begin{align}\color{red}{ \int f(g(x)) g’(x) \ dx = F(g(x)) + C }\end{align}
(\(C\) は積分定数)
特に、関数 \(f\) がべき乗関数の場合 (\(f(u) = u^{\alpha}\))、
- \(\alpha \neq −1\) のとき
\begin{align}\color{red}{\displaystyle \int \{g(x)\}^{\alpha} g’(x) \ dx = \frac{\{g(x)\}^{\alpha + 1}}{\alpha + 1} + C }\end{align} - \(\alpha = −1\) のとき
\begin{align}\color{red}{ \int \{g(x)\}^{−1} g’(x) \ dx} & \color{red}{= \int \frac{g’(x)}{g(x)} \ dx} \\&\color{red}{= \log|g(x)| + C }\end{align}
また、合成されている中身が一次式程度の簡単な関数であれば、中身の微分を無理やり作り出して積分することができます。
関数 \(f\) の原始関数の \(1\) つを \(F\) とすると、\(a \neq 0\) のとき
\begin{align}&\displaystyle \int f(ax + b) \ dx \\ &= \frac{1}{(ax + b)’} \int f(ax + b) \cdot (ax + b)’ \ dx \\&= \color{red}{\frac{1}{a} F(ax + b) + C}\end{align}
合成関数の積分のしくみ
合成関数の積分は、合成関数の微分を逆向きにやればよいということになります。
つまり、積分したい関数を合成関数と見たときに、合成された中身の微分がいれば、全体を積分できます。

なぜこのように積分できるかは、「置換積分法」の考え方で説明できます。
 置換積分法の公式やパターンを見分けるコツをわかりやすく解説
置換積分法の公式やパターンを見分けるコツをわかりやすく解説
合成関数の積分のやり方
次の不定積分を求めよ。
\(\displaystyle \int \frac{6x + 1}{3x^2 + x − 5} \ dx\)
合成関数の積分では、「問題を合成関数の積分ととらえる力」「中身の微分を見つける力」がカギになります。
まずは、合成関数における箱 \(□\) とその中身の微分を特定します。
特に、多項式が含まれる関数では、次数が \(\bf{1}\) ずつ下がったかたまりがいないか確認します。
この問題では、関数 \((3x^2 + x − 5)\) の微分 \((3x^2 + x − 5)’ = 6x + 1\) が分子にありますね。
よって、
\(\left\{\begin{array}{l} y = \displaystyle \frac{1}{□}\\ □ = 3x^2 + x − 5\end{array}\right.\) の合成関数で、
\(□\)の中身の微分 \((3x^2 + x − 5)’\) がある
と判断できます。
合成関数と中身の微分が特定できたら、合成関数を積分します。
今回は、公式 \(\displaystyle \int \frac{g’(x)}{g(x)} \ dx = \log|g(x)| + C\) のかたちですね。
\(\displaystyle \int \frac{6x + 1}{3x^2 + x − 5} \ dx\)
\(\displaystyle = \int \frac{(3x^2 + x − 5)’}{3x^2 + x − 5} \ dx\)
\(= \log|3x^2 + x − 5| + C\)
答え: \(\color{red}{\log|3x^2 + x − 5| + C}\)(\(C\) は不定積分)
\(\displaystyle \frac{\text{(多項式)}}{\text{(多項式)}}\) の形をしている関数は「分数関数」と呼ばれます。
 分数関数とは?グラフの書き方、分数不等式、微分積分を解説
分数関数とは?グラフの書き方、分数不等式、微分積分を解説
以降、様々な種類の合成関数を積分する練習問題に挑戦しましょう。
練習問題①「\(\displaystyle \int \sin^3 x \cos x \ dx\)」
次の不定積分を求めよ。
\(\displaystyle \int \sin^3 x \cos x \ dx\)

\((\sin x)’ = \cos x\) なので、\(f(u) = u^3\) に \(g(x) = \sin x\) を合成した関数の積分と見ることができますね。
\(\displaystyle \int \sin^3 x \cos x \ dx\)
\(\displaystyle = \int (\sin x)^3 \cdot (\sin x)’ \ dx\)
\(\displaystyle = \frac{1}{4} \sin^4 x + C\)
答え: \(\displaystyle \color{red}{\frac{1}{4} \sin^4 x + C}\)(\(C\) は不定積分)
練習問題②「\(\displaystyle \int f(ax + b) \ dx\)」
次の不定積分を求めよ。
(1) \(\displaystyle \int \sqrt{2x − 3} \ dx\)
(2) \(\displaystyle \int \cos \left( \frac{2}{3} x − 1 \right) \ dx\)

ある関数 \(f(u)\) に一次式 \(u = ax + b\) が合成されている場合、微分形 \((ax + b)’\) がなくても無理やり作り出して積分することができます。
もちろん、公式 \(\displaystyle \int f(ax + b) \ dx = \frac{1}{a} F(ax + b) + C\) をそのまま使っても構いません。
(1)
\(\displaystyle \int \sqrt{2x − 3} \ dx\)
\(\displaystyle = \color{salmon}{\frac{1}{2}} \int \sqrt{2x − 3} \cdot \color{salmon}{2}\, dx\)
\(\displaystyle = \color{salmon}{\frac{1}{2}} \int (2x − 3)^{\frac{1}{2}} \cdot \color{salmon}{(2x − 3)’} \ dx\)
\(\displaystyle = \frac{1}{2} \cdot \frac{2}{3} (2x − 3)^{\frac{3}{2}} + C\)
\(\displaystyle = \frac{1}{3} (2x − 3)\sqrt{2x − 3} + C\)
答え: \(\displaystyle \color{red}{\frac{1}{3} (2x − 3)\sqrt{2x − 3} + C}\)(\(C\) は不定積分)
(2)
\(\displaystyle \int \cos \left( \frac{2}{3} x − 1 \right) \ dx\)
\(\displaystyle = \frac{3}{2} \sin \left( \frac{2}{3} x − 1 \right) + C\)
答え:
\(\color{red}{\displaystyle \frac{3}{2} \sin \left( \frac{2}{3} x − 1 \right) + C}\)(\(\color{red}{C}\) は積分定数)
練習問題③「\(\displaystyle \int xe^{−\frac{x^2}{2}} \ dx\)」
次の不定積分を求めよ。
\(\displaystyle \int xe^{−\frac{x^2}{2}} \ dx\)

これも、置換積分法なしで解ける合成関数の積分です。中身の微分が隠れていないか探してみましょう。
\(\displaystyle \left( −\frac{x^2}{2} \right)’ = −x\) より、
\(\displaystyle \int xe^{−\frac{x^2}{2}} dx\)
\(\displaystyle = −\int (−x) e^{−\frac{x^2}{2}} dx\)
\(\displaystyle = −\int \left( −\frac{x^2}{2} \right)’ \cdot e^{−\frac{x^2}{2}} dx\)
\(\displaystyle= −e^{−\frac{x^2}{2}} + C\)
答え: \(\color{red}{\displaystyle −e^{−\frac{x^2}{2}} + C}\)(\(\color{red}{C}\) は積分定数)
以上で問題も終わりです!
合成関数の意味や性質は理解できましたか?
特に、微分・積分の問題では合成関数を見逃さないようにしましょう!


