この記事では、「極限」の公式を一覧でわかりやすく解説していきます。
極限計算のポイントも説明していきますので、ぜひこの記事を通してマスターしてくださいね。
目次
極限とは?
極限とは、注目している対象(数列や関数)がある値(極限値)に限りなく近づくことです。
極限を表すには、英単語 limit からとった「\(\color{red}{\lim}\)」という記号を用います。

\(1\) つ目の式は、数列 \(\{a_n\}\) で \(n\) を無限大にする(= 限りなく大きくする)と第 \(n\) 項の値が限りなく \(0\) に近づくことを表しています。
\(2\) つ目の式は、関数 \(f(x)\) の \(x\) を限りなく \(0\) に近づけると \(f(x)\) の値が限りなく大きくなることを表しています。
極限を考えるのは、大きく分けて数列と関数の \(2\) つの分野です。
それぞれについて見ていきましょう。
数列の極限
数列の極限では、無限数列(\(a_1\), \(a_2\), \(a_3\), \(\cdots\), \(a_n\), \(\cdots\) と項が限りなく続く数列)の第 \(n\) 項が向かう先を考えます。
なお、すべての数列に極限があるわけではありません。
数列の極限の有無は次の通りです。

\(a_n\) が特定の値に収束する場合、および \(\pm\infty\) に発散する場合に、その数列は「極限がある」といいます。
ただし、無限大 \((\pm\infty)\) は値というより「限りなく大きい(または小さい)」という概念なので、「極限値」とは呼びません。注意しましょう!
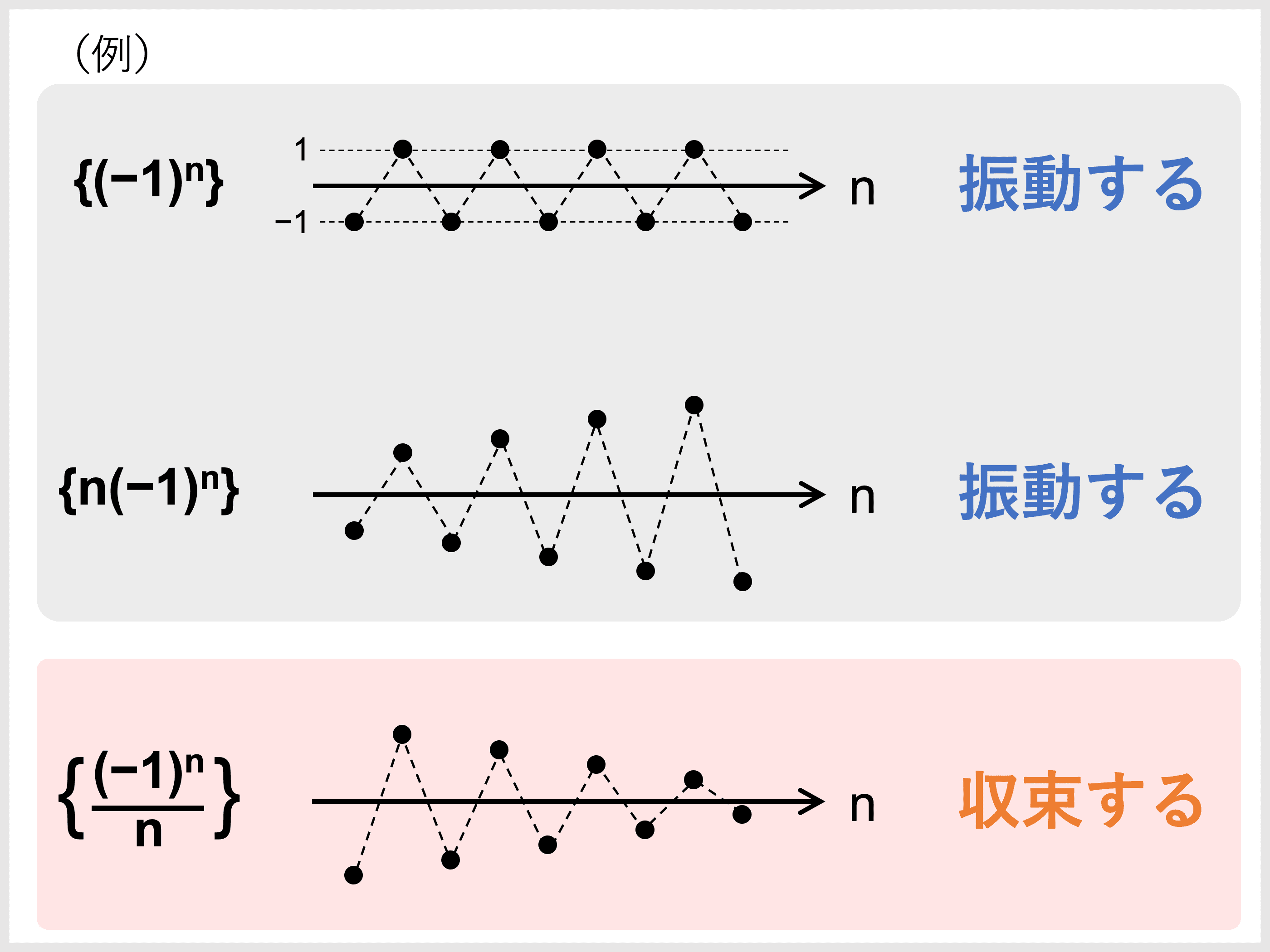
一方で、数列が振動する場合は極限はありません。
振動する数列とは、例えば \(\{(−1)^n\}\) のような数列で、\(n\) をどれだけ大きくしても値が定まらないものです。
一方で、「上下に変化する」 = 「振動する」とは限らないので注意しましょう。
上下の変化がだんだん小さくなり一点に収束していけば、その数列は極限値をもつといえます。
関数の極限
関数の極限では、ある関数 \(f(x)\) の \(x\) に代入する値をどこかに限りなく近づけたときに \(f(x)\) が向かう先を考えます。
数列では \(n \to \infty\) だけを考えますが、関数では \(x \to \pm\infty\), \(x \to a\) (定数) など近づける点がいろいろと選べるのが特徴です。
関数の極限の有無は、数列と同じ考え方で決まります。

一方、関数の極限では近づけ方にも注意が必要です。
数列では \(n \to \infty\)(\(n\) を \(+\) 方向へ)の一方向しか考えませんが、関数では \(x \to a\) としたとき
\(x\) を \(a\) に左側から近づける場合と右側から近づける場合の \(2\) 通りが考えられます。
- 左側極限 \(\displaystyle \lim_{x \to a − 0} f(x)\)
\(x < a\) で、\(x \to a\) のときの \(f(x)\) の極限 - 右側極限 \(\displaystyle \lim_{x \to a + 0} f(x)\)
\(x > a\) で、\(x \to a\) のときの \(f(x)\) の極限
\(\displaystyle \lim_{x \to a − 0} f(x) = \lim_{x \to a + 0} f(x) = \alpha\) \(\iff\) \(\displaystyle \lim_{x \to a} f(x) = \alpha\)
\(\displaystyle \lim_{x \to a − 0} f(x) \neq \lim_{x \to a + 0} f(x)\) のとき、\(\displaystyle \lim_{x \to a} f(x)\) は存在しない

左側極限と右側極限が一致しない場合、全体としては極限がないと捉えるので注意しましょう。
数列の極限公式一覧
ここでは、数列の極限の重要公式を一覧で示します。
数列の極限値の性質
数列の極限において成り立つ計算規則があります。
数列 \(\{a_n\}\), \(\{b_n\}\) が収束して、\(\displaystyle \lim_{n\to\infty} a_n = \alpha\), \(\displaystyle \lim_{n\to\infty} b_n = \beta\) とする。
- 定数倍
\(\displaystyle \lim_{n\to\infty} ka_n = k\alpha\)(\(k\) は定数)
- 和と差
\(\displaystyle \lim_{n\to\infty} (a_n \pm b_n) = \alpha \pm \beta\)
1, 2 を合わせて
\(\displaystyle \lim_{n\to\infty} (ka_n \pm lb_n) = k\alpha \pm l\beta\) (\(k\), \(l\) は定数)
- 積
\(\displaystyle \lim_{n\to\infty} a_nb_n = \alpha\beta\)
- 商
\(\displaystyle \lim_{n\to\infty} \frac{a_n}{b_n} = \frac{\alpha}{\beta}\) (ただし \(\beta \neq 0\))
\(\{n^k\}\) の極限
べき乗の底が無限大に近づくときは次のようになります。
\(k > 0\) のとき
\begin{align}\color{red}{\displaystyle \lim_{n\to\infty} n^k = \infty}\end{align}
\begin{align}\color{red}{\displaystyle \lim_{n\to\infty} \frac{1}{n^k} = 0}\end{align}
無限等比数列 \(\{r^n\}\) の極限
等比数列の極限を考えるときは、公比の範囲に注意する必要があります。
- \(r > 1\) のときは正の無限大に発散する
\(\displaystyle \lim_{n\to\infty} r^n = \infty\) - \(−1 < r \leq 1\) のときは収束する
\(r = 1\) のとき、 \(\displaystyle \lim_{n\to\infty} r^n = 1\)
\(|r| < 1\) のとき、 \(\displaystyle \lim_{n\to\infty} r^n = 0\) - \(r \leq −1\) のときは振動する(極限はない)
なお、「無限級数(無限数列の和)」については以下の記事で詳しく説明しています。
 無限級数、無限等比級数とは?和の公式や求め方、図形問題
無限級数、無限等比級数とは?和の公式や求め方、図形問題
数列の大小関係と極限
数列の大小関係から極限の大小関係を求められることがあります。
特に、追い出しの原理とはさみうちの原理はよく利用するので理解しておきましょう!
十分に大きい \(n\) について \(a_n \leq b_n\) のとき、以下が成り立つ。
- \(\displaystyle \lim_{n\to\infty} a_n = \alpha\), \(\displaystyle \lim_{n\to\infty} b_n = \beta\) ならば \(\alpha \leq \beta\)
- \(\displaystyle \lim_{n\to\infty} a_n = \infty\) ならば \(\displaystyle \lim_{n\to\infty} b_n = \infty\)
(追い出しの原理)
- \(a_n \leq c_n \leq b_n\) のとき \(\displaystyle \lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = \alpha\) ならば \(\displaystyle \lim_{n\to\infty} c_n = \alpha\)
(はさみうちの原理)
「はさみうちの原理」を使う問題の解き方については、以下の記事で詳しく説明しています。
 はさみうちの原理とは?使い方やコツをわかりやすく解説!
はさみうちの原理とは?使い方やコツをわかりやすく解説!
関数の極限公式一覧
ここでは、関数の極限の重要公式を一覧で示します。
関数の極限値の性質
関数の極限でも、数列の極限と同じような計算規則が成り立ちます。
\(\displaystyle \lim_{x \to a} f(x) = \alpha\), \(\displaystyle \lim_{x \to a} g(x) = \beta\) とする。
- 定数倍
\(\displaystyle \lim_{x \to a} kf(x) = k\alpha\)(\(k\) は定数)
- 和と差
\(\displaystyle \lim_{x \to a} (f(x) \pm g(x)) = \alpha \pm \beta\)
1, 2 を合わせて
\(\displaystyle \lim_{x \to a} (kf(x) \pm lg(x)) = k\alpha \pm l\beta\)(\(k\), \(l\) は定数)
- 積
\(\displaystyle \lim_{x \to a} f(x)g(x) = \alpha\beta\)
- 商
\(\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\alpha}{\beta}\)(ただし \(\beta \neq 0\))
なお、\(x \to a\) を \(x \to \infty\), \(x \to −\infty\) としても成り立つ。
指数関数の極限
指数関数の指数が無限大に向かうとき、極限値は次のようになります。
指数関数 \(y = a^x\) について
- \(1 < a\) のとき
\(\displaystyle \lim_{x \to \infty} a^x = \infty\)
\(\displaystyle \lim_{x \to −\infty} a^x = 0\) - \(0 < a < 1\) のとき
\(\displaystyle \lim_{x \to \infty} a^x = 0\)
\(\displaystyle \lim_{x \to −\infty} a^x = \infty\)
対数関数の極限
対数関数の真数が無限大や \(0\) に向かうとき、極限値は次のようになります。
対数関数 \(y = \log_a x\) について
- \(1 < a\) のとき
\(\displaystyle \lim_{x \to \infty} \log_a x = \infty\)
\(\displaystyle \lim_{x \to +0} \log_a x = −\infty\) - \(0 < a < 1\) のとき
\(\displaystyle \lim_{x \to \infty} \log_a x = −\infty\)
\(\displaystyle \lim_{x \to +0} \log_a x = \infty\)
ネイピア数 \(e\) の定義と関連公式
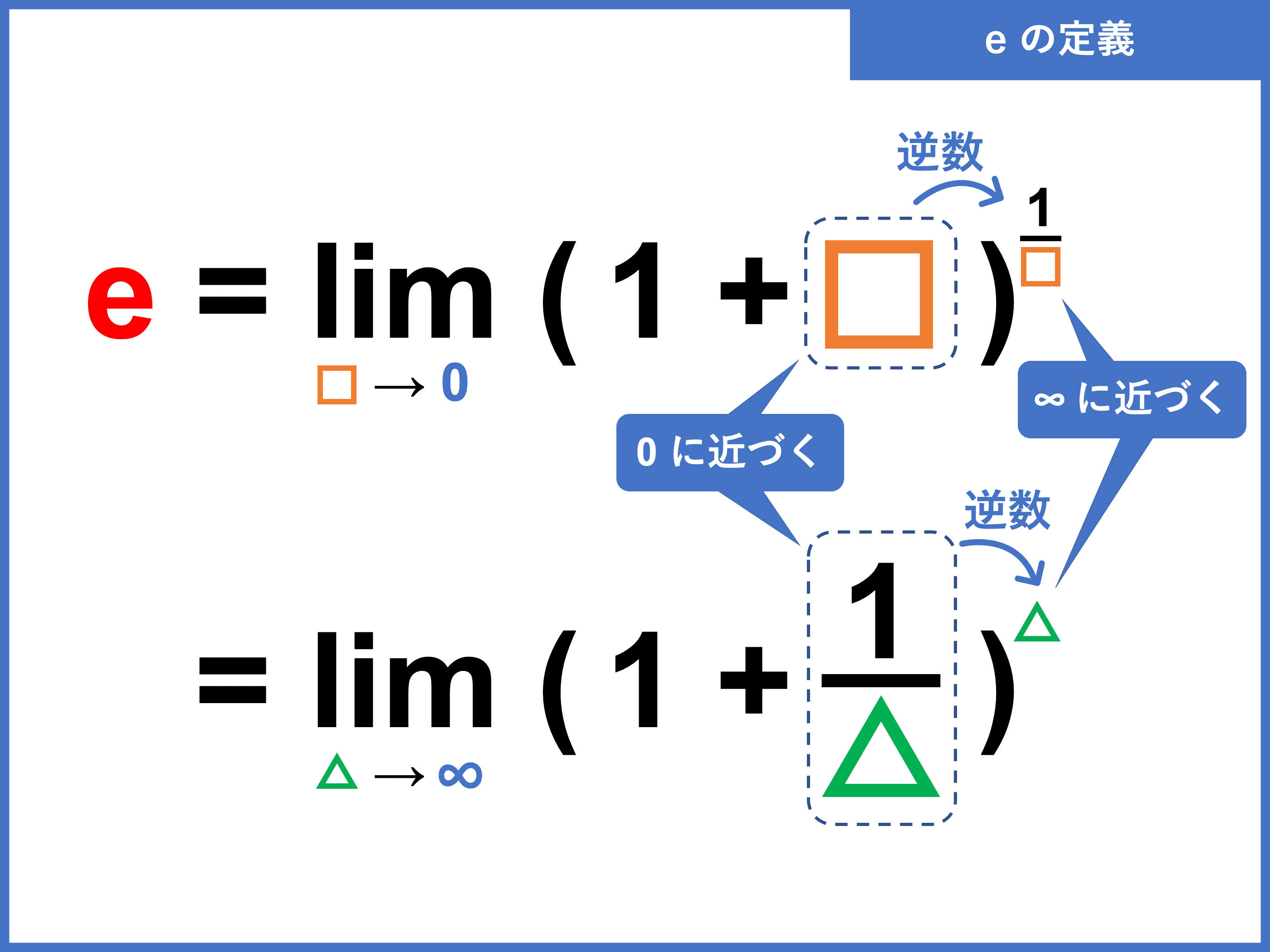
自然対数の底 \(e\) (ネイピア数)は、次の極限で定義されます。
\begin{align} e &= \lim_{h \to 0} (1 + h)^{\frac{1}{h}} \\ &= \lim_{n \to \pm\infty} \left( 1 + \frac{1}{n} \right)^n \\ &= 2.71828\cdots \end{align}
この定義式を利用して極限を求める問題もあるので、必ず覚えておきましょう。
その際、\(h\) や \(n\) の部分には別の文字を使うこともあるので、位置関係で覚えておきましょう。
「ネイピア数」については、以下の記事でより詳しく説明しています。
 自然対数 ln、自然対数の底 e とは?定義や微分積分公式
自然対数 ln、自然対数の底 e とは?定義や微分積分公式
また、\(e\) の定義に関連して以下の指数関数・対数関数の極限の公式も成り立ちます。
- \(\displaystyle \lim_{x \to 0} \frac{e^x − 1}{x} = 1\)
- \(\displaystyle \lim_{x \to 0} \frac{x}{\log(1 + x)} = 1\)
難関大の入試などでは割と普通に出てくるので把握しておいた方がよいでしょう。
三角関数の極限
三角関数については、以下の極限公式を覚えておきましょう。
- \(\displaystyle \lim_{x \to 0} \frac{\sin x}{x} = 1\)
- \(\displaystyle \lim_{x \to 0} \frac{x}{\sin x} = 1\)
- \(\displaystyle \lim_{x \to 0} \frac{\tan x}{x} = 1\)
(ただし、角 \(x\) の単位は弧度法)
関数の大小関係と極限
数列と同様、関数の大小関係から極限の大小関係を求められることがあります。
はさみうちの原理は絶対に押さえておきましょう!
\(\displaystyle \lim_{x \to a} f(x) = \alpha\), \(\displaystyle \lim_{x \to a} g(x) = \beta\) とすると、以下が成り立つ。
- \(x\) が \(a\) に近いとき、常に \(f(x) \leq g(x)\) ならば \(\alpha \leq \beta\)
- \(x\) が \(a\) に近いとき、常に \(f(x) \leq h(x) \leq g(x)\) かつ \(\alpha = \beta\) ならば \(\displaystyle \lim_{x \to a} h(x) = \alpha\)
(はさみうちの原理)
極限計算のポイント【例題】
最後に、いろいろな関数が含まれた極限の問題を解くときに知っておくべきポイントを説明します。
指数関数の極限の求め方
指数関数の問題は、指数の正負と底の大きさを必ず確認し、柔軟に対応しましょう。
次の極限を求めよ。
\(\displaystyle \lim_{x \to −\infty} \frac{4^x}{3^x + 2^x}\)
\(x \to −\infty\) のとき、底 \(a > 1\) なら \(a^x \to 0\)、底 \(0 < a < 1\) なら \(a^x \to \infty\) になります。
この問題は分数式なので、分母の項に着目します。
できるだけ値が収束する方向にもっていきたいので、分母にある \(2^x\) で分母・分子を割れば指数関数の底は \(a > 1\) のまま、うまく式変形できますね。
\(\displaystyle \lim_{x \to −\infty} \frac{4^x}{3^x + 2^x}\)
\(\displaystyle = \lim_{x \to −\infty} \frac{2^x}{\left( \frac{3}{2} \right)^x + 1}\)
\(\displaystyle = \frac{0}{0 + 1}\)
\(= 0\)
答え: \(\color{red}{0}\)
対数関数の極限の求め方
対数関数の極限を求める問題では、まず対数の項を \(1\) つにまとめましょう。
そのあと、真数部分の極限を考えます。
次の極限値を求めよ。
\(\displaystyle \lim_{x \to \infty} \left\{ \frac{1}{2} \log_3 x + \log_3 (\sqrt{3x + 1} − \sqrt{3x − 1}) \right\}\)
(見切れる場合は横へスクロール)
対数の性質「\(\log_a M + \log_a N = \log_a MN\)」を利用して、\(\log\) を \(1\) つにまとめます。
式変形の途中、無理式の部分は積よりも商(分数)にした方が扱いやすいので有理化しましょう。
(見切れる場合は横へスクロール)
\(\displaystyle \frac{1}{2} \log_3 x + \log_3 (\sqrt{3x + 1} − \sqrt{3x − 1})\)
\(\displaystyle = \log_3 \sqrt{x} + \log_3 \frac{(3x + 1) − (3x − 1)}{\sqrt{3x + 1} + \sqrt{3x − 1}}\)
\(\displaystyle = \log_3 \sqrt{x} + \log_3 \frac{2}{\sqrt{3x + 1} + \sqrt{3x − 1}}\)
\(\displaystyle = \log_3 \frac{2\sqrt{x}}{\sqrt{3x + 1} + \sqrt{3x − 1}}\)
より、
\(\displaystyle \lim_{x \to \infty} \left\{ \frac{1}{2} \log_3 x + \log_3 (\sqrt{3x + 1} − \sqrt{3x − 1}) \right\}\)
\(\displaystyle = \lim_{x \to \infty} \log_3 \frac{2\sqrt{x}}{\sqrt{3x + 1} + \sqrt{3x − 1}}\)
\(\displaystyle = \lim_{x \to \infty} \log_3 \frac{2}{\sqrt{3 + \frac{1}{x}} + \sqrt{3 − \frac{1}{x}}}\)
\(\displaystyle = \log_3 \frac{2}{2\sqrt{3}}\)
\(\displaystyle = \log_3 \frac{1}{\sqrt{3}}\)
\(\displaystyle = \log_3 3^{−\frac{1}{2}}\)
\(\displaystyle = −\frac{1}{2}\)
答え: \(\displaystyle \color{red}{−\frac{1}{2}}\)
三角関数の極限の求め方
三角関数は周期関数なので、単体では振動します。
(例)\(\displaystyle \lim_{n \to \infty} \cos n\pi\)
数列 \(\{\cos n\pi\}\) は \(−1, 1, −1, 1, −1, \cdots\)
と一定の値に収束せず、振動する。
よって極限はない。
よって、三角関数を含む問題では、式変形して三角関数の極限公式を用いるか、はさみうちの原理を用います。
ここでは、極限公式を用いる例を見てみましょう。
次の極限を求めよ。
\(\displaystyle \lim_{x \to \frac{\pi}{2}} \frac{\cos x}{2x − \pi}\)
\(x\) の一次式と \(\cos x\) の商(分数)の形になっているので、\(\color{red}{\displaystyle \frac{\sin◯}{◯}}\) の形にできないか考えます。
この問題では、文字の置き換えと変角公式を用いるとうまくいきます。
\(\displaystyle x − \frac{\pi}{2} = t\) とおくと、
\(\displaystyle x \to \frac{\pi}{2}\) のとき \(t \to 0\)
また、
\(\begin{align} \cos x &= \cos \left( t + \frac{\pi}{2} \right) \\ &= −\sin t \end{align}\)
\(\displaystyle 2x − \pi = 2\left( x − \frac{\pi}{2} \right) = 2t\)
より、求める極限は
\(\displaystyle \lim_{x \to \frac{\pi}{2}} \frac{\cos x}{2x − \pi}\)
\(\displaystyle = \lim_{t \to 0} \frac{−\sin t}{2t}\)
\(\displaystyle = \lim_{t \to 0} \left( −\frac{1}{2} \right) \cdot \frac{\sin t}{t}\)
\(\displaystyle = −\frac{1}{2}\)
答え: \(\displaystyle \color{red}{−\frac{1}{2}}\)
「はさみうちの原理」を使う問題については、以下の記事で解説しています。
 はさみうちの原理とは?使い方やコツをわかりやすく解説!
はさみうちの原理とは?使い方やコツをわかりやすく解説!
片側極限の求め方
片側極限は、\(+0\) や \(−0\) を含めた状態で代入するように求めましょう。
分数関数など、ある程度グラフの形がイメージできていると極限がより考えやすくなります。
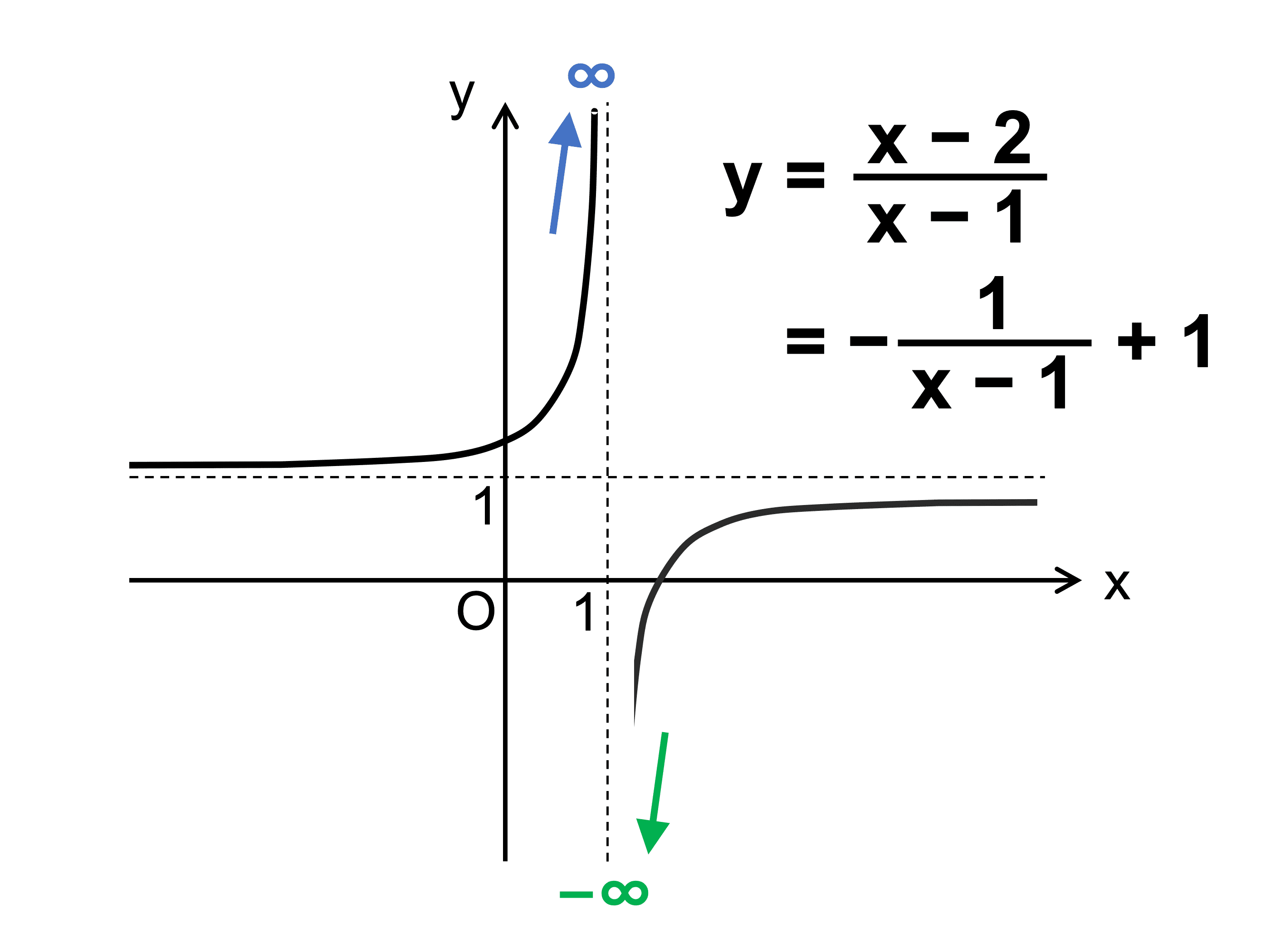
次の関数について、\(x\) が \(1\) に近づくときの右側極限、左側極限を求め、\(x \to 1\) のときの極限が存在するかを調べよ。
\(\displaystyle y = \frac{x − 2}{x − 1}\)
\(x \to 1 + 0\) のとき
\(x − 1 \to + 0\), \(x − 2 \to −1 + 0\)
よって \(\displaystyle \lim_{x \to 1 + 0} \frac{x − 2}{x − 1} = −\infty\)
また、\(x \to 1 − 0\) のとき
\(x − 1 \to −0\), \(x − 2 \to −1 − 0\)
よって \(\displaystyle \lim_{x \to 1 − 0} \frac{x − 2}{x − 1} = \infty\)
\(\displaystyle \lim_{x \to 1 + 0} \frac{x − 2}{x − 1} \neq \lim_{x \to 1 − 0} \frac{x − 2}{x − 1}\) より、
\(x \to 1\) のときの極限は存在しない。
答え: 極限なし
以上で問題も終わりです。
イメージするのが少し難しい極限ですが、微分積分や数列の分野などでもとても重要な概念です。
極限のコツをつかんで、ぜひマスターしてくださいね!
「不定形の極限」の解消法については、以下の記事で説明しています。
 不定形の極限の解消法!極限値の求め方を徹底解説
不定形の極限の解消法!極限値の求め方を徹底解説
