この記事では、「二項定理」についてわかりやすく解説します。
定理の証明や問題の解き方、分数を含むときの係数や定数項の求め方なども説明しますので、この記事を通してぜひマスターしてくださいね!
目次
二項定理とは?【公式】
二項定理とは、\((a + b)^n\) を展開した際の各項の係数を与える定理です。
\begin{align}&(a + b)^n \\&= {}_n\mathrm{C}_0 a^n + {}_n\mathrm{C}_1a^{n − 1}b + {}_n\mathrm{C}_2a^{n − 2}b^2 + \\& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdots + {}_n\mathrm{C}_r a^{n − r}b^r + \cdots + {}_n\mathrm{C}_n b^n\end{align}
一般項(第 \(r + 1\) 項):\(\color{red}{{}_n\mathrm{C}_r a^{n − r}b^r}\)
複雑な定理に見えますが、慣れてしまえばとても簡単で便利な定理です。
和を意味するシグマ \(\sum\) の記号を使うと、よりスッキリと表せます。
\begin{align}\color{red}{(a + b)^n = \sum_{k = 0}^n {}_n\mathrm{C}_k a^{n − k} b^k}\end{align}
 シグマ Σ とは?記号の意味や和の公式、証明や計算問題
シグマ Σ とは?記号の意味や和の公式、証明や計算問題
二項定理の考え方
二項定理において注目するのは、\(\color{red}{{}_n\mathrm{C}_r}\) の部分です。
因数分解の公式「\((a + b)^2 = a^2 + 2ab + b^2\)」を例に考えてみましょう(係数に注目するため、文字をあえて図形にします)。
\((◯ + △)^2 = ◯^2 + 2◯△ + △^2\)
左辺は、分配法則を使って右辺の形に展開したのでしたね。
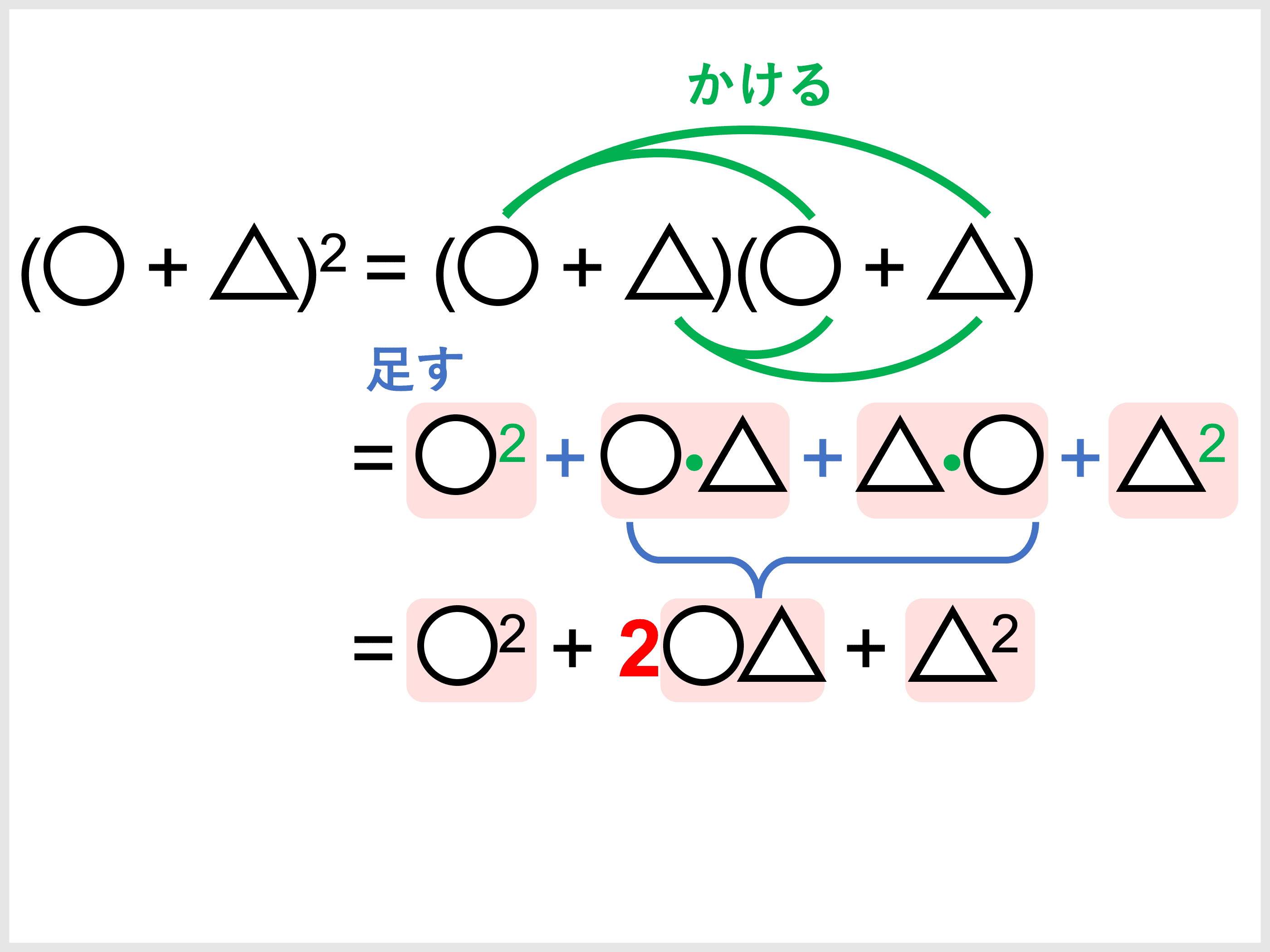
ここで考え方を少し変えると、展開後の項は「すべてのカッコ()の中から◯か△のどちらかを選び取ってかけ合わせたもの」と考えることもできます。
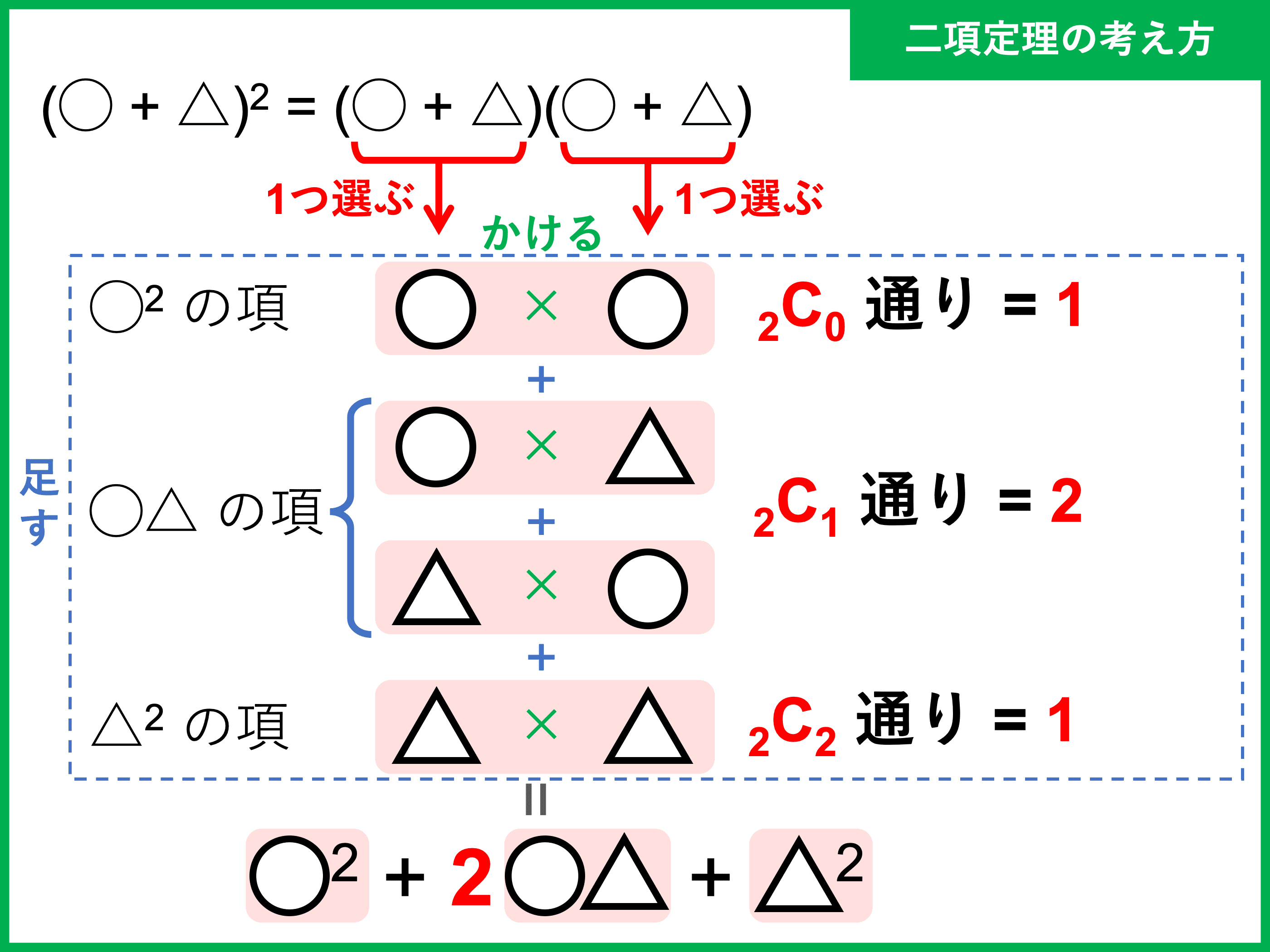
片方の文字に着目すると、「異なる \(2\) 個のカッコ()の中から△を \(0\) or \(1\) or \(2\) 個(または◯ を \(2\) or \(1\) or \(0\) 個)選んでかけ合わせる」ことになります。
だから、展開後の項の係数の部分は組み合わせの計算で求められるのです。
\((◯ + △)^2\)
\(= \color{red}{{}_2\mathrm{C}_0} ◯^2 + \ \color{red}{{}_2\mathrm{C}_1} ◯△ + \color{red}{{}_2\mathrm{C}_2} △^2\)
\(= ◯^2 + 2◯△ + △^2\)
これは、\(3\) 乗、\(4\) 乗…とべき乗の数を増やしても成り立ちます。
つまり、\((◯ + △)^n\) の展開は「異なる \(n\) 個のカッコ()の中から \(△\) を \(0\) ~ \(n\) 個選び、かけ合わせる」こと、これが二項定理なのです。
組み合わせ \(\bf{{}_n\mathrm{C}_r}\)
異なる \(n\) 個のものから異なる \(r\) 個を取り出す(選び出す)場合の数。
\begin{align} {}_n \mathrm{C}_r &= \frac{{}_n \mathrm{P}_r}{r!} \\&= \frac{n!}{r!(n − r)!} \\ &= \frac{n(n − 1)(n − 2) \cdots (n − r + 1)}{r(r − 1)(r − 2) \cdots 1}\end{align}
 組み合わせ C とは?公式や計算方法(◯◯は何通り?)
組み合わせ C とは?公式や計算方法(◯◯は何通り?)
二項定理の証明
ここでは、二項定理が成り立つことを数学的帰納法を使って証明します。
\(\displaystyle (a + b)^n = \sum_{k=0}^n {}_n\mathrm{C}_k a^{n−k} b^k\) …①
を数学的帰納法で示す。
(i) \(n = 1\) のとき
(左辺) \(= (a + b)^1 = a + b\)
(右辺) \(= {}_1\mathrm{C}_0 \cdot a^1 \cdot b^0 + {}_1\mathrm{C}_1 \cdot a^0 \cdot b^1 = a + b\)
より、①は成り立つ。
(ii) \(n = m\) のとき、①が成り立つと仮定すると、
\(\displaystyle (a + b)^m = \sum_{k=0}^m {}_m\mathrm{C}_k a^{m−k} b^k\) …②
\(n = m + 1\) のときを考えると、②より
\((a + b)^{m + 1}\)
\(= (a + b)^m \cdot (a + b)\)
\(\displaystyle = \sum_{k=0}^m {}_m\mathrm{C}_k a^{m − k} b^k \cdot (a + b)\)
\(\displaystyle = \sum_{k=0}^m {}_m\mathrm{C}_k (a^{m + 1 − k} b^k + a^{m − k} b^{k + 1})\)
\(a^{m + 1 − k}b^k\) の項だけ取り出すと、
(\(\sum\) 内第 \(2\) 項も \(k \to k − 1\) で \(a^{m + 1 − k}b^k\) の項が出ることに注意)
\(({}_m\mathrm{C}_k + {}_m\mathrm{C}_{k − 1}) a^{m + 1 − k}b^k\)
ここで
\({}_m\mathrm{C}_k + {}_m\mathrm{C}_{k − 1}\)
\(\displaystyle = \frac{m!}{(m − k)!k!} + \frac{m!}{(m − k + 1)!(k − 1)!}\)
\(\displaystyle = \frac{m!}{(m − k)!(k − 1)!} \cdot \left( \frac{1}{k} + \frac{1}{m − k + 1} \right)\)
\(\displaystyle = \frac{m!}{(m − k)!(k − 1)!} \cdot \frac{m + 1}{k(m − k + 1)}\)
\(\displaystyle = \frac{(m + 1)!}{(m +1 − k)!k!}\)
\(= {}_{m + 1}\mathrm{C}_k\)
より、
\(\displaystyle (a + b)^{m + 1} = \sum_{k=0}^{m+1} {}_{m + 1}\mathrm{C}_k a^{m + 1 − k}b^k\)
となり、\(n = m + 1\) のときも成り立つ。
(i)(ii)より、すべての自然数について二項定理①は成り立つ。
(証明終わり)
【発展】多項定理
また、項が \(2\) つ以上あっても成り立つ多項定理も紹介しておきます。
\((a_1 + a_2 + \cdots + a_m)^n\) の展開後の項 \(a_1^{k_1} a_2^{k_2} \cdots a_m^{k_m}\) の係数は、
\begin{align}\color{red}{\frac{n!}{k_1!k_2! \cdots k_m!}}\end{align}
ただし、
\(k_1 + k_2 + \cdots + k_m = n\)
任意の自然数 \(i\) \((i \leq m)\) について \(k_i \geq 0\)
高校では、三項 \((m = 3)\) の場合の式を扱うことがあります。
\((a + b + c)^n\) の一般項は
\begin{align}\color{red}{\displaystyle \frac{n!}{p!q!r!} a^p b^q c^r}\end{align}
ただし、
\(p + q + r = n\)
\(p \geq 0\), \(q \geq 0\), \(r \geq 0\)
例として、\(n = 2\) なら
\((a + b + c)^2\)
\(\displaystyle = \frac{2!}{2!0!0!} a^2 + \frac{2!}{0!2!0!} b^2 + \frac{2!}{0!0!2!} c^2 \) \(\displaystyle + \ \frac{2!}{1!1!0!} ab + \frac{2!}{0!1!1!} bc + \frac{2!}{1!0!1!} ca\)
\(\displaystyle = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
となります。
三項のべき乗は意外とよく登場するので、三項バージョンは覚えておいて損はないですよ!
ちなみに、多項定理は二項定理を前提とすると証明できます。
(\((a_1 + a_2 + \cdots + a_m)^n \) \( = \{(a_1 + a_2 + \cdots + a_{m − 1}) + a_m\}^n\)
などとし、二項の展開と見る)
二項定理による係数・定数項の求め方
二項定理を使うと、展開後の項の係数や、定数項を求められます。
例題を見ていきましょう。
例題①「係数を求める」
\((a + b)^5\) を展開したときの \(a^3 b^2\) の係数を求めよ。
\(5\) 乗を頑張って展開するのはあまりにも大変ですが、二項定理なら楽勝です。
二項定理より、\((a + b)^5\) の展開式の一般項は
\({}_5\mathrm{C}_r a^{5 − r} b^r\)
\(a^3 b^2\) の項は、\(r = 2\) のときであるから
\(a^3 b^2\) の係数は
\(\displaystyle {}_5\mathrm{C}_2 = \frac{5 \cdot 4}{2 \cdot 1} = 10\)
答え: \(\color{red}{10}\)
例題②「定数項を求める(分数を含む式)」
\(\displaystyle \left( x + \frac{2}{x} \right)^4\) を展開したときの定数項を求めよ。
分数を含む二項の展開です。
展開後に定数項となるのは、\(\displaystyle x^2 \left( \frac{2}{x} \right)^2\) の項ですね。
二項定理より、\(\displaystyle \left( x + \frac{2}{x} \right)^4\) の展開式の一般項は
\(\displaystyle {}_4\mathrm{C}_r x^{4 − r} \left( \frac{2}{x} \right)^r\)
定数項は、\(r = 2\) のときであるから
\(\begin{align} {}_4\mathrm{C}_2 x^2 \left( \frac{2}{x} \right)^2 &= \frac{4 \cdot 3}{2 \cdot 1} x^2 \cdot \frac{4}{x^2} \\ &= 24 \end{align}\)
答え: \(\color{red}{24}\)
例題③「定数項を求める(分数を含む式)」
\(\displaystyle \left( x^3 + \frac{1}{2x^2} \right)^5\) を展開したときの定数項を求めよ。
先ほどの例題より少しだけ複雑ですが、考え方は同じです。
定数項になるのは、\(x^3\) と \(\displaystyle \frac{1}{2x^2}\) を何個ずつ選び取った場合かを考えましょう。
二項定理より、\(\displaystyle \left( x^3 + \frac{1}{2x^2} \right)^5\) の展開式の一般項は
\(\displaystyle {}_5\mathrm{C}_r (x^3)^{5 − r} \cdot \left( \frac{1}{2x^2} \right)^r\)
\(\displaystyle = \frac{{}_5\mathrm{C}_r}{2^r} \cdot \frac{x^{15 − 3r}}{x^{2r}}\)
これが定数になるのは \(15 − 3r = 2r\) のとき、
すなわち \(r = 3\) のときであるから、
定数項は
\(\displaystyle \frac{{}_5\mathrm{C}_3}{2^3} = \frac{5 \cdot 4}{2 \cdot 1 \cdot 2^3} = \frac{5}{4}\)
答え: \(\color{red}{\displaystyle \frac{5}{4}}\)
【参考】パスカルの三角形
\((a + b)^n\) の展開で現れる係数 \({}_n\mathrm{C}_r\) の値を並べたものを「パスカルの三角形」といいます。
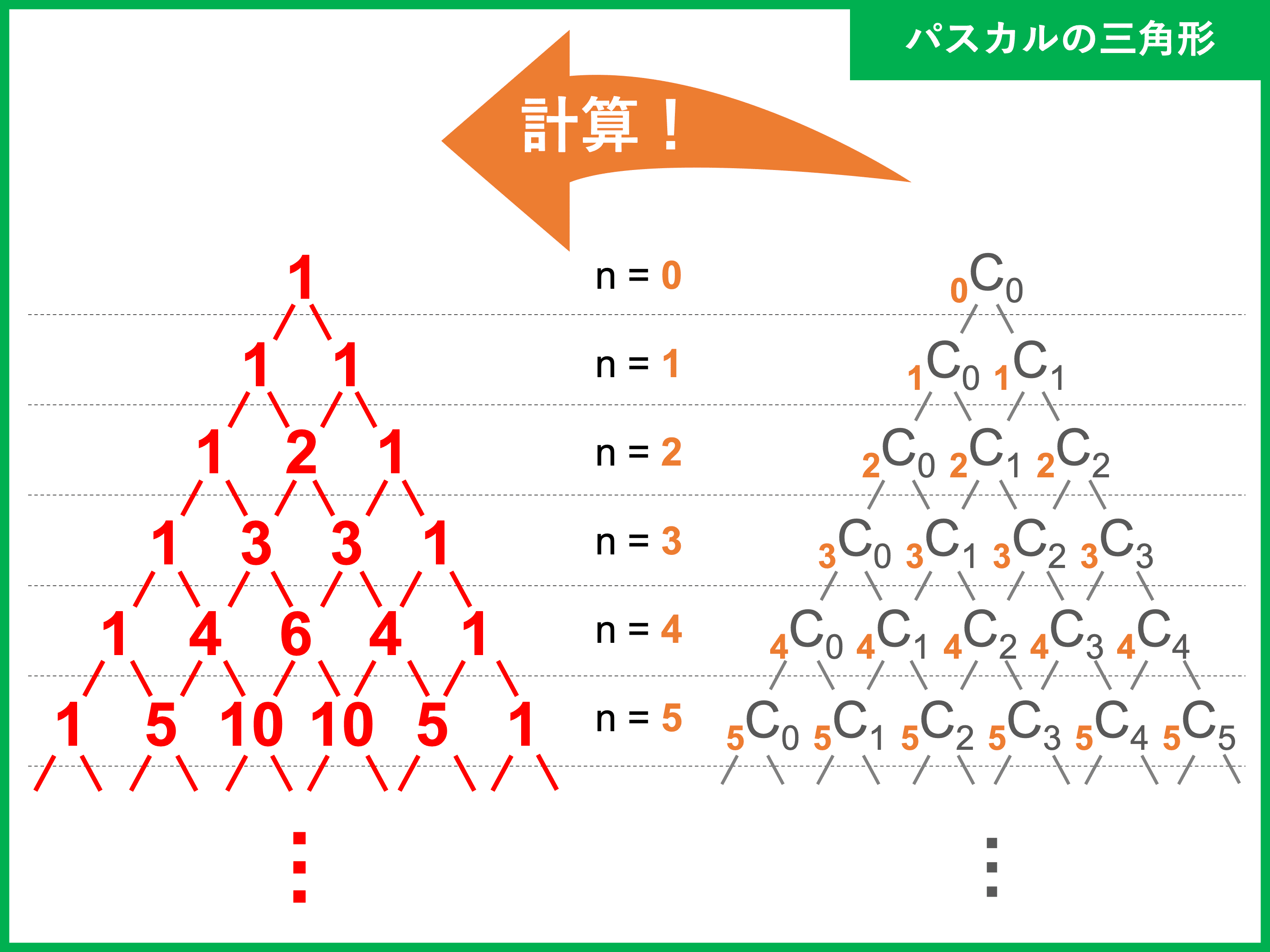
上から \(n\) 段目、左から \(r\) 番目の数字が \((a + b)^n\) を展開したときの \(a^r b^{n − r}\) の係数です。
それぞれの値は、斜め上の \(2\) 数を足したものになるという特徴があります。
(証明に登場した \({}_n\mathrm{C}_k + {}_n\mathrm{C}_{k − 1} = {}_{n + 1}\mathrm{C}_k\) と対応)
\(4\) 乗、\(5\) 乗の展開で手早く係数を求めたい!というときなどに利用してもよいですね。
二項定理の応用問題
最後に、二項定理を使う応用問題に挑戦してみましょう。
応用問題①「3 項の展開、係数を求める」
\((a + 2b + c)^6\) を展開したときの \(a^3 bc^2\) の係数を求めよ。

三項の場合の多項定理を使えば簡単です。
「多項定理は習っていない」「本番で思い出せない」という場合も、二項定理をうまく使うと解くことができますよ。
解答① 多項定理を利用
多項定理より、\(a^3 bc^2\) の項は
\(\begin{align} \frac{6!}{3!1!2!} \cdot a^3 (2b) c^2 &= 60 \cdot 2a^3 bc^2 \\ &= 120a^3 bc^2 \end{align}\)
よって、\(a^3 bc^2\) の係数は \(\color{red}{120}\)
解答② 二項定理を利用
二項定理より、
\(\{(a + 2b) + c\}^6\) の展開式において \(c^2\) を含む項は
\({}_6\mathrm{C}_2 (a + 2b)^4 c^2 = 15(a + 2b)^4 c^2\)
また、\((a + 2b)^4\) の展開式において \(a^3 b\) を含む項は
\({}_4\mathrm{C}_1 a^3 (2b)^1 = 8a^3 b\)
よって、\(a^3 bc^2\) の項は
\(15 \cdot 8a^3 bc^2 = 120a^3 bc^2\)
よって、\(a^3 bc^2\) の係数は \(\color{red}{120}\)
答え: \(\color{red}{120}\)
応用問題②「等式の証明問題」
\({}_n\mathrm{C}_0 + {}_n\mathrm{C}_1 + {}_n\mathrm{C}_2 + \cdots + {}_n\mathrm{C}_n = 2^n\) を示せ。

\({}_n\mathrm{C}_r\)(コンビネーション)がたくさん並んだ式の証明は、二項定理を使うと上手くいくことが多いです。
右辺を二項のべき乗にできないか、よく式を見てみましょう。
(見切れる場合は横へスクロール)
二項定理より、
\((x + 1)^n\)
\(= {}_n\mathrm{C}_0 \cdot x^n \cdot 1^0 + {}_n\mathrm{C}_1 \cdot x^{n−1} \cdot 1^1 \) \(+ \ {}_n\mathrm{C}_2 \cdot x^{n−2} \cdot 1^2 + \cdots + {}_n\mathrm{C}_n \cdot x^0 \cdot 1^n\)
\(= {}_n\mathrm{C}_0 x^n + {}_n\mathrm{C}_1 x^{n−1} + {}_n\mathrm{C}_2 x^{n−2} + \cdots + {}_n\mathrm{C}_n\) …①
①に \(x = 1\) を代入すると、
\(2^n = {}_n\mathrm{C}_0 + {}_n\mathrm{C}_1 + {}_n\mathrm{C}_2 + \cdots + {}_n\mathrm{C}_n\)
よって、
\({}_n\mathrm{C}_0 + {}_n\mathrm{C}_1 + {}_n\mathrm{C}_2 + \cdots + {}_n\mathrm{C}_n = 2^n\) が成り立つ。
(証明終わり)
以上で問題も終わりです。
一見複雑に見える二項定理ですが、多項式の展開においてとても役に立つ知識です。
しっかりと理解して、使いこなせるようになりましょう!


(1+2x-x^2)^10の展開式 の場合で、x^3の係数の求め方を教えてほしいです。
返信が遅くなってしまい申し訳ありません。
当サイトに記載のない問題についての質問には、原則回答を控えております。
学校や問題集等、信頼できるところから回答をお求めください。