この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。
各種公式や問題の解き方なども説明していくので、ぜひこの記事を通してマスターしてくださいね!
目次
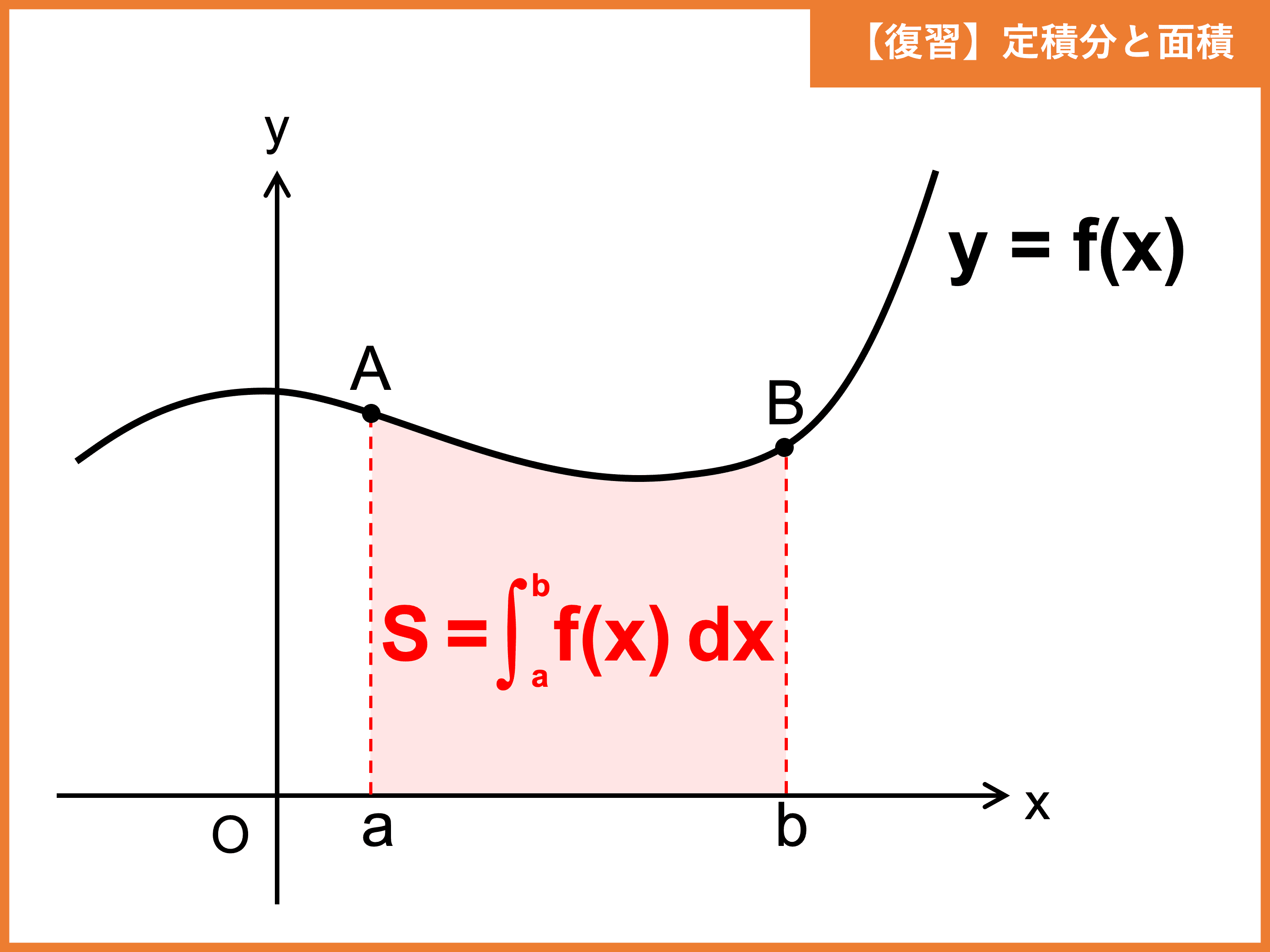
定積分で体積を求める
ある曲線下の面積を定積分で求められたように、ある平面を積み重ねてできる立体の体積も、定積分で求められます。
このとき、平面の積み重ね方には大きく分けて次の \(2\) 通りがあります。
- 平面を垂直に積み重ねる
- 平面を回転させる
例えば、円錐を例に考えてみましょう。
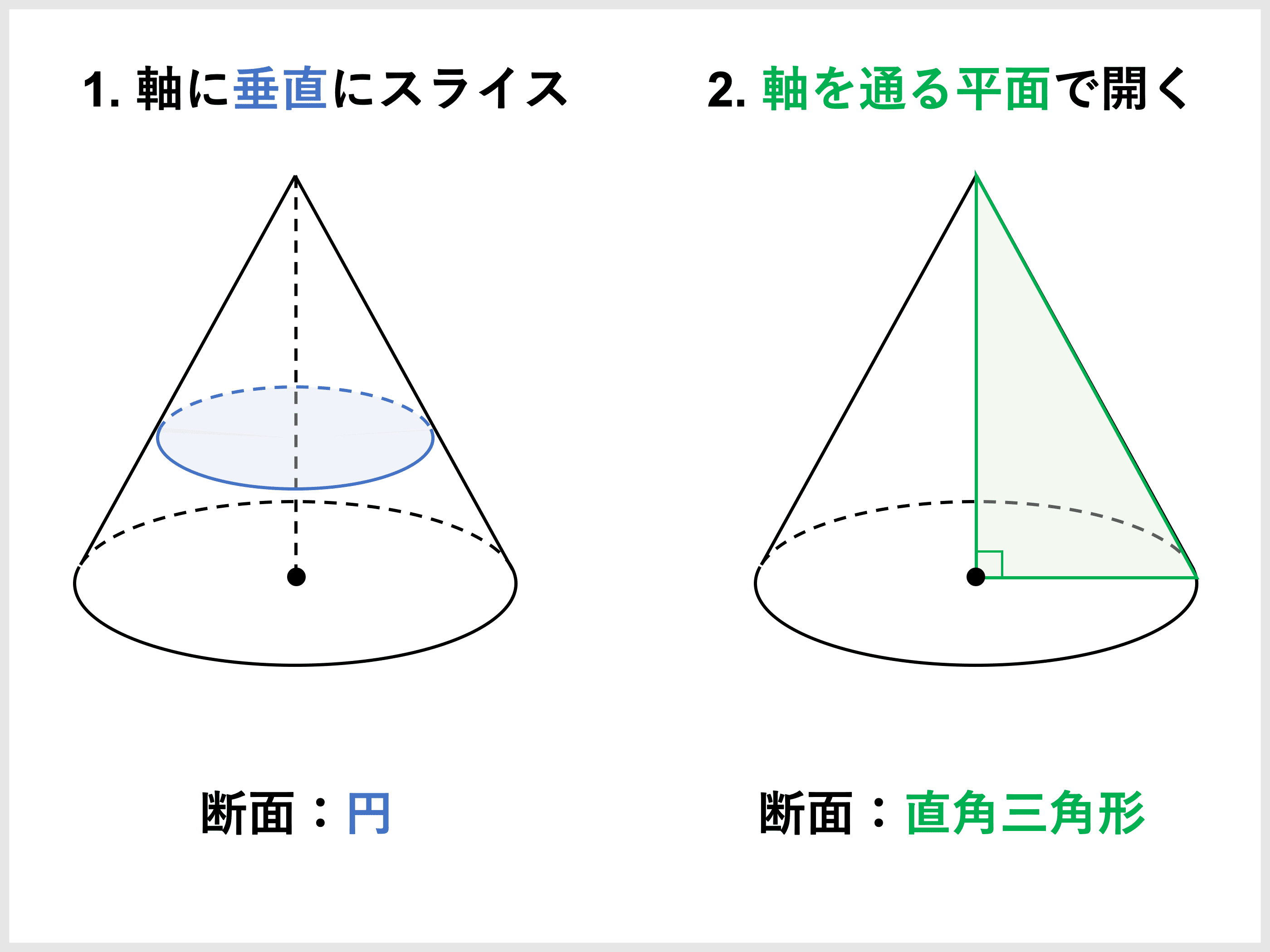
円錐を軸に対して垂直にスライスしてできる円を積み重ねていけば、体積が求められます。
また、軸を通る平面で開いてできた直角三角形を軸周りに回転しても、体積が求められますね。
積分計算の意味はまだ理解できなくてよいので、実際の計算を見てみましょう。
円錐の底面の半径を \(r\)、高さを \(h\)、求めたい体積を \(V\) とおく。

1. 垂直に積み重ね
円錐の頂点からの高さ \(x\) の位置で円錐をスライスしてできる円の断面積を \(S(x)\) とする。
円錐の底面積 \(S = \pi r^2\) であるから、
底面積と断面積の面積比は
\(S : S(x) = h^2 : x^2\)
よって
\(S(x) = \displaystyle \frac{x^2}{h^2}S\)
断面積 \(S(x)\) を高さ \(0\) から \(h\) まで積み重ねると
\(\begin{align}V &= \int_0^h S(x) \,dx \\&= \int_0^h \displaystyle \frac{x^2}{h^2}S \,dx \\&= \displaystyle \frac{S}{h^2} \left[\displaystyle \frac{x^3}{3} \right]_0^h \\&= \displaystyle \frac{S}{h^2} \cdot \frac{h^3}{3} \\&= \displaystyle \frac{1}{3} Sh \\&= \color{red}{\displaystyle \frac{1}{3}\pi r^2 h}\end{align}\)
2. 回転
円錐の軸を \(x\) 軸とおくと、母線が \(x\) 軸に対してなす傾きは \(\displaystyle \frac{r}{h}\)
\(f(x) = \displaystyle \frac{r}{h}x\) \((0 \leq x \leq h)\) を \(x\) 軸周りに回転させてできる立体の体積 \(V\) は
\(\begin{align}V &= \pi \int_0^h \left( \displaystyle \frac{r}{h}x \right)^2 \,dx \\&= \displaystyle \frac{\pi r^2}{h^2} \int_0^h x^2 \,dx \\&= \displaystyle \frac{\pi r^2}{h^2} \left[\frac{x^3}{3}\right]_0^h \\&= \displaystyle \frac{\pi r^2}{h^2} \cdot \frac{h^3}{3} \\&= \color{red}{\displaystyle \frac{1}{3}\pi r^2 h}\end{align}\)
どちらの方法でも、確かに円錐の体積は \(\color{red}{V = \displaystyle \frac{1}{3}\pi r^2 h}\) と求められました。
このように、ある立体の体積はその立体をなす平面の面積の積み重ね(または回転)で求められるのですね。
定積分と体積【公式】
まずは、平面を垂直に積み重ねて立体の体積を求める公式を確認しましょう。
\(x\) 軸に垂直な切り口の面積が \(S(x)\) である立体の、\(x = a\) から \(x = b\) \((a < b)\) における体積 \(V\) は
\begin{align} \color{red}{V = \int_a^b S(x) \,dx} \end{align}
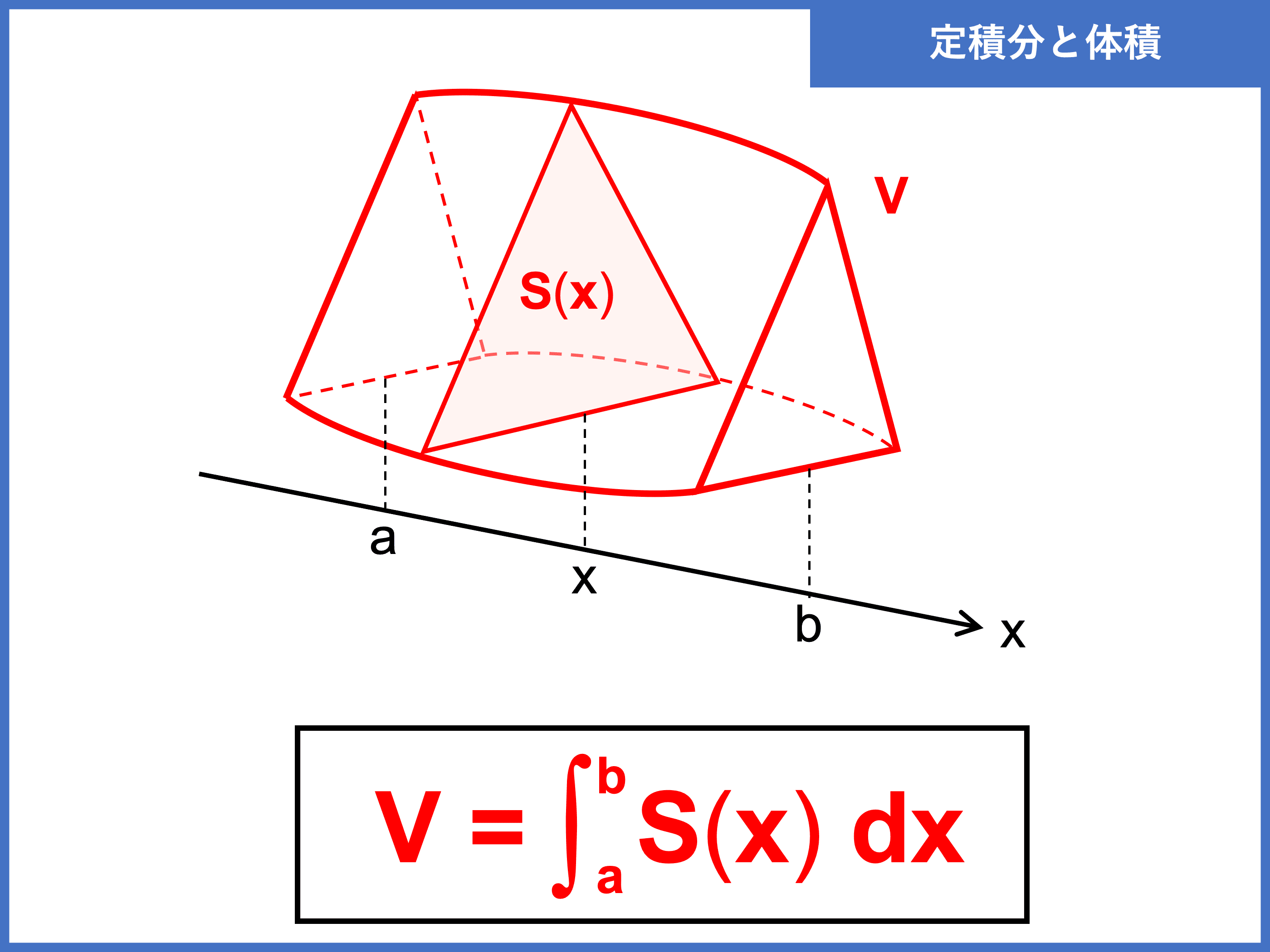
断面積の関数さえ特定できれば、それを定積分するだけですね。
例題「動く正三角形が描く立体の体積」
例題で公式の使い方を確認しましょう。
\(2\) 点 \(\mathrm{P}(x, 0)\)、\(\mathrm{Q}(x, \sin x)\) を結ぶ線分を \(1\) 辺とする正三角形を、\(x\) 軸に垂直な平面上に作る。
\(\mathrm{P}\) が \(x\) 軸上を原点 \(\mathrm{O}\) から点 \((\pi, 0)\) まで動くとき、この正三角形が描く立体の体積を求めよ。
まずは、簡単な図を書いて、体積を求めたい立体のイメージをつかみましょう。
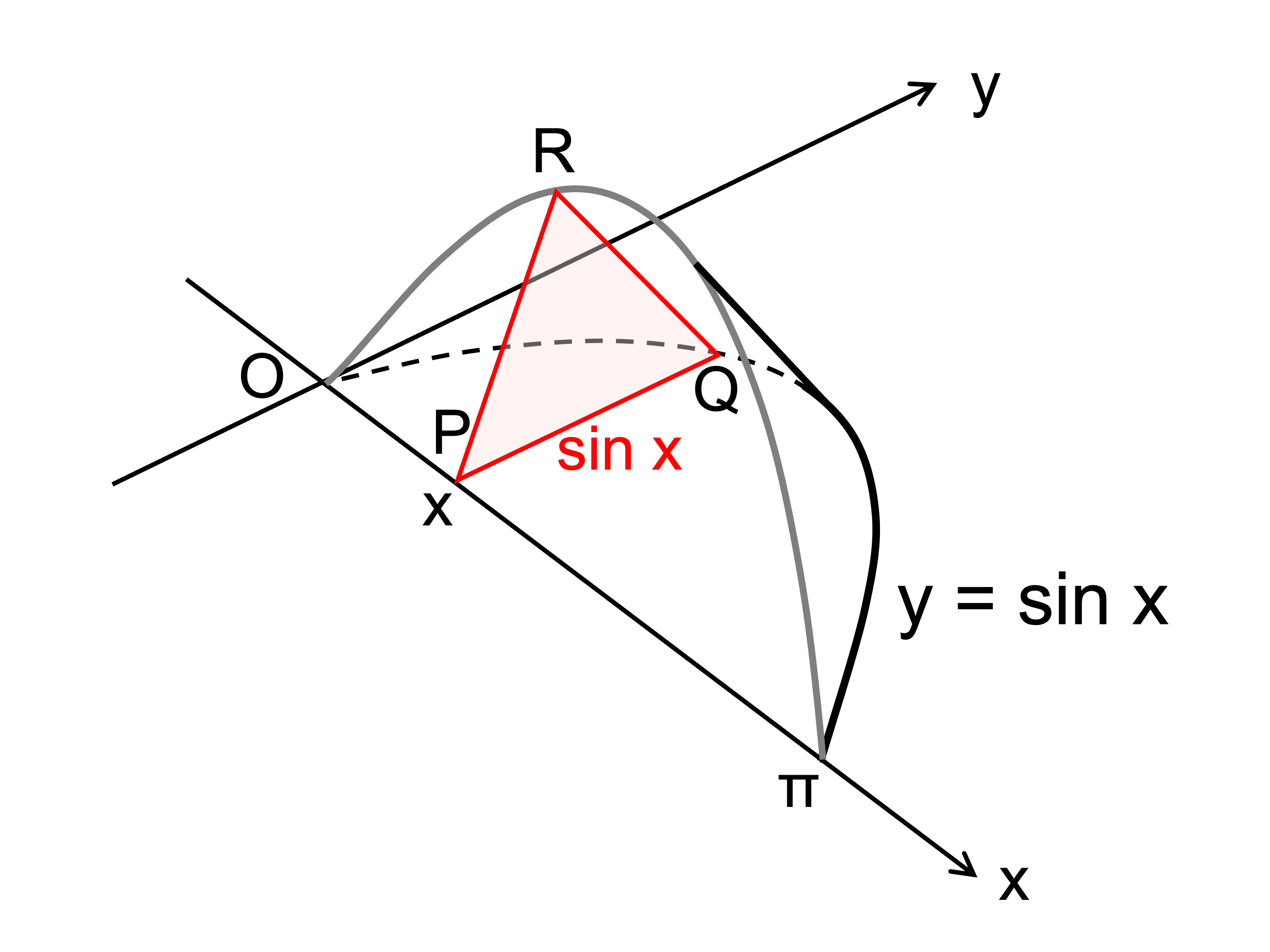
\(x\) 軸に垂直な平面でこの立体をスライスすれば、断面は必ず正三角形になりますね。
それでは、正三角形の面積を表す関数を求めましょう。
線分 \(\mathrm{PQ}\)(長さ \(\sin x\))を \(1\) 辺とする正三角形の面積を \(S(x)\) とおくと、
\(\begin{align} S(x) &= \displaystyle \frac{1}{2} \sin^2x \sin 60^\circ \\&= \displaystyle \frac{\sqrt{3}}{4} \sin^2x \end{align}\)
断面積がわかれば、あとは積み重ねて体積を求めるだけです。
よって求める立体の体積 \(V\) は
\(\begin{align} V &= \int_0^\pi S(x) \,dx \\&= \int_0^\pi \frac{\sqrt{3}}{4} \sin^2x \,dx \\&= \frac{\sqrt{3}}{8} \int_0^\pi (1 − \cos 2x) \,dx \\&= \frac{\sqrt{3}}{8} \left[x − \frac{1}{2}\sin 2x\right]_0^\pi \\&= \frac{\sqrt{3}}{8} {(\pi − 0) − (0 − 0)} \\&= \frac{\sqrt{3}}{8} \pi\end{align}\)
答え: \(\color{red}{\displaystyle \frac{\sqrt{3}}{8} \pi}\)
回転体の体積【公式】
次に、平面を回転させてできる立体の体積の公式を確認しましょう。
回転させる平面が \(x\) 軸に接している場合と、\(2\) つの曲線ではさまれている場合の \(2\) 通りがあります。
曲線 \(y = f(x)\) と \(x\) 軸と \(2\) 直線 \(x = a\), \(x = b\) \((a < b)\) で囲まれた部分を \(x\) 軸の周りに \(1\) 回転してできる回転体の体積 \(V\) は
\begin{align} \color{red}{V = \pi \int_a^b \{f(x)\}^2 dx = \pi \int_a^b y^2 \,dx} \end{align}

\(2\) つの曲線 \(y = f(x)\), \(y = g(x)\) (ただし \(f(x)\) と \(g(x)\) は同符号、すなわち \(f(x)g(x) \geq 0\))と \(2\) 直線 \(x = a\), \(x = b\) \((a < b)\) で囲まれた部分を \(x\) 軸の周りに \(1\) 回転してできる回転体の体積 \(V\) は
\begin{align} \color{red}{V = \pi \int_a^b |\{f(x)\}^2 − \{g(x)\}^2| \,dx} \end{align}

回転体の断面は必ず円となることから、どちらも円の面積を積分する計算になるのですね。
例題「曲線を x 軸周りに回転してできる立体の体積」
それぞれの公式を、例題で確認しましょう。
次の曲線や直線で囲まれた部分を \(x\) 軸の周りに \(1\) 回転させてできる立体の体積 \(V\) を求めよ。
(1) \(y = e^x\), \(x = 0\), \(x = 1\), \(x\) 軸
(2) \(y = −x^2 + 4x\), \(y = x\)
(1) から順番に解いていきます。
まずは状況をグラフに整理し、回転させる平面を確認します。
あとは、公式通りに回転体の体積を求めましょう。

よって、求める体積は
\(\begin{align} V &= \pi \int_0^1 (e^x)^2 \,dx \\&= \pi \left[\frac{1}{2} e^{2x}\right]_0^1 \\&= \frac{1}{2} (e^2 − 1)\pi \end{align}\)
答え: \(\color{red}{\displaystyle \frac{1}{2} (e^2 − 1)\pi}\)
続いて (2) です。
\(2\) つの曲線(または直線)ではさまれている場合は、まずそれらの交点を求めておきましょう。
\(−x^2 + 4x = x\) とおくと、
\(x^2 − 3x = 0\)
\(x(x − 3) = 0\)
\(x = 0, 3\)
よって \(y = −x^2 + 4x\) と \(y = x\) は点 \((0, 0)\)、\((3, 3)\) で交点をもつ。
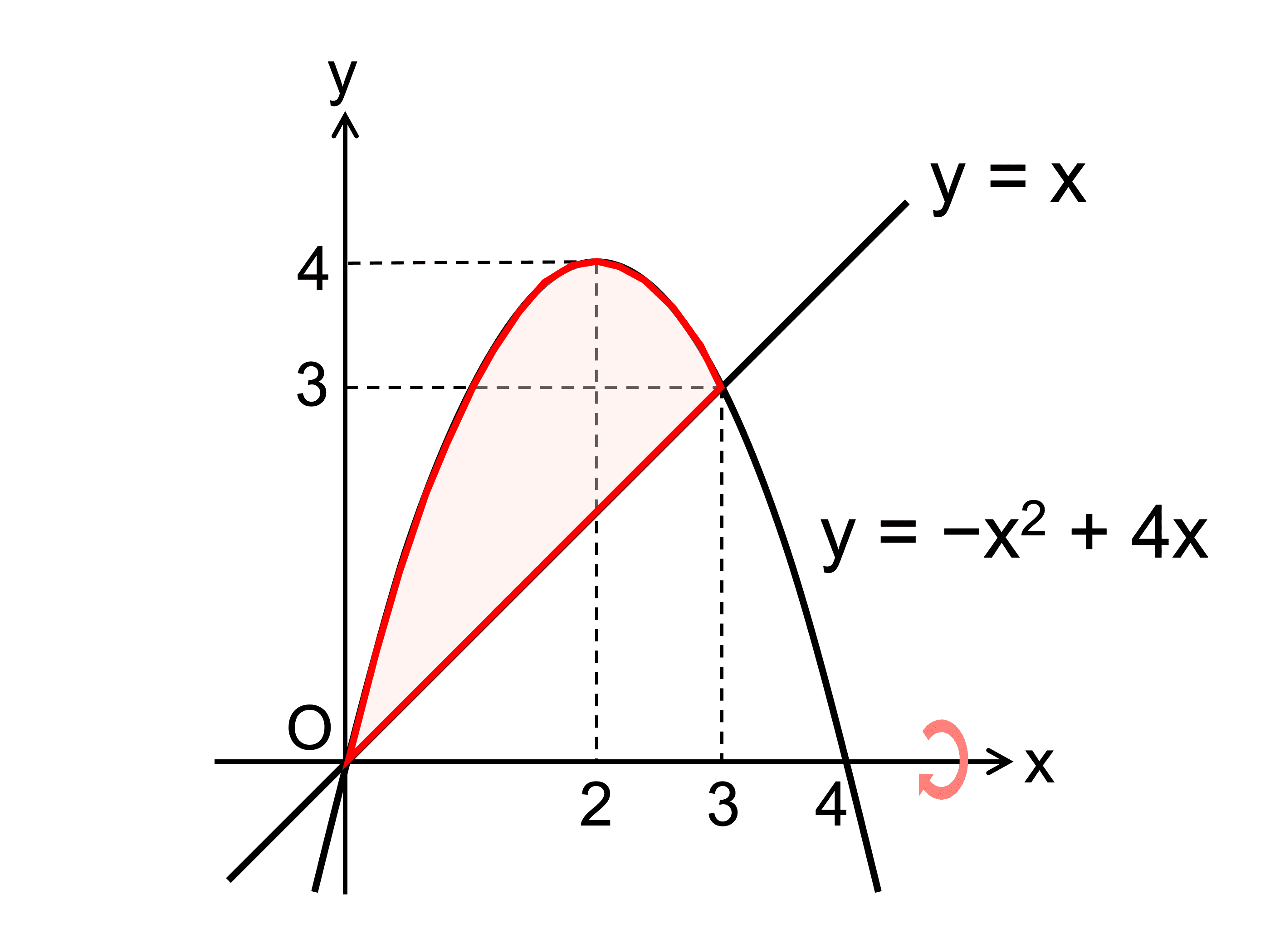
今度は断面がドーナツ状の円形になります。
つまり、大円の面積から小円の面積を引いたものが回転体の断面積ですね。
よって、求める体積は
\(\begin{align} V &= \pi \int_0^3 \{(−x^2 + 4x)^2 − x^2\} \,dx \\&= \pi \int_0^3 (x^4 − 8x^3 + 15x^2) \,dx \\&= \pi \left[\frac{x^5}{5} − 2x^4 + 5x^3 \right]_0^3 \\&= \pi \left(\frac{243}{5} − 162 + 135 \right) \\&= \frac{108}{5} \pi \end{align}\)
答え: \(\color{red}{\displaystyle \frac{108}{5} \pi}\)
積分と体積の計算問題
それでは最後に、積分で体積を求める計算問題に挑戦しましょう。
計算問題①「断面が二等辺三角形の体積」
半径 \(a\) の半円の直径を \(\mathrm{AB}\)、中心を \(\mathrm{O}\) とする。半円周上の点 \(\mathrm{P}\) から \(\mathrm{AB}\) に垂線 \(\mathrm{PQ}\) を引き、\(\mathrm{PQ}\) を底辺とし、高さが \(\mathrm{QO}\) の長さに等しい二等辺三角形 \(\mathrm{PQR}\) を半円と垂直な平面上に作り、\(\mathrm{P}\) を \(\stackrel{\frown}{\mathrm{AB}}\) 上で動かす。この \(\triangle{\mathrm{PQR}}\) が描く立体の体積 \(V\) を求めよ。

文章だと難しく思えがちですが、グラフを描いて状況がわかればなんてことはありません。
断面積、積分区間を調べたら、あとは体積の積分公式に当てはめるだけです。
半円を \(y = \sqrt{a^2 − x^2}\) とおき、\(\mathrm{Q}(x, 0)\) とする。
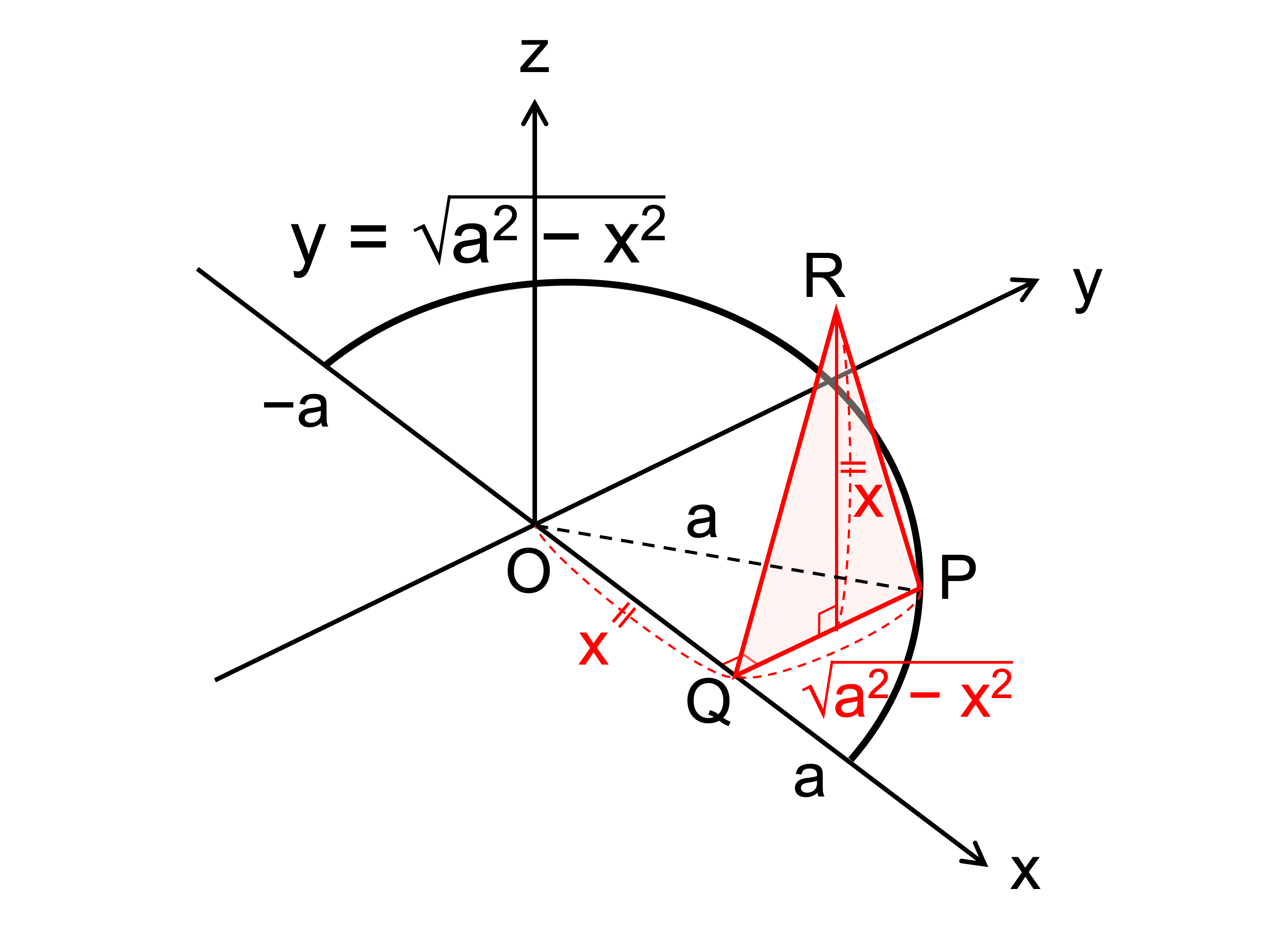
\(\triangle{\mathrm{PQR}}\) の面積を \(S(x)\) とすると、\(−a \leq x \leq a\) であり、
\(S(x) = \displaystyle \frac{1}{2} \mathrm{PQ} \cdot \mathrm{OQ} = \frac{1}{2}\sqrt{a^2 − x^2}|x|\)
このとき、\(S(−x) = S(x)\)、\(0 \leq x \leq a\) で \(|x| = x\) であるから、
\(\displaystyle V = \int_{−a}^a S(x) \ dx = \int_0^a \displaystyle x \sqrt{a^2 − x^2} \,dx \)
ここで、\(\sqrt{a^2 − x^2} = t\) とおくと、
\(a^2 − x^2 = t^2\), \(x \,dx = −t \,dt\)
| \(x\) | \(0 \rightarrow a\) |
| \(t\) | \(a \rightarrow 0\) |
よって、
\(\begin{align} V &= \int_0^a \displaystyle x \sqrt{a^2 − x^2} \ dx \\&= \int_a^0 t(−t) \,dt \\&= \int_0^a t^2 \,dt \\&= \left[\displaystyle \frac{t^3}{3}\right]_0^a \\&= \displaystyle \frac{a^3}{3} \end{align}\)
答え: \(\color{red}{\displaystyle \frac{a^3}{3}}\)
計算問題②「放物線と直線が囲む回転体の体積(x 軸周り)」
放物線 \(y = x^2 − 2x\) と直線 \(y = − x + 2\) で囲まれた部分を \(x\) 軸の周りに \(1\) 回転してできる立体の体積 \(V\) を求めよ。

曲線同士(または直線)で囲まれた部分が \(x\) 軸をまたぐ場合は、\(x\) 軸の下側にある部分を上側に折り返して考えます。
どの \(2\) つの曲線(または直線)で囲まれているのかに着目すると、\(3\) 区間に分けて積分できます。
\(x^2 − 2x = − x + 2\) とすると、
\(x^2 − x − 2 = 0\) より
\((x + 1)(x − 2) = 0\)
\(x = −1, 2\)
また、放物線を折り返した \(y = −x^2 + 2x\) と直線 \(y = −x + 2\) の交点の \(x\) 座標は
\(−x^2 + 2x = −x + 2\)
\(x^2 − 3x + 2 = 0\)
\((x − 1)(x − 2) = 0\)
\(x = 1, 2\)

求める回転体の体積は、上図の斜線部分を \(x\) 軸周りに \(1\) 回転すれば得られる。

よって
\(\begin{align}V &= (\text{回転体①}) + (\text{回転体②}) + (\text{回転体③}) \\\\&= \displaystyle \pi \int_{−1}^0 \{(−x + 2)^2 − (x^2 − 2x)^2\} \,dx + \pi \int_0^1 (−x + 2)^2 \,dx + \pi \int_1^2 (−x^2 + 2x)^2 \,dx \\\\&= \displaystyle \pi \int_{−1}^0 (−x^4 + 4x^3 − 3x^2 − 4x + 4) \,dx + \pi \int_0^1 (x − 2)^2 \,dx + \pi \int_1^2 (x^4 − 4x^3 + 4x^2)^2 \,dx \\\\&= \displaystyle \pi \left[ −\displaystyle \frac{x^5}{5} + x^4 − x^3 − 2x^2 + 4x \right]_{−1}^0 + \pi \left[ \displaystyle \frac{(x − 2)^3}{3} \right]_0^1 + \pi \left[ \displaystyle \frac{x^5}{5} − 4x^4 + \displaystyle \frac{4}{3}x^3 \right]_1^2 \\\\&= \displaystyle \frac{19}{5} \pi + \frac{7}{3} \pi + \frac{8}{15} \pi \\\\&= \displaystyle \frac{57 + 35 + 8}{15} \pi \\\\&= \displaystyle \frac{100}{15} \pi \\\\&= \displaystyle \frac{20}{3} \pi\end{align}\)
(見切れる場合は横へスクロール)
答え: \(\color{red}{\displaystyle \frac{20}{3} \pi}\)
計算問題③「対数関数が囲む回転体の体積(y 軸周り)」
曲線 \(y = \log(x^2 + 1)\) \((0 \leq x \leq 1)\) と直線 \(y = \log 2\)、および \(y\) 軸で囲まれた部分を \(y\) 軸の周りに \(1\) 回転してできる回転体の体積 \(V\) を求めよ。

\(y\) 軸周りの回転であることに注意です。
この場合、\(y\) の関数を \(y\) について積分すればよいですね。
\(\bf{y}\) 軸周りの回転
\(y = f(x) \iff x = g(y)\) のとき、
\begin{align}\color{red}{\displaystyle V = \pi \int_c^d \{g(y)\}^2 \,dy = \pi \int_c^d x^2 \,dy}\end{align}
\((c < d)\)
\(y = \log(x^2 + 1)\) から
\(x^2 + 1 = e^y\) すなわち \(x^2 = e^y − 1\)
また、\(0 \leq x \leq 1 \iff 0 \leq y \leq \log 2 \)

よって
\(\begin{align} V &= \pi \int_0^{\log 2} x^2 \,dy \\&= \pi \int_0^{\log 2} (e^y − 1) \,dy \\&= \pi [e^y − y]_0^{\log 2} \\&= \pi(2 − \log 2 − 1) \\&= \pi(1 − \log 2) \end{align}\)
答え: \(\color{red}{\pi(1 − \log 2)}\)
以上で問題も終わりです!
問題文を見ると「うっ、難しそう…」と感じる積分と体積ですが、求める立体の形がイメージできれば公式もすんなり思い浮かぶはずです。
積分計算でつまずく場合は、まず定積分についてしっかり復習しておきましょう!