この記事では、「中点連結定理」の意味や証明、定理の逆についてわかりやすく解説していきます。
また、問題の解き方もていねいに解説していくので、ぜひこの記事を通してマスターしてくださいね!
目次
中点連結定理とは?
中点連結定理とは、三角形の \(2\) 辺の中点を結んだ線分について成り立つ定理です。
\(\triangle \mathrm{ABC}\) の \(\mathrm{AB}\)、\(\mathrm{AC}\) の中点をそれぞれ \(\mathrm{M}\)、\(\mathrm{N}\) とすると、
\begin{align}\color{red}{\mathrm{MN} \ // \ \mathrm{BC}、\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}}\end{align}

三角形の \(2\) 辺の中点を結んだ線分は残りの \(1\) 辺と平行で、長さはその半分となります。
実は、よく見てみると \(\triangle \mathrm{AMN}\) と \(\triangle \mathrm{ABC}\) は相似比が \(1 : 2\) の相似な図形となっています。
そのことをあわせて理解しておくと、定理を忘れてしまっても思い出せますよ!
中点連結定理の使い方【例題】
例題で中点連結定理の使い方を確認しましょう。
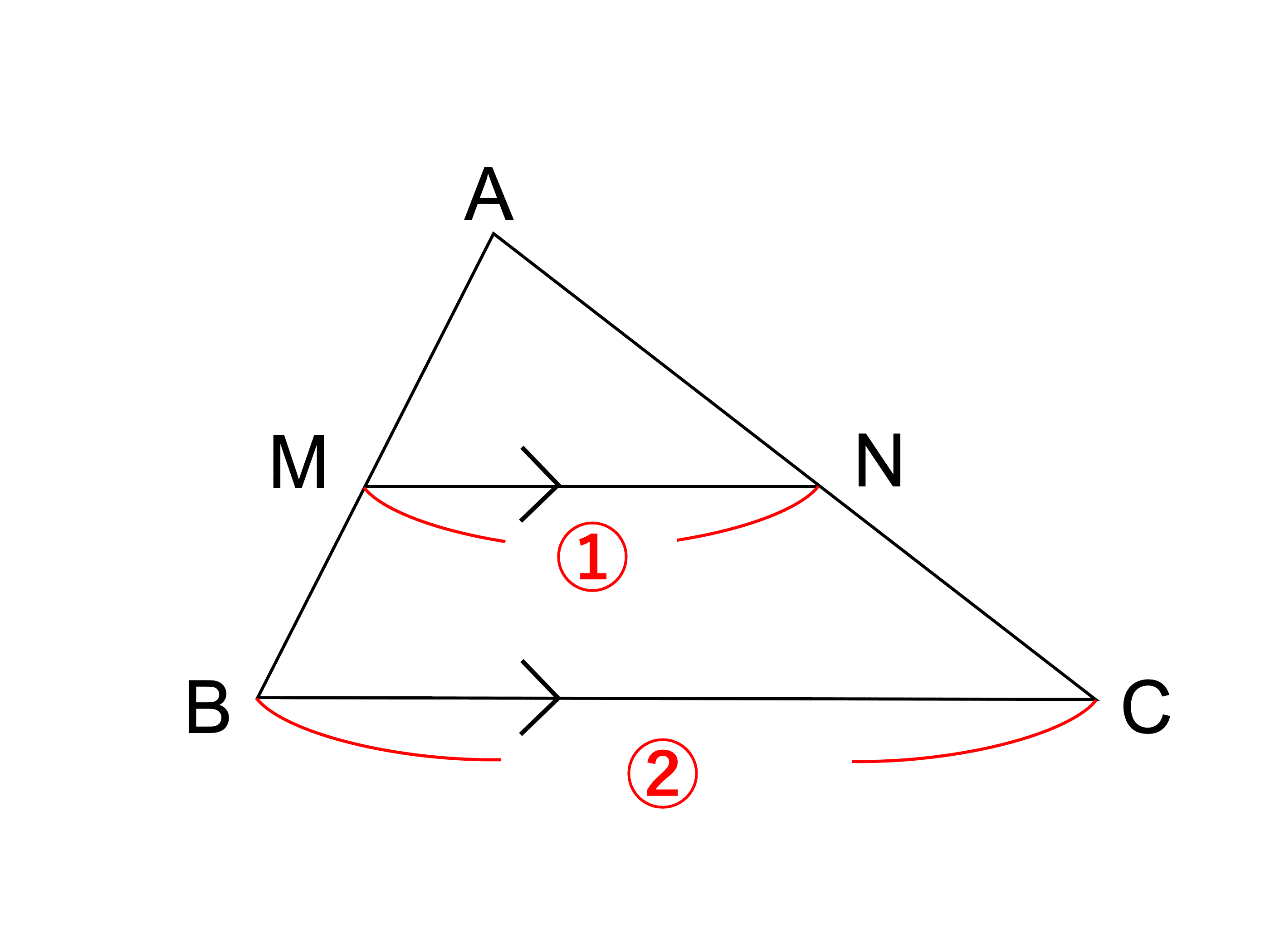
図の \(\triangle \mathrm{ABC}\) において、点 \(\mathrm{M}\)、\(\mathrm{N}\) はそれぞれ辺 \(\mathrm{AB}\)、\(\mathrm{AC}\) の中点である。
このとき、\(\mathrm{MN}\) の長さと \(\angle \mathrm{ABC}\) の大きさを求めなさい。

中点 \(\mathrm{M}\)、\(\mathrm{N}\) を結ぶ線分において、中点連結定理を用います。
中点連結定理より、
\(\begin{align} \mathrm{MN} &= \frac{1}{2} \mathrm{BC} \\ &= \frac{1}{2} \cdot 14 \\ &= 7 \end{align}\)
\(\mathrm{MN} \ // \ \mathrm{BC}\)
同位角は等しいので、
\(\angle \mathrm{ABC} = \angle \mathrm{AMN} = 45^\circ\)
答え: \(\color{red}{\mathrm{MN} = 7}\)、\(\color{red}{\angle \mathrm{ABC} = 45^\circ}\)
中点連結定理の証明
中点連結定理の証明について説明します。
\(\triangle \mathrm{ABC}\) の \(\mathrm{AB}\)、\(\mathrm{AC}\) の中点をそれぞれ \(\mathrm{M}\)、\(\mathrm{N}\) とするとき、
\begin{align}\mathrm{MN} \ // \ \mathrm{BC}、\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\end{align}
が成り立つことを示せ。
ここでは、\(2\) 通りの方法(三角形の相似を利用、平行四辺形の性質を利用)を示します。
中点連結定理の証明は問題として出ることもあるので、一通りの流れは把握しておきましょう!
証明① 三角形の相似を利用
\(\triangle \mathrm{AMN}\) と \(\triangle \mathrm{ABC}\) が相似であることを示し、対応する辺 \(\mathrm{MN}\)、\( \mathrm{BC}\) の関係を示します。
\(\triangle \mathrm{AMN}\) と \(\triangle \mathrm{ABC}\) において、 点 \(\mathrm{M}\)、\(\mathrm{N}\) はそれぞれ、辺 \(\mathrm{AB}\)、\(\mathrm{AC}\) の中点なので、 \(\mathrm{AM} : \mathrm{AB} = 1 : 2\) …① \(\mathrm{AN} : \mathrm{AC} = 1 : 2\) …② \(\angle \mathrm{A}\) は共通なので、 \(\angle \mathrm{MAN} = \angle \mathrm{BAC}\) …③ ①、②、③より、 \(2\) 組の辺の比とその間の角がそれぞれ等しいので、 \(\triangle \mathrm{AMN}\) ∽ \(\triangle \mathrm{ABC}\) ①より、相似比は \(\triangle \mathrm{AMN} : \triangle \mathrm{ABC} = 1 : 2\) なので、 \(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) …④ また、相似な図形では対応する角は等しいので \(\angle \mathrm{AMN} = \angle \mathrm{ABC}\) さらに、同位角が等しいので \(\mathrm{MN} \ // \ \mathrm{BC}\) …⑤ ④、⑤より、中点連結定理が成り立つ。 (証明終わり) 平行四辺形の性質「\(2\) 本の対角線が中点で交わる」を利用して、三角形の \(1\) 辺を対角線にもつ平行四辺形を考えます。 その後、別の平行四辺形の存在を示すことで、中点連結定理を証明します。 \(\mathrm{MN}\) の延長上に、\(\mathrm{MN} = \mathrm{ND}\) となる点 \(\mathrm{D}\) をとる。 点 \(\mathrm{D}\)、点 \(\mathrm{A}\)、点 \(\mathrm{C}\) を結ぶ。 また、点 \(\mathrm{M}\) と点 \(\mathrm{C}\) も結ぶ。 四角形 \(\mathrm{AMCD}\) において、 \(\mathrm{AN} = \mathrm{NC}\)、\(\mathrm{MN} = \mathrm{ND}\) より、 対角線がそれぞれの中点で交わるので、 四角形 \(\mathrm{AMCD}\) は平行四辺形である。 よって、 \(\mathrm{AM} = \mathrm{DC}\)、\(\mathrm{AM} \ // \ \mathrm{DC}\) となる。 また、四角形 \(\mathrm{MBCD}\) において、\(\mathrm{AM} = \mathrm{MB}\) より \(\mathrm{MB} = \mathrm{DC}\)、\(\mathrm{MB} \ // \ \mathrm{DC}\) となり、向かい合う \(1\) 組の辺が平行かつ等しいので、 四角形 \(\mathrm{MBCD}\) も平行四辺形である。 よって、 \(\mathrm{MN} \ // \ \mathrm{BC}\) \(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) となり、中線連結定理が成り立つ。 (証明終わり) 中点連結定理は、その逆も成立します。 \(\mathrm{AB}\) 上の点 \(\mathrm{M}\) と、\(\mathrm{AC}\) 上の点 \(\mathrm{N}\) が \(\mathrm{MN} \ // \ \mathrm{BC}\)、\(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) ならば、 点 \(\mathrm{M}\)、\(\mathrm{N}\) はそれぞれ、\(\mathrm{AB}\)、\(\mathrm{AC}\) の中点となる。 「平行で長さが半分とくれば、中点だ!」と結びつけておきましょう。 中点連結定理の逆も、相似な三角形の性質を利用して証明できます。 図の \(\triangle \mathrm{AMN}\) と \(\triangle \mathrm{ABC}\) において、\(\mathrm{MN} \ // \ \mathrm{BC}\)、\(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) とする。 仮定 \(\mathrm{MN} \ // \ \mathrm{BC}\) より、平行線の同位角は等しいので、 \(\angle \mathrm{AMN} = \angle \mathrm{ABC}\) …① \(\angle \mathrm{ANM} = \angle \mathrm{ACB}\) …② ①、②より \(2\) つの角がそれぞれ等しいので、 \(\triangle \mathrm{AMN}\) ∽ \(\triangle \mathrm{ABC}\) また、仮定 \(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) より、 \(\mathrm{MN} : \mathrm{BC} = 1 : 2\) なので、相似比は、 \(\triangle \mathrm{AMN} : \triangle \mathrm{ABC} = 1 : 2\) よって、 \(\mathrm{AM} : \mathrm{AB} = 1 : 2\) となり、\(\mathrm{AM} = \mathrm{MB}\) なので、 点 \(\mathrm{M}\) は、\(\mathrm{AB}\) の中点となる。 …③ 同じく、\(\mathrm{AN} : \mathrm{AC} = 1 : 2\) となり、\(\mathrm{AN} = \mathrm{NC}\) なので、 点 \(\mathrm{N}\) は、\(\mathrm{AC}\) の中点となる。 …④ ③、④より、中点連結定理の逆が成り立つ。 (証明終わり) 三角形において成り立つ中点連結定理ですが、実は四角形にも応用できます。 ここでは、台形の中点連結定理と、一般的な四角形の中点連結定理を紹介します。 台形における中点連結定理は次のとおりです。 \(\mathrm{AD} \ // \ \mathrm{BC}\) である台形 \(\mathrm{ABCD}\) において、辺 \(\mathrm{AB}\)、\(\mathrm{DC}\) の中点をそれぞれ、点 \(\mathrm{E}\)、\(\mathrm{F}\) とするとき、 \begin{align}\color{red}{\displaystyle \mathrm{EF} = \frac{1}{2} (\mathrm{AD} + \mathrm{BC})}\end{align} 以下の例題で、台形の中点連結定理の証明を示します。 \(\mathrm{AD} \ // \ \mathrm{BC}\) である台形 \(\mathrm{ABCD}\) がある。 辺 \(\mathrm{AB}\)、\(\mathrm{DC}\) の中点をそれぞれ、点 \(\mathrm{E}\)、\(\mathrm{F}\) とするとき、\(\mathrm{EF}\) の長さを文字を使って表しなさい。 補助線を引いて三角形を作ると、簡単に示すことができます。 \(\mathrm{BC}\) の延長上と \(\mathrm{AF}\) の交点を点 \(\mathrm{G}\) とおく。 \(\triangle \mathrm{ADF}\) と \(\triangle \mathrm{GCF}\) において、 対頂角は等しいので \(\angle \mathrm{AFD} = \angle \mathrm{GFC}\) …① 仮定より、点 \(\mathrm{F}\) は \(\mathrm{DC}\) の中点であるから \(\mathrm{DF} = \mathrm{CF}\) …② 点 \(\mathrm{G}\) は \(\mathrm{BC}\) の延長線上の点なので \(\mathrm{AD} \ // \ \mathrm{CG}\) より、平行線の錯角は等しい。 \(\angle \mathrm{ADF} = \angle \mathrm{GCF}\) …③ ①、②、③より、 \(1\) つの辺とその両端の角がそれぞれ等しいので、 \(\triangle \mathrm{ADF} \equiv \triangle \mathrm{GCF}\) よって、合同な図形では対応する辺の長さは等しいので、 \(\mathrm{AF} = \mathrm{GF}\) \(\mathrm{AD} = \mathrm{GC}\) \(\triangle \mathrm{ABG}\) において、 先ほど導いた \(\mathrm{AF} = \mathrm{GF}\) より、点 \(\mathrm{F}\) は辺 \(\mathrm{AG}\) の中点である。 また、\(\mathrm{AD} = \mathrm{GC}\) と \(\mathrm{BG} = \mathrm{BC} + \mathrm{CG}\) より、 \(\mathrm{BG} = \mathrm{AD} + \mathrm{BC}\) …④ 点 \(\mathrm{E}\)、\(\mathrm{F}\) はそれぞれの辺の中点なので、中点連結定理より \(\displaystyle \mathrm{EF} = \frac{1}{2} \mathrm{BG}\) ④を代入すると、 \(\displaystyle \mathrm{EF} = \frac{1}{2} (\mathrm{AD} + \mathrm{BC})\) よって、台形の平行でない向かい合う \(2\) つの辺の中点を結んだ線分は、上底と下底を合わせた長さの半分である。 つまり、台形における中点連結定理として、 \(\displaystyle \mathrm{EF} = \frac{1}{2} (\mathrm{AD} + \mathrm{BC})\) が成り立つ。 (証明終わり) 次に、四角形における中点連結定理の応用です。 四角形の中点をすべて結ぶと、平行四辺形になるという性質があります。 四角形 \(\mathrm{ABCD}\) の \(4\) 辺 \(\mathrm{AB}\)、\(\mathrm{BC}\)、\(\mathrm{CD}\)、\(\mathrm{DA}\) の中点を \(\mathrm{E}\)、\(\mathrm{F}\)、\(\mathrm{G}\)、\(\mathrm{H}\) とすると、 四角形 \(\mathrm{EFGH}\) は平行四辺形となる。 例題を通してこの性質を証明してみましょう。 以下の四角形 \(\mathrm{ABCD}\) のそれぞれの辺の中点を点 \(\mathrm{E}\)、\(\mathrm{F}\)、\(\mathrm{G}\)、\(\mathrm{H}\) とする。 このとき、四角形 \(\mathrm{EFGH}\) が平行四辺形になることを示せ。 対角線を引き、\(2\) つの三角形に分けると中点連結定理を利用できますね。 対角線 \(\mathrm{AC}\) を引く。 \(\triangle \mathrm{ABC}\) において、点 \(\mathrm{E}\)、\(\mathrm{F}\) はそれぞれ辺 \(\mathrm{AB}\)、\(\mathrm{BC}\) の中点なので、中点連結定理より \(\mathrm{EF} \ // \ \mathrm{AC}\) …① \(\displaystyle \mathrm{EF} = \frac{1}{2} \mathrm{AC}\) …② \(\triangle \mathrm{ADC}\) において、点 \(\mathrm{G}\)、\(\mathrm{H}\) はそれぞれ辺 \(\mathrm{DC}\)、\(\mathrm{DA}\) の中点なので、中点連結定理より \(\mathrm{HG} \ // \ \mathrm{AC}\) …③ \(\displaystyle \mathrm{HG} = \frac{1}{2} \mathrm{AC}\) …④ ①、③より、 \(\mathrm{EF} \ // \ \mathrm{HG}\) ②、④より、 \(\mathrm{EF} = \mathrm{HG}\) よって、\(1\) 組の向かい合う辺が平行で長さが等しいので、四角形 \(\mathrm{EFGH}\) は平行四辺形である。 (証明終わり) 最後に中点連結定理のまとめとして、計算問題を解いていきましょう。 \(\triangle \mathrm{ABC}\) において、辺 \(\mathrm{BC}\)、\(\mathrm{CA}\)、\(\mathrm{AB}\) の中点をそれぞれ点 \(\mathrm{D}\)、\(\mathrm{E}\)、\(\mathrm{F}\) とする。 \(\mathrm{BC} = 10\)、\(\mathrm{CA} = 8\)、\(\mathrm{DE} = 3\) のとき、以下の問いに答えなさい。 (1) \(\mathrm{AB}\) の長さを求めよ。 (2) \(\mathrm{DF}\) の長さを求めよ。 (3) \(\mathrm{EF}\) の長さを求めよ。 どの辺の長さを求めるかによって、頂点ととらえる点の位置が変わります。 対応する辺を間違えないように中点連結定理を使いましょう。 (1) 頂点を点 \(\mathrm{C}\) とする。 点 \(\mathrm{D}\)、\(\mathrm{E}\) はそれぞれ辺 \(\mathrm{BC}\)、\(\mathrm{CA}\) の中点なので、中点連結定理より \(\mathrm{AB} = 2\mathrm{DE} = 2 \cdot 3 = 6\) 答え: \(6\) (2) 頂点を点 \(\mathrm{B}\) とする。 点 \(\mathrm{D}\)、\(\mathrm{F}\) はそれぞれ辺 \(\mathrm{BC}\)、\(\mathrm{AB}\) の中点なので、中点連結定理より \(\mathrm{DF} = \displaystyle \frac{1}{2} \mathrm{CA} = \frac{1}{2} \cdot 8 = 4\) 答え: \(4\) (3) 頂点を点 \(\mathrm{A}\) とする。 点 \(\mathrm{E}\)、\(\mathrm{F}\) はそれぞれ辺 \(\mathrm{CA}\)、\(\mathrm{AB}\) の中点なので、中点連結定理より \(\mathrm{EF} = \displaystyle \frac{1}{2} \mathrm{BC} = \frac{1}{2} \cdot 10 = 5\) 答え: \(5\) \(\mathrm{GJ} \ // \ \mathrm{HI}\) の台形 \(\mathrm{GHIJ}\) において、\(\mathrm{GJ} = 3\)、\(\mathrm{HI} = 5\)、辺 \(\mathrm{GH}\)、\(\mathrm{JI}\) の中点がそれぞれ点 \(\mathrm{K}\)、\(\mathrm{L}\) のとき、\(\mathrm{KL}\) の長さを求めなさい。 点 \(\mathrm{K}\)、\(\mathrm{L}\) は辺 \(\mathrm{GH}\)、\(\mathrm{JI}\) の中点となっています。台形における中点連結定理を利用しましょう。 台形 \(\mathrm{GHIJ}\) の上底を \(\mathrm{GJ}\)、下底を \(\mathrm{HI}\) とすると、点 \(\mathrm{K}\)、\(\mathrm{L}\) は辺 \(\mathrm{GH}\)、\(\mathrm{JI}\) の中点なので、台形における中点連結定理より \(\begin{align} \mathrm{KL} &= \frac{1}{2} (\mathrm{GJ} + \mathrm{HI}) \\ &= \frac{1}{2} (3 + 5) \\ &= 4 \end{align}\) 答え: \(4\) 四角形 \(\mathrm{ABCD}\) において、点 \(\mathrm{E}\)、\(\mathrm{F}\)、\(\mathrm{G}\)、\(\mathrm{H}\) は各辺の中点である。 このとき、点 \(\mathrm{E}\)、\(\mathrm{F}\)、\(\mathrm{G}\)、\(\mathrm{H}\) を結んでできた四角形 \(\mathrm{EFGH}\) が平行四辺形であることを証明しなさい。 内角の \(1\) つが \(180^\circ\) を超える凹四角形ですね。 この場合も、通常の四角形と証明手順はなんら変わりません。 対角線を引いて、\(2\) つの三角形に分けてから中点連結定理を利用しましょう。 対角線 \(\mathrm{AC}\) を引く。 \(\triangle \mathrm{ABC}\) において、点 \(\mathrm{E}\)、\(\mathrm{F}\) はそれぞれ辺 \(\mathrm{BA}\)、\(\mathrm{BC}\) の中点なので、中点連結定理より \(\mathrm{EF} \ // \ \mathrm{AC}\) …① \(\displaystyle \mathrm{EF} = \frac{1}{2} \mathrm{AC}\) …② また、\(\triangle \mathrm{ADC}\) において、点 \(\mathrm{G}\)、\(\mathrm{H}\) はそれぞれ辺 \(\mathrm{DC}\)、\(\mathrm{DA}\) の中点なので、中点連結定理より \(\mathrm{HG} \ // \ \mathrm{AC}\) …③ \(\displaystyle \mathrm{HG} = \frac{1}{2} \mathrm{AC}\) …④ ①、③より、 \(\mathrm{EF} \ // \ \mathrm{HG}\) …⑤ ②、④より、 \(\mathrm{EF} = \mathrm{HG}\) …⑥ よって、⑤、⑥より、 \(1\) 組の向かい合う辺が平行で長さが等しいので、四角形 \(\mathrm{EFGH}\) が平行四辺形である。 (証明終わり) 以上で問題も終わりです! 中点連結定理は、\(2\) つの相似な三角形の辺の比として図とともに覚えておくと定着しますよ! 証明問題でもよく使われる定理なので、しっかりと覚えておきましょう。
証明② 平行四辺形の性質を利用

中点連結定理の逆
中点連結定理の逆の証明
中点連結定理の応用
台形の中点連結定理
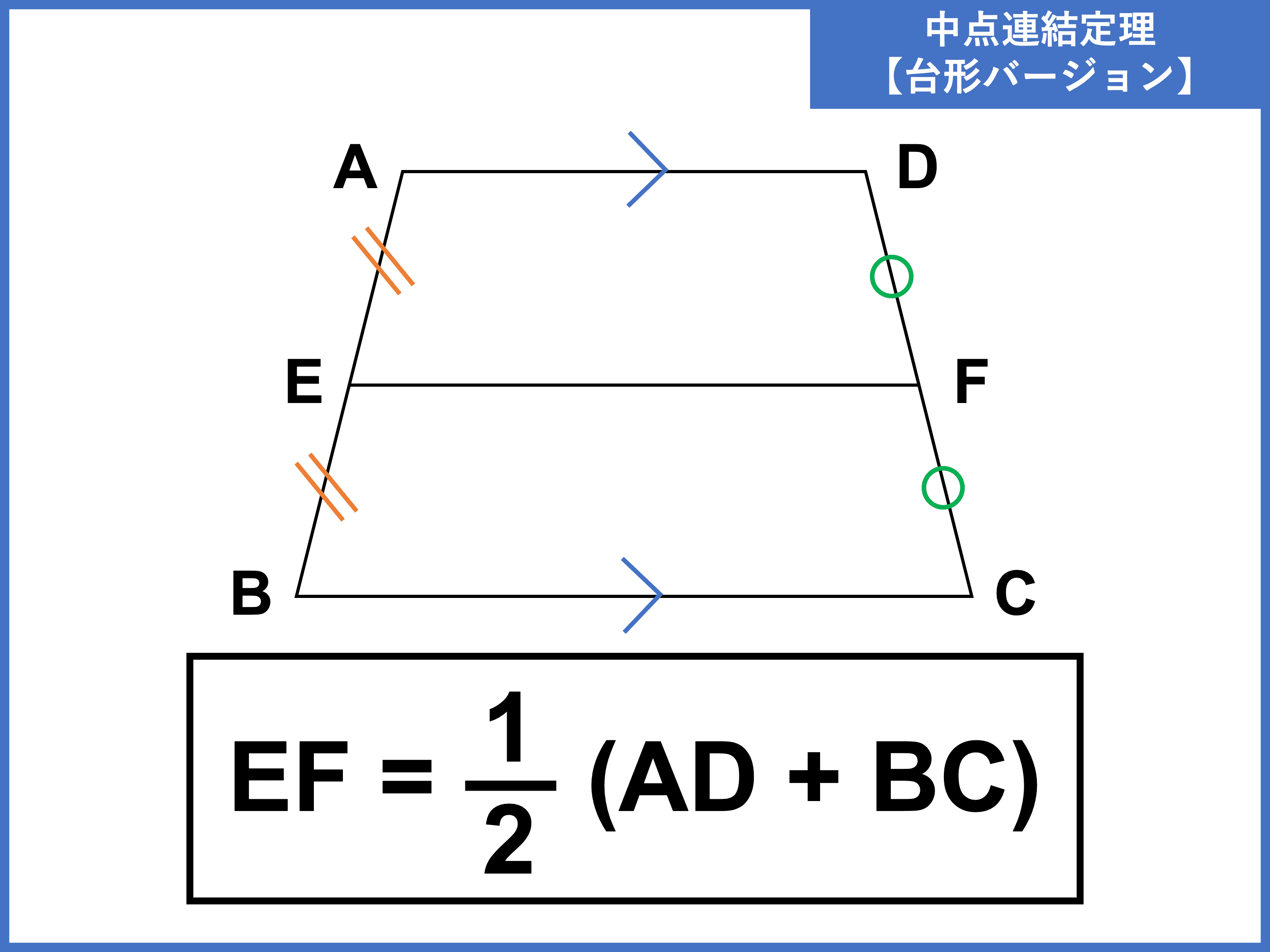
台形の中点連結定理の証明


四角形の中点連結定理

四角形の中点連結定理の証明



中点連結定理の計算問題
計算問題①「辺の長さを求める」


計算問題②「台形の中点を結ぶ」


計算問題③「平行四辺形であることを証明する」






最初の角度を求める例題 角ABCは、40度では?
この度はコメントいただきありがとうございます。
ご指摘の部分、図に合わせてテキストを修正いたしました。
今後ともどうぞ当サイトをよろしくお願いいたします。
証明①
AM:AB=1:2
AN:NCではなくAN:ACでは?
該当部分、修正いたしました。
チェックが行き届いておらず、申し訳ありません。
このようにご指摘いただけるととても助かります。
今後ともどうぞ当サイトをよろしくお願いいたします。