この記事では、「ドモアブルの定理」についてわかりやすく解説します。
証明や問題での使い方も説明しますので、この記事を通してぜひマスターしてくださいね。
目次
ドモアブルの定理とは?
ドモアブルの定理は、複素数のべき乗に関する以下の定理です。
任意の実数 \(\theta\)、任意の整数 \(n\) に対し、
\begin{align}\color{red}{(\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta}\end{align}
が成り立つ。
(ただし \(i\) は虚数単位)
つまり、複素数の \(n\) 乗が三角関数の \(n\) 倍角を使って表せます。
このとき、\(n\) が負の整数でも構いません。
ドモアブルの定理の図形的意味
よりイメージしやすいように、定理の図形的な意味を見ていきましょう。
絶対値 \(1\)、偏角 \(\theta\) の複素数 \(z\) について、\(z^2\), \(z^3\), \(z^4\) を計算すると
\(z = \cos \theta + i\sin \theta\) において、
ドモアブルの定理より
\(z^2 = \cos 2\theta + i\sin 2\theta\)
\(z^3 = \cos 3\theta + i\sin 3\theta\)
\(z^4 = \cos 4\theta + i\sin 4\theta\)
これらを複素平面上に図示すると以下のようになります。
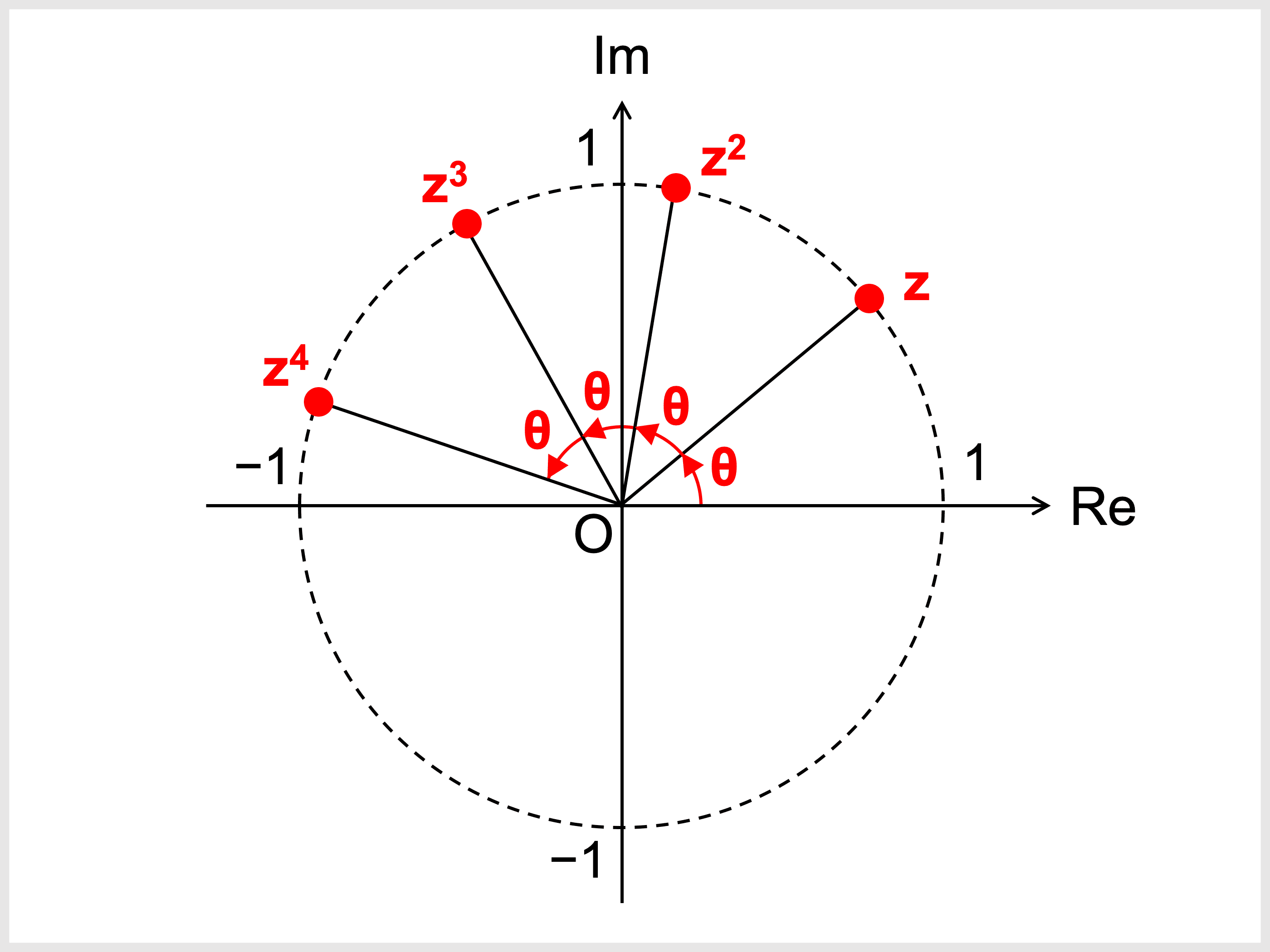
つまり、単位円上の複素数(絶対値 \(1\) の複素数)を \(n\) 乗すると偏角が \(n\) 倍になる、というのがドモアブルの定理です。
絶対値を \(0\) 以上の実数 \(r\) に拡張してあげれば、
\(\begin{align} z^n &= \{r(\cos \theta + i\sin \theta)\}^n \\ &= r^n(\cos \theta + i\sin \theta)^n \\ &= r^n (\cos n\theta + i\sin n\theta) \end{align}\)
と書けることになります。
したがって、「複素数の \(\bf{n}\) 乗は、絶対値を \(\bf{n}\) 乗し、偏角を \(\bf{n}\) 倍すればよい」ということですね。
ドモアブルの定理の利点
ドモアブルの定理が役に立つシーンを \(2\) つ紹介します。
【利点①】面倒な複素数のべき乗の展開を避けられる
これまで、複素数のべき乗 \((a + bi)^n\) は二項定理などを使って展開しなければならず、面倒でした。
ドモアブルの定理は、その計算の手間をほぼゼロにしてくれます。
例えば、\((1 + i)^4\) を二項定理で展開し、整理すると
\((1 + i)^4\)
\(= {}_4\mathrm{C}_0 \cdot 1^4 + {}_4\mathrm{C}_1 \cdot 1^3 \cdot i + {}_4\mathrm{C}_2 \cdot 1^2 \cdot i^2 \) \( + \,{}_4\mathrm{C}_3 \cdot 1 \cdot i^3 + {}_4\mathrm{C}_4 \cdot i^4\)
\(= 1 + 4i − 6 − 4i + 1\)
\(= −4\)
となる一方、複素数を極形式に直してドモアブルの定理を使うと、
\(\begin{align} (1 + i)^4 &= \left\{ \sqrt{2} \left( \cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \right) \right\}^4 \\ &= 4(\cos \pi + i\sin \pi) \\ &= −4 \end{align}\)
と、はるかに楽に計算できます。
二項定理による展開では、
- \(n\) が大きいと展開自体が面倒
- \(i\) をかける回数に応じて符号が変わるため、計算ミスしやすい
といった難点がありますが、ドモアブルの定理ならば面倒な展開も \(i\) の処理も不要です。
絶対値のべき乗はあるものの、正の実数のべき乗なのでそれほど難しくありません。
極形式に直すところさえクリアすれば、ドモアブルの定理を使う方が圧倒的に簡単で、計算ミスもしにくいです。
「複素数の極形式への変換」については、以下の記事で説明しています。
 複素数平面を総まとめ!数IIIで習う性質・公式一覧
複素数平面を総まとめ!数IIIで習う性質・公式一覧
【利点②】三角関数の n 倍角の公式を簡単に導ける
ドモアブルの定理「\((\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta\)」の両辺の実部、虚部を比較すると \(n\) 倍角の公式が導けます。
例えば \(n = 3\) とし、三倍角の公式を導いてみましょう。
\(n = 3\) のとき、
\((\cos \theta + i\sin \theta)^3 = \cos 3\theta + i\sin 3\theta\) …①
これが \(\theta\) に関する恒等式になるので、両辺の実部と虚部は等しいです。
左辺を展開し、右辺と比較します。
\((\cos \theta + i\sin \theta)^3\)
\(= \cos^3 \theta + 3i\cos^2 \theta \sin \theta \) \( − \,3\cos \theta \sin^2 \theta − i\sin^3 \theta\)
\(= \cos^3 \theta − 3\cos \theta \sin^2 \theta \) \( + \,i(3\cos^2 \theta \sin \theta − \sin^3 \theta)\)
①の右辺と比較すると
\(\cos^3 \theta − 3\cos \theta \sin^2 \theta = \cos 3\theta\) …②
\(3\cos^2 \theta \sin \theta − \sin^3 \theta = \sin 3\theta\) …③
②を整理すると
\(\cos 3\theta\)
\(= \cos^3 \theta − 3\cos \theta \sin^2 \theta\)
\(= \cos^3 \theta − 3\cos \theta (1 − \cos^2 \theta)\)
\(= \cos^3 \theta − 3\cos \theta + 3\cos^3 \theta\)
\(= 4\cos^3 \theta − 3\cos \theta\)
③を整理すると
\(\sin 3\theta\)
\(= 3\cos^2 \theta \sin \theta − \sin^3 \theta\)
\(= 3(1 − \sin^2 \theta)\sin \theta − \sin^3 \theta\)
\(= 3\sin \theta − 4\sin^3 \theta\)
よって
\(\color{red}{\cos 3\theta = 4\cos^3 \theta − 3\cos \theta}\)
\(\color{red}{\sin 3\theta = 3\sin \theta − 4\sin^3 \theta}\)
となり、\(\sin\) と \(\cos\) の三倍角の公式が導けました。
倍角の公式は数が多いので、公式の暗記に自信がない、ど忘れしやすいという人はこの方法も知っておくと便利ですね。
ドモアブルの定理の証明
ここでは、数学的帰納法を使ってドモアブルの定理を示します。
\((\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta\) …① を数学的帰納法で示す。
(i) \(n\) が自然数の場合 \((n > 0)\)
\(n = 1\) のとき
\((\text{左辺}) = \cos \theta + i\sin \theta = (\text{右辺})\)
となり、①は成り立つ。
\(n = k\) \((k \geq 1)\) のとき、①が成り立つと仮定すると、
\((\cos \theta + i\sin \theta)^k = \cos k\theta + i\sin k\theta\) …②
\(n = k + 1\) のときを考えると、
\((\cos \theta + i\sin \theta)^{k + 1}\)
\(= (\cos \theta + i\sin \theta)^k \cdot (\cos \theta + i\sin \theta)\)
\(= (\cos k\theta + i\sin k\theta)(\cos \theta + i\sin \theta)\) (②を利用)
\(= \cos k\theta\cos\theta − \sin k\theta\sin \theta \) \( + \,i(\sin k\theta\cos \theta + \cos k\theta \sin \theta)\)
\(= \cos (k + 1)\theta + i\sin (k + 1)\theta\) (加法定理を利用)
となり、すべての自然数について①は成り立つ。
(ii) \(n\) が \(0\) 以下の整数の場合 \((n \leq 0)\)
\(n = 0\) のとき
\((\text{左辺}) = (\text{右辺}) = 1\)
となり、①は成り立つ。
\(n \leq −1\) のとき
\(m = −n\) とおくと、\(m\) は自然数であるから①が成り立ち、
\((\cos \theta + i\sin \theta)^n\)
\(= \{(\cos \theta + i\sin \theta)^{−1}\}^m\)
\(= \{\cos(−\theta) + i\sin(−\theta)\}^m\)
\(= \cos(−m\theta) + i\sin(−m\theta)\)
\(= \cos n\theta + i\sin n\theta\)
以上より、すべての整数について ①(ドモアブルの定理)は成り立つ。
(証明終わり)
また、高校では習いませんが、オイラーの公式「\(e^{i\theta} = \cos \theta + i\sin \theta\)」を使うとより簡単にドモアブルの定理を証明できます。
\(e^{i\theta} = \cos \theta + i\sin \theta\) の両辺を \(n\) 乗して
\(e^{in\theta} = (\cos \theta + i\sin \theta)^n\) …(*)
(*) の左辺はオイラーの公式の左辺で \(\theta\) を \(n\theta\) に置き換えたものに等しいから、
\(e^{in\theta} = \cos n\theta + i\sin n\theta\)
よって
\((\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta\)
ドモアブルの定理の計算問題
最後に、ドモアブルの定理を使う問題に挑戦しましょう。
計算問題①「複素数のべき乗を計算する」
次の値を求めよ。
(1) \(\displaystyle \left( \cos \frac{\pi}{10} + i\sin \frac{\pi}{10} \right)^5\)
(2) \((1 + \sqrt{3} i)^{− 6}\)

どちらもドモアブルの定理を使えば楽に計算できます。
(2) では、まず()内を極形式で表しましょう。
(1)
\(\displaystyle \left( \cos \frac{\pi}{10} + i\sin \frac{\pi}{10} \right)^5\)
\(\displaystyle = \cos \frac{5\pi}{10} + i\sin \frac{5\pi}{10}\)
\(\displaystyle = \cos \frac{\pi}{2} + i\sin \frac{\pi}{2}\)
\(= i\)
答え: \(\color{red}{i}\)
(2)

\(|1 + \sqrt{3}i| = 2\) より
\(1 + \sqrt{3}i\)
\(\displaystyle = 2 \left( \frac{1}{2} + \frac{\sqrt{3}}{2}i \right)\)
\(\displaystyle = 2 \left( \cos \frac{\pi}{3} + i\sin \frac{\pi}{3} \right)\)
よって
\((1 + \sqrt{3}i)^{−6}\)
\(\displaystyle = \left\{ 2 \left( \cos \frac{\pi}{3} + i\sin \frac{\pi}{3} \right) \right\}^{−6}\)
\(=2^{−6} \{\cos (−2\pi) + i\sin (−2\pi)\}\)
\(= 2^{− 6}(1 + 0)\)
\(\displaystyle = \frac{1}{64}\)
答え: \(\color{red}{\displaystyle \frac{1}{64}}\)
計算問題②「\(z^4 + z^3 + z^2 + z + 1\) を求める」
\(\displaystyle z = \cos \frac{2}{5}\pi + i\sin \frac{2}{5}\pi\) のとき、\(z^4 + z^3 + z^2 + z + 1\) の値を求めよ。

求める式にそのまま \(z\) を代入してもうまくいきません。
式を変形してから代入する必要がありそうです。
「\(n\) 乗の差の因数分解の公式」を利用します。
\begin{align}\color{red}{a^n − b^n = (a − b)(a^{n−1} + a^{n−2}b + \cdots + ab^{n−2} + b^{n−1})}\end{align}
(見切れる場合は横へスクロール)
複素数分野では意外とよく使うので、これを機に覚えておきましょう!
\(z \neq 1\) より
\(\displaystyle z^4 + z^3 + z^2 + z + 1 = \frac{z^5 −1}{z − 1}\)
ここで、ドモアブルの定理より
\(\begin{align}\displaystyle z^5 &= \left(\cos \frac{2}{5}\pi + i\sin \frac{2}{5}\pi\right)^5\\&= \cos 2\pi + i\sin 2\pi \\&= 1\end{align}\)
よって
\(z^5 − 1 = 0\)
\(\displaystyle \frac{z^5 −1}{z − 1} = 0\)
したがって、
\(z^4 + z^3 + z^2 + z + 1 = 0\)
答え: \(\color{red}{0}\)
以上で今回の記事は終わりです。
ドモアブルの定理をマスターして、複素数分野を得意に変えましょう!

