数III「複素数平面」について、さまざまな公式や性質を図形を示しながらわかりやすくまとめています。
関連記事へのリンクも示しているので、ぜひ複素数平面の理解に役立ててくださいね!
目次
複素数平面とは?
複素数平面とは、複素数 \(z = x + yi\) を点 \((x, y)\) に対応させた直交座標平面のことです。

今まで扱っていた \(xy\) 平面上の各点は単に「\(2\) つの実数の組 \((x, y)\)」を表していますが、複素数平面では「\(1\) つの複素数」を表すというわけです。
実部 \(x\) に対応する横軸を「実軸」、虚部 \(y\) に対応する縦軸を「虚軸」といいます。
実軸は Re (Real part) 、虚軸は Im (Imaginally part) と表すことが多いです。
複素数
\(2\) つの実数 \(a\), \(b\) と虚数単位 \(i\) を用いて \(z = a + bi\) と表せる数のこと。
\(a\) を \(z\) の実部、\(b\) を \(z\) の虚部という。
 複素数とは?公式や i の 2 乗の意味、計算問題の解き方
複素数とは?公式や i の 2 乗の意味、計算問題の解き方
共役複素数
\(z = x + yi\) に対し、\(\color{red}{\overline{z} = x − yi}\) を \(z\) の共役複素数といいます。
複素数平面において、\(z\) は点 \((x, y)\) に、\(\overline{z}\) は点 \((x, −y)\) に対応します。
つまり、\(z\) と \(\overline{z}\) は実軸対称な位置にあります。

複素数の対称移動
よって、複素数の対称移動は次のように表せます。
複素数 \(z = x + yi\) について、
- 実軸に関して対称移動した点
→ \(\color{red}{\overline{z} = x − yi}\) - 虚軸に関して対称移動した点
→ \(\color{red}{−\overline{z} = −x + yi}\) - 原点に関して対称移動した点
→ \(\color{red}{−z = −x − yi}\)

共役な複素数の性質
また、共役な複素数同士には次の性質が成り立ちます。
\(z\), \(w\) を複素数とすると、以下が成り立つ。
- 共役複素数の和と差
\(z + \overline{z}\) は実数
\(z − \overline{z}\) は純虚数または \(0\) - 実数、純虚数の共役
\(z\) が実数 \(\iff\) \(z = \overline{z}\)
\(z\) が純虚数 \(\iff\) \(z = −\overline{z}\) かつ \(z \neq 0\) - 和・差・積・商の共役
\(\overline{z + w} = \overline{z} + \overline{w}\)
\(\overline{z − w} = \overline{z} − \overline{w}\)
\(\overline{zw} = \overline{z} \cdot \overline{w}\)
\(\displaystyle \overline{\left( \frac{z}{w} \right)} = \frac{\overline{z}}{\overline{w}}\) (\(w \neq 0\)) - 共役の共役
\(\overline{\overline{z}} = z\)
性質 1, 2 は問題を解く際の重要な条件になることもあるので、押さえておきましょう。
また、性質 3 で示すように、共役を示す \(\overline{ }\) の記号は分配・統合できます。
\(z = a + bi\), \(w = c + di\)(\(a\), \(b\), \(c\), \(d\) は実数)とおき、それぞれを簡単に示します。
- 共役複素数の和
\(z + \overline{z} = (a + bi) + (a − bi) = 2a\)
より、\(z + \overline{z}\) は実数 - 共役複素数の差
\(z − \overline{z} = (a + bi) − (a − bi) = 2bi\)
より、\(z − \overline{z}\) は純虚数または \(0\)
(証明終わり)
- 実数の共役
\(z = a + bi\) が実数
\(\iff b = 0\)
\(\iff\) \(a + bi = a − bi\)
\(\iff\) \(z = \overline{z}\) - 純虚数の共役
\(z = a + bi\) が純虚数
\(\iff\) \(a = 0\) かつ \(b \neq 0\)
\(\iff\) \(a + bi = −a + bi\) かつ \(b \neq 0\)
\(\iff\) \(z = −\overline{z}\) かつ \(z \neq 0\)
(証明終わり)
- 和の共役
\(z + w = (a + c) + (b + d)i\) より、
\(\begin{align} \overline{z + w} &= (a + c) − (b + d)i \\ &= (a − bi) + (c − di) \\ &= \overline{z} + \overline{w} \end{align}\) - 差の共役
\(z − w = (a − c) + (b − d)i\) より、
\(\begin{align} \overline{z − w} &= (a − c) − (b − d)i \\ &= (a − bi) − (c − di) \\ &= \overline{z} − \overline{w} \end{align}\) - 積の共役
\(\begin{align} zw &= (a + bi)(c + di) \\ &= ac − bd + (ad + bc)i \end{align}\)
より
\(\overline{zw} = ac − bd − (ad + bc)i\)
また、
\(\begin{align} \overline{z} \cdot \overline{w} &= (a − bi)(c − di) \\ &= ac − bd − (ad + bc)i \end{align}\)
よって
\(\overline{zw} = \overline{z} \cdot \overline{w}\) - 商の共役
\(w \neq 0\) のとき、
\(\begin{align} \frac{z}{w} &= \frac{a + bi}{c + di} \\ &= \frac{(a + bi)(c − di)}{(c + di)(c − di)} \\ &= \frac{ac + bd − (ad − bc)i}{c^2 + d^2} \end{align}\)
より、
\(\displaystyle \overline{\left( \frac{z}{w} \right)} = \frac{ac + bd + (ad − bc)i}{c^2 + d^2}\)
また、
\(\begin{align} \frac{\overline{z}}{\overline{w}} &= \frac{a − bi}{c − di} \\ &= \frac{(a − bi)(c + di)}{(c − di)(c + di)} \\ &= \frac{ac + bd + (ad − bc)i}{c^2 + d^2} \end{align}\)
よって
\(\displaystyle \overline{\left( \frac{z}{w} \right)} = \frac{\overline{z}}{\overline{w}}\)
(証明終わり)
共役の共役
\(\begin{align} \overline{\overline{z}} &= \overline{a − bi} \\ &= a + bi \\ &= z \end{align}\)
(証明終わり)
複素数の絶対値
複素数平面において、\(z = x + yi\) に対応する点 \((x, y)\) と原点 \(\mathrm{O}\) との距離を \(z\) の絶対値といい、\(\color{red}{|z|}\) と表します。
\(z = x + yi\) のとき、\(z\) に対応する点 \((x, y)\) と原点 \(\mathrm{O}\) との距離は
\begin{align}\color{red}{|z| = |x + yi| = \sqrt{x^2 + y^2}}\end{align}

複素数平面における二点間の距離
したがって、\(2\) 点間の距離は絶対値を使って以下のように求められます。
複素数 \(z = a + bi\), \(w = c + di\) に対応する点 \((a, b)\), \((c, d)\) の距離は
\begin{align}\color{red}{|w − z| = \sqrt{(c − a)^2 + (d − b)^2}}\end{align}

複素数の絶対値の性質
また、次の絶対値の性質も押さえておきましょう。
\(z\), \(w\) を複素数とすると、以下が成り立つ。
- \(\color{red}{|z| = 0 \iff z = 0}\)
- \(|z| = |−z| = |\overline{z}|\) より
\(\color{red}{z\overline{z} = |z|^2}\)
- \(\color{red}{|zw| = |z||w|}\)
- \(\color{red}{\displaystyle \left| \frac{z}{w} \right| = \frac{|z|}{|w|}}\) (\(w \neq 0\))
複素数の計算では頻繁に絶対値を扱うので、どれも確実に理解しておきましょう。
\(z = a + bi\), \(w = c + di\)(\(a\), \(b\), \(c\), \(d\) は実数)とおき、それぞれを簡単に示します。
\(\begin{align}|z| = 0 &\iff \sqrt{a^2 + b^2} = 0\\&\iff a = 0, b = 0\\&\iff z = 0\end{align}\)
(証明終わり)
\(\begin{align} z\overline{z} &= (a + bi)(a − bi) \\ &= a^2 + b^2 \\ &= |z|^2 \end{align}\)
(証明終わり)
性質 2 より、
\(\begin{align} |zw|^2 &= zw\overline{zw} \\ &= z\overline{z}w\overline{w} \\ &= |z|^2|w|^2 \end{align}\)
\(|zw| \geq 0\), \(|z||w| \geq 0\) より、
\(|zw| = |z||w|\)
(証明終わり)
\(w \neq 0\) のとき、\(\displaystyle w \cdot \frac{z}{w} = z\) であるから、
性質 3 より
\(\begin{align} \left| w \cdot \frac{z}{w} \right| &= |w| \left| \frac{z}{w} \right| \\ &= |z| \end{align}\)
よって
\(\displaystyle \left| \frac{z}{w} \right| = \frac{|z|}{|w|}\)
(証明終わり)
極形式
複素数平面において、ある点の座標 \((x, y)\) は原点からの距離(= 絶対値)と角度で表すことができ、これを「極形式」といいます。
このとき、原点と点 \((x, y)\) を結ぶ直線が実軸の正の向きとなす角を偏角といい、\(\color{red}{\arg(z)}\)(または \(\color{red}{\theta}\))と表します。
複素数 \(z = x + yi\) について、偏角を \(\theta\) とすると、
\(x = |z|\cos\theta\), \(y = |z|\sin\theta\) より、\(z\) を極形式で表すと
\begin{align}\color{red}{z = |z|(\cos\theta + i\sin\theta)}\end{align}

ちなみに、極形式において絶対値を「\(r\)」と表すことも多いので見慣れておきましょう。
(例)
絶対値 \(r\)、偏角 \(\theta\) の複素数 \(z\)
\(z = r(\cos\theta + i\sin\theta)\)
極形式は、「極座標」や「極方程式」の考え方がベースになっています。
よくわからないという人は以下の記事で学習しておきましょう!
 極座標とは?直交座標との表示変換、距離や面積の公式
極座標とは?直交座標との表示変換、距離や面積の公式
 極方程式とは?グラフの書き方や面積・曲線の長さの公式
極方程式とは?グラフの書き方や面積・曲線の長さの公式
複素数の四則演算の公式
ここからは、複素数の四則演算と複素数平面における意味を説明していきます。
複素数の加法・減法
複素数の足し算・引き算は、ベクトルと同じように考えることができます。
\(z_1 = x_1 + y_1i\), \(z_2 = x_2 + y_2i\) とする。
- 加法
\(w = z_1 + z_2\) とすると
\(\color{red}{w = (x_1 + x_2) + (y_1 + y_2)i}\) - 減法
\(w = z_1 − z_2\) とすると
\(\color{red}{w = (x_1 − x_2) + (y_1 − y_2)i}\)

式変形もグラフも、成分ベクトルの和や差とそっくりです。
このようなベクトルとの対応を頭に入れておくと今後の理解に役立ちます。
一方で、乗法と除法ではベクトルのように考えることができないため、極形式を利用します。
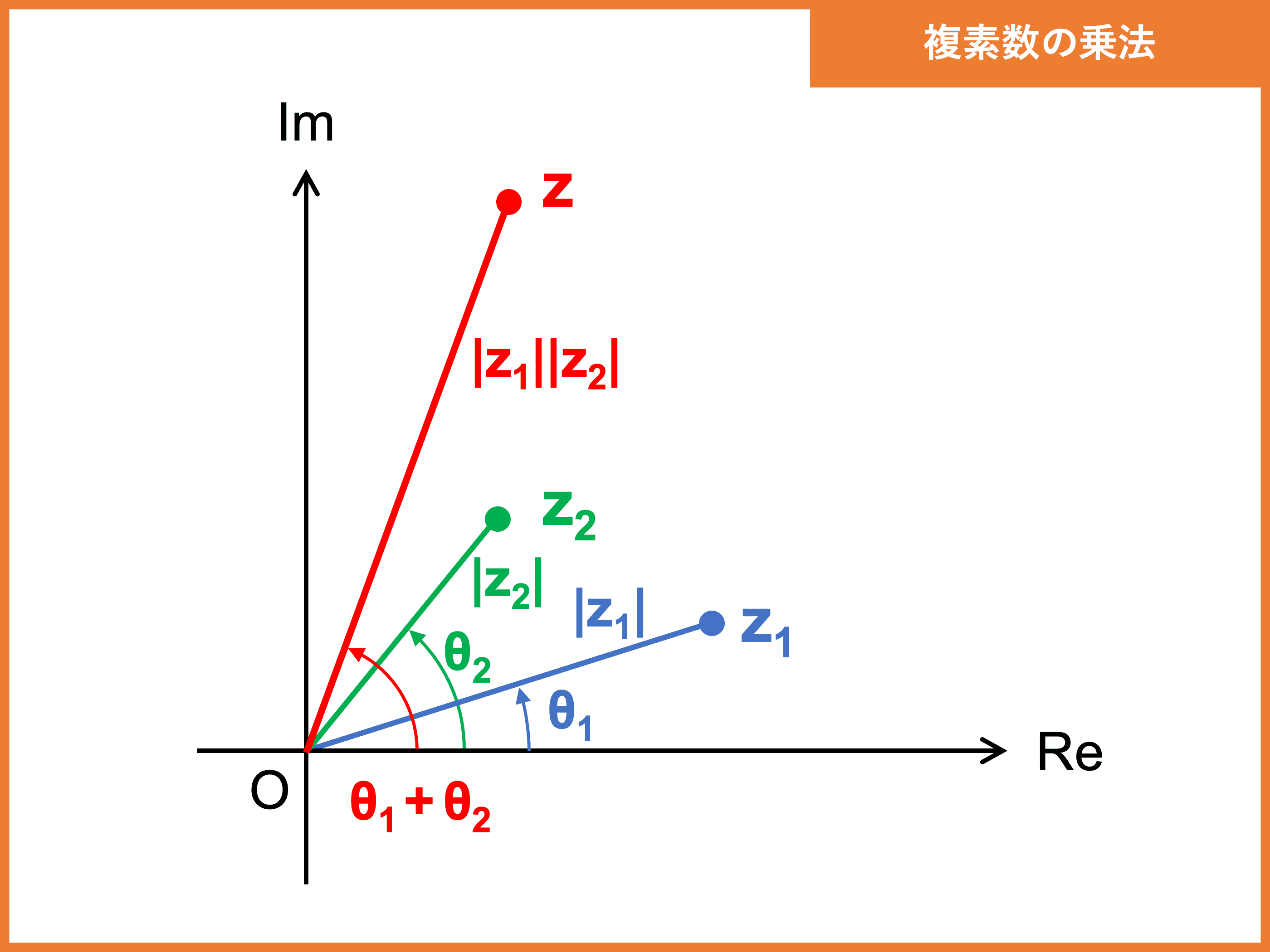
複素数の乗法
複素数同士のかけ算は、極形式で考えると絶対値(距離)のかけ算、偏角の足し算になります。
\(z_1 = |z_1|(\cos\theta_1 + i\sin\theta_1)\), \(z_2 = |z_2|(\cos\theta_2 + i\sin\theta_2)\) とすると、積 \(z_1z_2\) は
\begin{align}\color{red}{z_1z_2 = |z_1||z_2|(\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2))}\end{align}
(見切れる場合は横へスクロール)
これは、式を展開し、加法定理を利用して導けます。
(見切れる場合は横へスクロール)
\(z_1z_2\)
\(= |z_1||z_2|(\cos \theta_1 + i\sin \theta_1)(\cos \theta_2 + i\sin \theta_2)\)
\(= |z_1||z_2|\{\color{orange}{\cos \theta_1\cos \theta_2 − \sin \theta_1\sin \theta_2 } + \,i(\color{skyblue}{\sin \theta_1\cos \theta_2 + \sin \theta_2\cos \theta_1})\}\)
\(= |z_1||z_2|(\color{orange}{\cos(\theta_1 + \theta_2}) + i\color{skyblue}{\sin(\theta_1 + \theta_2}))\)
(加法定理)
(証明終わり)
よって、ある複素数に別の複素数 \(r(\cos \theta + i\sin \theta)\) をかけることは、複素数平面上で原点中心に \(\theta\) だけ回転して絶対値を \(r\) 倍することと等価です。
複素数の除法
複素数同士の割り算は、極形式で考えると絶対値(距離)の割り算、偏角の引き算になります。
\(z_1 = |z_1|(\cos \theta_1 + i\sin \theta_1)\), \(z_2 = |z_2|(\cos \theta_2 + i\sin \theta_2)\) とすると、商 \(\displaystyle \frac{z_1}{z_2}\) は
\begin{align}\color{red}{\displaystyle \frac{z_1}{z_2} = \frac{|z_1|}{|z_2|} (\cos(\theta_1 − \theta_2) + i\sin(\theta_1 − \theta_2))}\end{align}

途中、分母を有理化すると乗法と同様に加法定理を利用して導けます。
(見切れる場合は横へスクロール)
\(\displaystyle \frac{z_1}{z_2}\)
\(\displaystyle = \frac{|z_1|(\cos \theta_1 + i\sin \theta_1)}{|z_2|(\cos \theta_2 + i\sin \theta_2)}\)
\(\displaystyle = \frac{|z_1|}{|z_2|}\frac{\cos \theta_1 + i\sin \theta_1}{\cos \theta_2 + i\sin \theta_2}\)
\(\displaystyle = \frac{|z_1|}{|z_2|}\frac{(\cos \theta_1 + i\sin \theta_1)(\cos \theta_2 − i\sin \theta_2)}{\cos^2 \theta_2 + \sin^2 \theta_2}\)
(分母の実数化)
\(\displaystyle = \frac{|z_1|}{|z_2|} \{\color{orange}{\cos \theta_1\cos \theta_2 + \sin \theta_1\sin \theta_2} + i(\color{skyblue}{\sin \theta_1\cos \theta_2 − \cos \theta_1\sin \theta_2})\}\)
\(\displaystyle = \frac{|z_1|}{|z_2|} (\color{orange}{\cos(\theta_1 − \theta_2}) + i\color{skyblue}{\sin(\theta_1 − \theta_2}))\)
(加法定理)
(証明終わり)
よって、ある複素数を別の複素数 \(r(\cos \theta + i\sin \theta)\) で割ることは、複素数平面上で原点中心に \(−\theta\) だけ回転して絶対値を \(\displaystyle \frac{1}{r}\) 倍することと等価です。
乗法とセットで覚えておきましょう!
後ほど解説するドモアブルの定理を利用すると、乗法と除法でやっていることは基本的に同じと考えることができます。
\(\displaystyle \frac{1}{z} = z^{−1} = \frac{1}{r} (\cos(−\theta) + i\sin(−\theta))\)
より、
\begin{align} \frac{z_1}{z_2} &= z_1 \cdot \frac{1}{z_2} \\ &= \frac{|z_1|}{|z_2|} (\cos(\theta_1 − \theta_2) + i\sin(\theta_1 − \theta_2)) \end{align}
複素数の回転移動
複素数の乗法・除法の性質から、複素数をかけたり割ったりすることは、原点まわりの拡大・縮小と回転を意味していることがわかります。
- 複素数 \(z\) に \(w = r(\cos \theta + i\sin \theta)\) をかける
\(z\) は原点からの距離が \(r\) 倍、偏角が原点中心に \(+\theta\) 回転した点に移動 - 複素数 \(z\) を \(w = r(\cos \theta + i\sin \theta)\) で割る
\(z\) は原点からの距離が \(\displaystyle \frac{1}{r}\) 倍、偏角が原点中心に \(−\theta\) 回転した点に移動
ここでは、回転だけにフォーカスして
- 原点中心の回転
- 原点中心でない回転
について考えていきます。
原点中心の回転
複素数平面上のある点を原点中心に \(\theta\) だけ回転させるには、絶対値が \(1\) の複素数 \(\cos \theta + i\sin \theta\) をかければよいですね。
複素数 \(z = |z|(\cos \theta_z + i\sin \theta_z)\) を複素数平面上で原点を中心に \(\theta\) 回転させた複素数 \(z’\) は
\begin{align}z’ &= z\color{red}{(\cos \theta + i\sin \theta)} \\ &= |z| \{\cos(\theta_z \color{red}{+ \theta}) + i\sin(\theta_z \color{red}{+ \theta})\}\end{align}

原点中心でない回転
それでは、原点中心でない回転はどのように表せるでしょうか?
複素数 \(z\) を、点 \(\alpha\) を中心に \(\theta\) だけ回転させる操作は次の通りです。
- \(\alpha\) が原点に重なるように \(z\) と \(\alpha\) を平行移動する
- \(z − \alpha\) を原点 \(\mathrm{O}\) 中心に \(\theta\) だけ回転する
- \(\alpha\) が元の位置に戻るように再び平行移動する

これを式で表すと、以下のようになります。
複素数 \(z\) を複素数平面上で点 \(\alpha\) を中心に \(\theta\) 回転させた複素数 \(z’\) は
\begin{align}z’ = (z \color{red}{− \alpha})\color{red}{(\cos \theta + i\sin \theta) + \alpha}\end{align}
平行移動 → 回転 → 平行移動のプロセスと式を照らし合わせて覚えましょう!
極形式と公式
ここでは、複素数の極形式に関する公式を説明します。
ドモアブルの定理
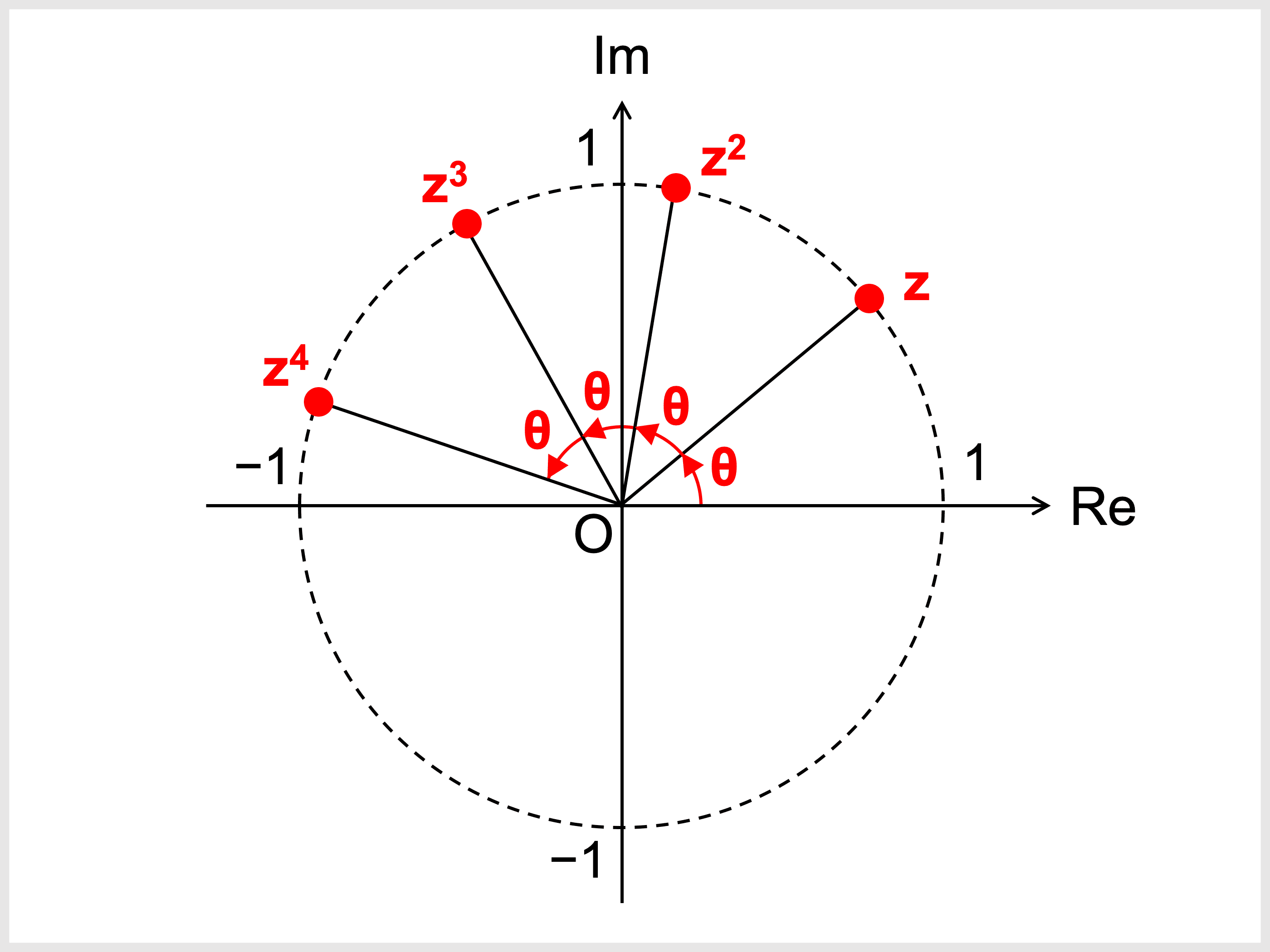
ドモアブルの定理は、複素数のべき乗に関する定理です。
任意の実数 \(\theta\)、任意の整数 \(n\) に対し
\begin{align}\color{red}{(\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta}\end{align}
が成り立つ。
(ただし \(i\) は虚数単位)
先ほど、\(\cos \theta + i\sin \theta\) をかけることは原点中心に \(\theta\) 回転させることであると確認しました。
それを踏まえると、左辺は「\(1\) が表す点に \(\theta\) 回転を \(n\) 回加える」と解釈でき、わかりやすいですね。
なお、「ドモアブルの定理」については以下の記事でより詳しく解説しています。
 ドモアブルの定理とは?意味や証明、問題の解き方
ドモアブルの定理とは?意味や証明、問題の解き方
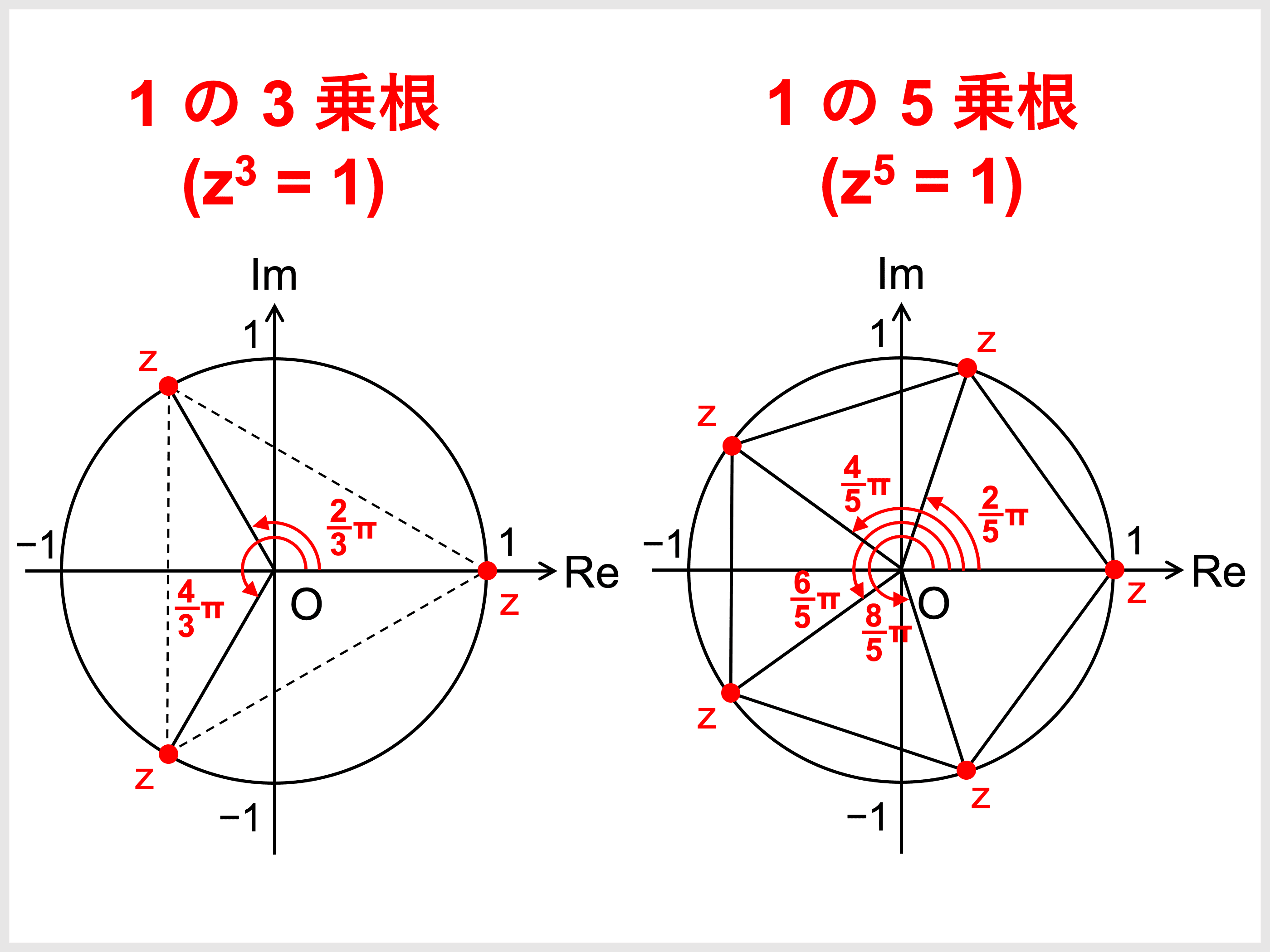
\(1\) の \(n\) 乗根
複素数 \(z\) が \(\color{red}{z^n = 1}\) を満たすとき、\(z\) を「\(1\) の \(n\) 乗根」といいます。
\(1\) の \(n\) 乗根について、一般に次が成り立ちます。
\(1\) の \(n\) 乗根は、次の \(n\) 個の複素数 \(z_k\) \((k = 0, 1, \cdots, n−1)\) である。
\begin{align}\color{red}{\displaystyle z_k = \cos\frac{2k\pi}{n} + i\sin\frac{2k\pi}{n}}\end{align}
\(1\) の \(n\) 乗根は \(n\) 個存在し、複素数平面上に図示すると \(z = 1\) を \(1\) 頂点として含み、他の頂点もすべて単位円上に存在する正 \(n\) 角形になります。
この関係を、極形式で導いてみましょう。
\(z^n = 1\) のとき、\(|z| = 1\) より
\(z = \cos \theta + i\sin \theta\) \((0 \leq \theta \leq 2\pi)\) と書ける。
ドモアブルの定理より、
\(z^n = \cos n\theta + i\sin n\theta\)
これが \(1\) であるとすると、
\(\cos n\theta = 1\), \(\sin n\theta = 0\)
これを満たす \(n\theta\) \((0 \leq n\theta \leq 2n\pi)\) は
\(n\theta = 2k\pi\) \((k = 0, 1, 2, \cdots)\)
よって
\(\displaystyle \theta = \frac{2k\pi}{n}\) \((k = 0, 1, 2, \cdots)\)
\(0 \leq n\theta \leq 2n\pi\) でこれを満たす \(\theta\) を書き出すと
\(\displaystyle \theta = 0, \frac{2\pi}{n}, \frac{4\pi}{n}, \cdots, \frac{2(n − 2)\pi}{n}, \frac{2(n − 1)\pi}{n}\)
(証明終わり)
このように、条件を満たす \(\theta\) は \(n\) 個存在するとわかり、\(1\) の \(n\) 乗根は \(n\) 個存在します。
オイラーの公式
高校では習いませんが、非常に有名で、知っておく価値のある公式です。
任意の偏角 \(\theta\) について、
\begin{align}\color{red}{e^{i\theta} = \cos\theta + i\sin\theta}\end{align}
詳しくは以下の記事で説明しています。
 オイラーの公式とは?証明やオイラーの等式との関係
オイラーの公式とは?証明やオイラーの等式との関係
複素数平面の練習問題
最後に複素数平面の練習問題に挑戦しましょう。
練習問題①「極形式で表し、図示せよ」
\(z = 1 + \sqrt{3}i\) のとき、以下の複素数を極形式で表し、複素数平面上に図示せよ。
(1) \(z\) (2) \(\overline{z}\) (3) \(\displaystyle \frac{1}{z}\)

実際に実部と虚部を取り出して複素数平面上に図示してみると、絶対値と偏角がわかりやすいですよ。
\(|z| = 2\) より
\(\begin{align} z &= 2 \left( \frac{1}{2} + i\frac{\sqrt{3}}{2} \right) \\ &=2 \left( \cos \frac{\pi}{3} + i\sin \frac{\pi}{3} \right) \end{align}\)
よって
\(\begin{align} \overline{z} &= 2 \left( \cos \frac{\pi}{3} − i\sin \frac{\pi}{3} \right) \\ &= 2 \left( \cos\left( −\frac{\pi}{3} \right) + i\sin\left( −\frac{\pi}{3} \right) \right) \end{align}\)
\(\begin{align} \frac{1}{z} &= z^{−1} \\ &= \frac{1}{2} \left( \cos\left( −\frac{\pi}{3} \right) + i\sin\left( −\frac{\pi}{3} \right) \right) \end{align}\)
これらを図示すると以下の通り。
答え:

\(\color{red}{\displaystyle z = 2\left( \cos \frac{\pi}{3} + i\sin \frac{\pi}{3} \right)}\)
\(\color{red}{\displaystyle \overline{z} = 2\left( \cos\left( −\frac{\pi}{3} \right) + i\sin\left( −\frac{\pi}{3} \right) \right)}\)
\(\color{red}{\displaystyle \frac{1}{z} = \frac{1}{2} \left( \cos\left( −\frac{\pi}{3} \right) + i\sin\left( −\frac{\pi}{3} \right) \right)}\)
練習問題②「ある点が表す複素数を求める」
(1) \(z = 1 − i\) を原点中心に \(\displaystyle \frac{\pi}{2}\) 回転させた点が表す複素数を求めよ。
(2) \(z = 1 − i\) を \(1\) が表す点を中心に \(\displaystyle \frac{\pi}{2}\) 回転させた点が表す複素数を求めよ。

回転の問題です。
極形式と通常の形をうまく使い分けましょう。
(1)
求める複素数を \(z’\) とすると、
\(\begin{align} z’ &= z\left( \cos \frac{\pi}{2} + i\sin \frac{\pi}{2} \right) \\&= (1 − i)(0 + i \cdot 1) \\&= (1 − i)i \\&= 1 + i\end{align}\)
答え: \(\color{red}{1 + i}\)
(2) 求める複素数を \(z’’\) とすると
\(\begin{align} z’’ &= (z − 1) \left( \cos\frac{\pi}{2} + i\sin\frac{\pi}{2} \right) + 1 \\ &= (−i) \cdot i + 1 \\ &= 2 \end{align}\)
答え: \(\color{red}{2}\)
練習問題③「方程式の解を複素数平面に図示せよ」
\(z^3 = 2 + 2i\) の解を極形式で表し、複素数平面上に図示せよ。

複素数の方程式は通常の形で解く方が良い場合もありますが、べき乗を処理するときなどは極形式を使うと楽になります。
(見切れる場合は横へスクロール)
\(z = r(\cos\theta + i\sin\theta)\) \((r > 0\), \(0 \leq \theta < 2\pi)\) とおくと、
ドモアブルの定理から
\(z^3 = r^3(\cos 3\theta + i\sin 3\theta)\) …①
一方、\(|2 + 2i| = 2\sqrt{2}\) より
\(z^3\)
\(= 2 + 2i\)
\(\displaystyle = 2\sqrt{2} \left( \frac{1}{\sqrt{2}} + \frac{i}{\sqrt{2}} \right)\)
\(\displaystyle = 2\sqrt{2} \left( \cos\left( \frac{\pi}{4} + 2n\pi \right) + i\sin\left( \frac{\pi}{4} + 2n\pi \right) \right)\) \((n = 0, 1, 2, \cdots)\) …②
①、②を比較すると
\(r^3 = 2\sqrt{2}\), \(\displaystyle 3\theta = \frac{\pi}{4} + 2n\pi\)
よって
\(r = \sqrt{2}\), \(\displaystyle \theta = \frac{\frac{\pi}{4} + 2n\pi}{3}\)
\(0 \leq \theta < 2\pi\) より
\(\displaystyle \theta = \frac{\pi}{12}, \frac{9\pi}{12} \left( = \frac{3}{4} \pi \right), \frac{17\pi}{12}\)
したがって、
\(\displaystyle z \) \(\displaystyle = \sqrt{2} \left( \cos\frac{\frac{\pi}{4} + 2m\pi}{3} + i\sin\frac{\frac{\pi}{4} + 2m\pi}{3} \right)\) \((m = 0, 1, 2)\)
これを図示すると以下の通り。
答え:

\(\begin{align}\color{red}{z = } &\color{red}{\sqrt{2} \left( \cos\frac{\pi}{12} + i\sin\frac{\pi}{12} \right),}\\& \color{red}{\sqrt{2} \left( \cos\frac{3}{4}\pi + i\sin\frac{3}{4}\pi \right),}\\& \color{red}{\sqrt{2} \left( \cos\frac{17}{12}\pi + i\sin\frac{17}{12}\pi \right)}\end{align}\)
以上で複素数平面の解説は終わりです。
はじめは取っつきにくく感じますが、慣れれば比較的単純です。
練習を重ねて複素数平面を得意分野にしていきましょう!
