この記事では、漸化式全 12 パターンの解き方と例題をまとめて、わかりやすく解説しています。
各パターンの攻略法をマスターして、難しい問題にも対応できるようになりましょう!
目次
- 漸化式のパターン一覧
- 隣接二項間漸化式の解き方
- 等差型 \(a_{n + 1} = a_n + d\)
- 等比型 \(a_{n + 1} = ra_n\)
- 階差型 \(a_{n + 1} = a_n + f(n)\)
- 特殊解型 \(a_{n + 1} = pa_n + q\)
- \(n\) 次式型 \(a_{n + 1} = pa_n + f(n)\)
- 階比型 \(a_{n + 1} = f(n)a_n\)
- 指数型 \(a_{n + 1} = pa_n + q \cdot r^n\)
- 対数型 \(a_{n + 1} = pa_n^q\)
- 逆数型 \(\displaystyle a_{n + 1} = \frac{pa_n}{qa_n + r}\)
- 一次分数型 \(\displaystyle a_{n + 1} = \frac{pa_n + q}{ra_n + s}\)
- 隣接三項間漸化式の解き方
漸化式のパターン一覧
高校で習う主要な漸化式のパターン一覧(隣接二項間漸化式 10 パターン、隣接三項間漸化式 2 パターン)をまとめました。
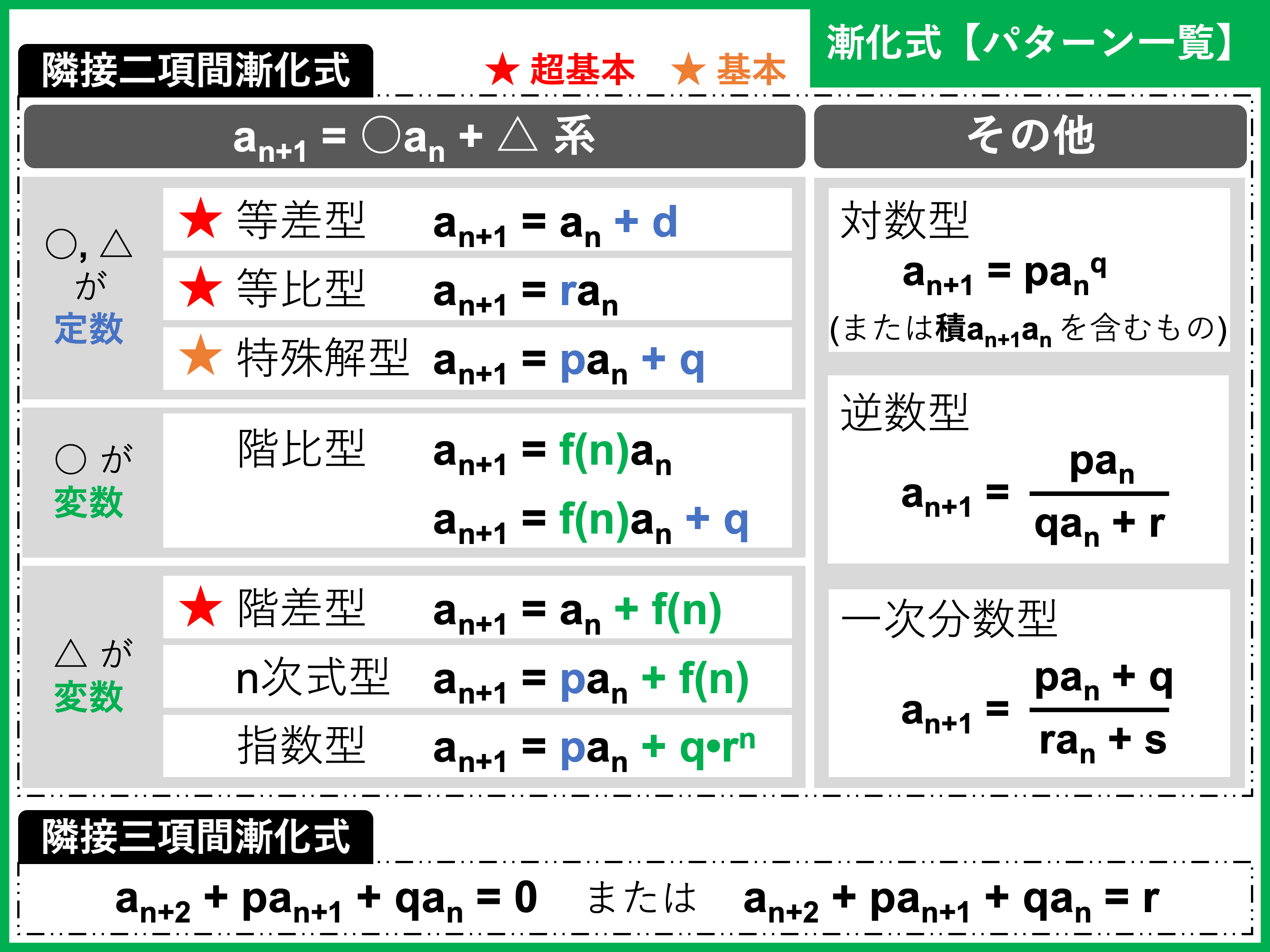
隣接二項間漸化式のうち、等差型・等比型・階差型の \(3\) つは基本中の基本、特殊解型は基本です。必ず押さえましょう!
基本 \(3\) 型(等差・等比・階差型)および特殊解型の漸化式について詳しく説明しています。
 漸化式とは?基本型や特性方程式をわかりやすく解説!
漸化式とは?基本型や特性方程式をわかりやすく解説!
それでは、各パターンの漸化式の解き方をすべて解説していきます!
隣接二項間漸化式の解き方
隣接二項間漸化式の解き方を説明します。
等差型 \(a_{n + 1} = a_n + d\)
基本 \(3\) 型(等差・等比・階差型)の \(1\) つです。
等差型の漸化式を見たらただちに一般項の公式に当てはめましょう。
漸化式 \(a_{n + 1} = a_n + d\)
→ 初項 \(a_1\)、公差 \(d\) の等差数列
一般項 \(a_n = a_1 + (n − 1)d\)
\(a_1 = 1\), \(a_{n + 1} = a_n + 2\) によって定められる数列 \(\{a_n\}\) の一般項を求めよ。
初項 \(1\)、公差 \(2\) の等差数列であるから、
一般項は
\(\begin{align} a_n &= 1 + (n − 1)2 \\ &= 2n − 1 \end{align}\)
答え: \(\color{red}{a_n = 2n − 1}\)
等比型 \(a_{n + 1} = ra_n\)
基本 \(3\) 型(等差・等比・階差型)の \(1\) つです。
等比型の漸化式を見たらただちに一般項の公式に当てはめましょう。
漸化式 \(a_{n + 1} = ra_n\)
→ 初項 \(a_1\)、公比 \(r\) の等比数列
一般項 \(a_n = a_1r^{n − 1}\)
\(a_1 = 2\), \(a_{n + 1} = 3a_n\) によって定められる数列 \(\{a_n\}\) の一般項を求めよ。
初項 \(2\)、公比 \(3\) の等比数列であるから、
一般項は
\(a_n = 2 \cdot 3^{n − 1}\)
答え: \(\color{red}{a_n = 2 \cdot 3^{n − 1}}\)
階差型 \(a_{n + 1} = a_n + f(n)\)
基本 \(3\) 型(等差・等比・階差型)の \(1\) つです。
階差型の漸化式を見たらただちに一般項の公式に当てはめましょう。
漸化式 \(a_{n + 1} = a_n + f(n)\)
→ 初項 \(a_1\) で、階差数列 \(b_n = f(n)\) をもつ数列
一般項 \(a_n = \left\{\begin{array}{l} \displaystyle a_1 + \sum_{k = 1}^{n − 1} f(k) \quad (n \geq 2) \\ a_1 \quad (n = 1) \end{array}\right.\)
\(a_1 = 2\), \(a_{n + 1} = a_n − 3n + 1\) によって定められる数列 \(\{a_n\}\) の一般項を求めよ。
\(a_{n + 1} − a_n = −3n + 1\)
より、\(\{a_n\}\) は一般項が \(−3n + 1\) の階差数列をもつ。
よって、\(n \geq 2\) のとき
\(\begin{align} a_n &= a_1 + \sum_{k = 1}^{n − 1} (−3k + 1) \\ &= 2 + (−3) \cdot \frac{(n − 1)n}{2} + 1 \cdot (n − 1) \\ &= 2 − \frac{3}{2} n^2 + \frac{3}{2} n + n − 1 \\ &= −\frac{3}{2} n^2 + \frac{5}{2} n + 1 \end{align}\)
\(\displaystyle a_1 = −\frac{3}{2} + \frac{5}{2} + 1 = 2\) より、
\(n = 1\) のときも成り立つ。
答え: \(\color{red}{\displaystyle a_n = −\frac{3}{2} n^2 + \frac{5}{2} n + 1}\)
特殊解型 \(a_{n + 1} = pa_n + q\)
特殊解型は他パターンを解く過程でもよく出てくるので、基本 \(3\) 型と同じくらい重要です。
漸化式 \(a_{n + 1} = pa_n + q\)
→ \(a_{n + 1} − \alpha = p(a_n − \alpha)\) に変形する!
(式変形には特性方程式 \(\alpha = p\alpha + q\) を利用)
そうすることで、「等比型」の数列に帰着できます。

\(a_1 = −2\), \(4a_{n + 1} = 5a_n + 4\) を満たす数列 \(\{a_n\}\) の一般項を求めよ。
\(a_{n + 1}\) にかかっている係数で式全体を割れば、特殊解型ですね。
\(4a_{n + 1} = 5a_n + 4\) …①
① の両辺を \(4\) で割ると
\(\displaystyle a_{n + 1} = \frac{5}{4} a_n + 1\) …②
特性方程式 \(\displaystyle \alpha = \frac{5}{4} \alpha + 1\) …③ を解くと
\(\displaystyle −\frac{1}{4} \alpha = 1\)
\(\alpha = −4\)
② − ③より
\(\begin{array}{rr}& \displaystyle a_{n + 1} = \frac{5}{4} a_n + 1 \\−) & \displaystyle \alpha = \frac{5}{4} \alpha + 1 \\ \hline & \displaystyle a_{n + 1} − \alpha = \frac{5}{4} (a_n − \alpha)\end{array}\)
よって①は
\(\displaystyle a_{n + 1} + 4 = \frac{5}{4} (a_n + 4)\)
と変形できる。
ここで、数列 \(\{a_n + 4\}\) は初項 \(a_1 + 4 = 2\)、公比 \(\displaystyle \frac{5}{4}\) の等比数列であるから、
\(\displaystyle a_n + 4 = 2 \left( \frac{5}{4} \right)^{n − 1}\)
したがって、数列 \(\{a_n\}\) の一般項は
\(\displaystyle a_n = 2 \left( \frac{5}{4} \right)^{n − 1} − 4\)
答え: \(\color{red}{\displaystyle a_n = 2 \left( \frac{5}{4} \right)^{n − 1} − 4}\)
特性方程式は元の漸化式の \(a_{n + 1}\) や \(a_n\) を \(\alpha\) に置き換えた式、と習った人が多いかもしれません。
ただし、これは結果論に過ぎません。
特性方程式は本来、ゴールの漸化式と元の漸化式から変数(\(a_{n + 1}\) や \(a_n\))を消去して得られるものです。
\(n\) 次式型 \(a_{n + 1} = pa_n + f(n)\)
後ろに定数ではなく、\(n\) の多項式 \(f(n)\) が足されたパターンです。
この \(n\) 次式型も、特殊解型のように式変形すれば「等比型」の数列に帰着できます。
漸化式 \(a_{n + 1} = pa_n + f(n)\)
→ \(a_{n + 1} + g(n + 1) = p(a_n + g(n))\) に変形する!
(式変形には係数 \(\alpha, \beta\) などを利用)
\(n\) の多項式を、左辺(\(n + 1\) の式)と右辺(\(n\) の式)に分配するイメージです。
この考え方は、特性方程式を使うのとまったく同じです。

なお、\(f(n)\) が一次式の場合は「階差型」の数列を利用した解き方もあります。

\(a_1 = 2\), \(a_{n + 1} = 2a_n − 2n + 1\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
等比型に変形するやり方は次の通りです。
\(a_{n + 1} = 2a_n − 2n + 1\) …①
を
\(a_{n + 1} + \alpha(n + 1) + \beta = 2(a_n + \alpha n + \beta)\)
…② と変形する。
②を展開して
\(a_{n + 1} + \alpha n + \alpha + \beta = 2a_n + 2\alpha n + 2\beta\)
\(a_{n + 1} = 2a_n + 2\alpha n + 2\beta − \alpha n − \alpha − \beta\)
\(a_{n + 1} = 2a_n + \alpha n − \alpha + \beta\)
①と係数を比較して
\(\alpha = −2\)
\(−\alpha + \beta = 1\)
よって \(\alpha = −2\), \(\beta = −1\)
②から
\(a_{n + 1} − 2(n + 1) − 1 = 2(a_n − 2n − 1)\)
数列 \(\{a_n − 2n − 1\}\) は、初項 \(a_1 − 2 − 1 = −1\)、公比 \(2\) の等比数列であるから
\(a_n − 2n − 1 = −2^{n − 1}\)
よって
\(a_n = −2^{n − 1} + 2n + 1\)
答え: \(\color{red}{a_n = −2^{n − 1} + 2n + 1}\)
階差型を利用するやり方は次の通りです。
\(a_{n + 1} = 2a_n − 2n + 1\) …① より、
\(a_{n + 2} = 2a_{n + 1} − 2(n + 1) + 1\) …②
② − ①より
\(a_{n + 2} − a_{n + 1} = 2(a_{n + 1} − a_n) − 2\)
\(a_{n + 1} − a_n = b_n\) とおくと、
\(b_{n + 1} = 2b_n − 2\)
ここで、\(\alpha = 2\alpha − 2\) とおくと
\(\alpha = 2\) であるから、
\(b_{n + 1} − 2 = 2(b_n − 2)\)
と変形できる。
また、
\(\begin{align} b_1 &= a_2 − a_1 \\ &= (4 − 2 + 1) − 2 \\ &= 1 \end{align}\)
数列 \(\{b_n − 2\}\) は、
初項 \(b_1 − 2 = 1 − 2 = −1\)、公比 \(2\) の等比数列であるから
\(b_n − 2 = − 2^{n − 1}\)
よって
\(b_n = −2^{n − 1} + 2\)
\(a_{n + 1} − a_n = −2^{n − 1} + 2\)
①を代入して \(a_{n + 1}\) を削除すると
\(2a_n − 2n + 1 − a_n = −2^{n − 1} + 2\)
したがって
\(a_n = −2^{n − 1} + 2n + 1\)
答え: \(\color{red}{a_n = −2^{n − 1} + 2n + 1}\)
階比型 \(a_{n + 1} = f(n)a_n\)
\(a_n\) に \(n\) の多項式 \(f(n)\) がかかっているパターンです。
漸化式 \(a_{n + 1} = f(n)a_n\)
→ 両辺の \(n\) 番号が合うように変形する!
\(a_{n + 1}\) と \(a_n\) の係数の \(n\) 番号がそろうと、「等比型」の数列に帰着できます。

また、後ろに定数がくっついていても方針は変わりません。

なお、漸化式を \(a_1\) まで繰り返し使う解き方もあります(ただし、定数項がない場合のみ)。

\(a_1 = 2\), \(3na_{n + 1} = (n + 1)a_n\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
等比型に変形するやり方は次の通りです。
両辺を \(n(n + 1)\) で割ると
\(\displaystyle \frac{3a_{n + 1}}{n + 1} = \frac{a_n}{n}\)
\(\displaystyle \frac{a_n}{n} = b_n\) とおくと
\(3b_{n + 1} = b_n\)
\(\displaystyle b_{n + 1} = \frac{1}{3} b_n\)
数列 \(\{b_n\}\) は、初項 \(\displaystyle b_1 = \frac{a_1}{1} = 2\)、公比 \(\displaystyle \frac{1}{3}\) の等比数列であるから
\(\displaystyle b_n = 2 \left( \frac{1}{3} \right)^{n − 1} = \frac{2}{3^{n − 1}}\)
よって、
\(\displaystyle a_n = nb_n = \frac{2n}{3^{n − 1}}\)
答え: \(\color{red}{\displaystyle a_n = \frac{2n}{3^{n − 1}}}\)
漸化式を \(a_1\) まで繰り返し使うやり方は次の通りです。
両辺を \(3n\) で割ると
\(\displaystyle a_{n + 1} = \frac{n + 1}{3n} a_n\)
\(n \geq 2\) のとき
\(a_n\)
\(\displaystyle= \frac{n}{3(n − 1)} a_{n − 1}\)
\(\displaystyle = \frac{n}{3(n − 1)} \cdot \frac{n − 1}{3(n − 2)} a_{n − 2}\)
\(\displaystyle = \frac{n}{3(n − 1)} \cdot \frac{n − 1}{3(n − 2)} \cdot \frac{n − 2}{3(n − 3)} a_{n − 3}\)
\(\displaystyle = \frac{n}{3(n − 1)} \cdot \frac{n − 1}{3(n − 2)} \cdot \frac{n − 2}{3(n − 3)} \cdots \frac{2}{3} \cdot a_1\)
\(\displaystyle = \frac{n}{3^{n − 1}} \cdot a_1\)
\(\displaystyle = \frac{2n}{3^{n − 1}}\)
\(\displaystyle a_1 = \frac{2 \cdot 1}{3^{1 − 1}} = 2\) より、
\(n = 1\) のときも成り立つ。
よって、
\(\displaystyle a_n = \frac{2n}{3^{n − 1}}\)
答え: \(\color{red}{\displaystyle a_n = \frac{2n}{3^{n − 1}}}\)
指数型 \(a_{n + 1} = pa_n + q \cdot r^n\)
後ろに \(n\) を含む指数が足されたパターンです。
漸化式 \(a_{n + 1} = pa_n + q \cdot r^n\)
→ 両辺を \(r^{n + 1}\) で割る or かける!
\(a_{n + 1}\) と \(a_n\) の係数の \(n\) 番号がそろうと、別の数列と見ることができます。

\(a_1 = 2\), \(a_{n + 1} = 2a_n + 2^{n + 1}\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
両辺を \(2^{n + 1}\) で割ると
\(\displaystyle \frac{a_{n + 1}}{2^{n + 1}} = \frac{a_n}{2^n} + 1\)
\(\displaystyle \frac{a_n}{2^n} = b_n\) とおくと、
\(b_{n + 1} = b_n + 1\)
数列 \(\{b_n\}\) は、初項 \(\displaystyle b_1 = \frac{a_1}{2} = 1\)、公差 \(1\) の等差数列であるから
\(b_n = 1 + (n − 1)\cdot 1 = n\)
よって、
\(a_n = 2^n b_n = 2^n n\)
答え: \(\color{red}{a_n = 2^n n}\)
対数型 \(a_{n + 1} = pa_n^q\)
\(a_n\) に指数がかかっているパターンです。
漸化式 \(a_{n + 1} = pa_n^q\)
→ 両辺の対数をとる!
(底は \(a_1\) または \(p\))
対数をとることで、\(a_n\) にかかった指数が解消でき、「特殊解型」の数列に帰着します。

次のような場合も、対数をとるのが有効です。
- 二項の積 \(a_na_{n + 1}\) を含む漸化式
(項が分離できるため) - 累乗根 \(\sqrt[p]{a_n}\) を含む漸化式
(指数と同様に扱えるため)
\(\sqrt[p]{a_n} = a_n^{1/p}\)
\(a_1 = 1\), \(a_{n + 1} = 2a_n^2\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
\(a_1 = 1\), \(a_{n + 1} = 2a_n^2\) より、
すべての自然数 \(n\) について \(a_n > 0\)
漸化式の両辺の対数(底 \(2\))をとると
\(\begin{align} \log_2 a_{n + 1} &= \log_2 2a_n^2 \\ &= \log_2 2 + 2\log_2 a_n \\ &= 2\log_2 a_n + 1 \end{align}\)
ここで、\(\log_2 a_n = b_n\) とおくと
\(b_{n + 1} = 2b_n + 1\)
ここで、 \(\alpha = 2\alpha + 1\) とおくと
\(\alpha = −1\) であるから、
\(b_{n + 1} + 1 = 2(b_n + 1)\)
と変形できる。
数列 \(\{b_n + 1\}\) は
初項 \(b_1 + 1 = \log_2 a_1 + 1 = 0 + 1 = 1\)、
公比 \(2\) の等比数列であるから
\(b_n + 1 = 2^{n − 1}\)
\(b_n = 2^{n − 1} − 1\)
よって
\(\log_2 a_n = 2^{n − 1} − 1\)
したがって
\(a_n = 2^{2^{n − 1} − 1}\)
答え: \(\color{red}{a_n = 2^{2^{n − 1} − 1}}\)
逆数型 \(\displaystyle a_{n + 1} = \frac{pa_n}{qa_n + r}\)
右辺が \(a_n\) を含む分数で、特に分子が \(a_n\) の項だけのパターンです。
漸化式 \(\displaystyle a_{n + 1} = \frac{pa_n}{qa_n + r}\)
→ 両辺の逆数をとる!
逆数をとることで、右辺が \(a_n\) の項と定数に分離でき、別の数列と見ることができます。

\(\displaystyle a_1 = \frac{1}{4}\), \(\displaystyle a_{n + 1} = \frac{a_n}{3a_n + 1}\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
両辺の逆数をとると
\(\begin{align} \frac{1}{a_{n + 1}} &= \frac{3a_n + 1}{a_n} \\ &= 3 + \frac{1}{a_n} \end{align}\)
\(\displaystyle \frac{1}{a_n} = b_n\) とおくと
\(b_{n + 1} = b_n + 3\)
数列 \(\{b_n\}\) は、初項 \(\displaystyle b_1 = \frac{1}{a_1} = 4\)、公差 \(3\) の等差数列であるから
\(\begin{align} b_n &= 4 + (n − 1)\cdot 3 \\ &= 3n + 1 \end{align}\)
よって
\(\displaystyle a_n = \frac{1}{b_n} = \frac{1}{3n + 1}\)
答え: \(\color{red}{\displaystyle a_n = \frac{1}{3n + 1}}\)
一次分数型 \(\displaystyle a_{n + 1} = \frac{pa_n + q}{ra_n + s}\)
右辺が \(a_n\) の一次式でできた分数になっているパターンです。
逆数型と似ていますが、解き方はかなり複雑で、難易度が高めです。
漸化式 \(\displaystyle a_{n + 1} = \frac{pa_n + q}{ra_n + s}\)
→ 特性方程式 \(\displaystyle \alpha = \frac{p\alpha + q}{r\alpha + s}\) を解き、次のように置き換える。
(i) 異なる \(2\) 解 \(\alpha_1, \alpha_2\) をもつ場合
→ \(\displaystyle b_n = \frac{a_n − \alpha_1}{a_n − \alpha_2}\) とおく
(ii) 重解 \(\alpha\) をもつ場合
→ \(b_n = a_n − \alpha\) とおく
\(b_{n + 1}\) を計算していくと、数列 \(\{b_n\}\) のパターンが見えてきます。

\(a_1 = 3\), \(\displaystyle a_{n + 1} = \frac{4a_n + 3}{a_n + 6}\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
特性方程式
\(\displaystyle \alpha = \frac{4\alpha + 3}{\alpha + 6}\) を解くと、
\(\alpha^2 + 6\alpha = 4\alpha + 3\)
\(\alpha^2 + 2\alpha − 3 = 0\)
\((\alpha − 1)(\alpha + 3) = 0\)
\(\alpha = 1, −3\)
ここで、\(\displaystyle b_n = \frac{a_n − 1}{a_n + 3}\) とおくと
\(\begin{align}\displaystyle b_{n + 1} &= \frac{a_{n + 1} − 1}{a_{n + 1} + 3}\\&= \frac{\frac{4a_n + 3}{a_n + 6} − 1}{\frac{4a_n + 3}{a_n + 6} + 3}\\& = \frac{\frac{(4a_n + 3) − (a_n + 6)}{a_n + 6}}{\frac{(4a_n + 3) + 3(a_n + 6)}{a_n + 6}}\\& = \frac{3a_n − 3}{7a_n + 21}\\& = \frac{3(a_n − 1)}{7(a_n + 3)}\\& = \frac{3}{7} b_n\end{align}\)
よって、数列 \(\{b_n\}\) は初項 \(\displaystyle b_1 = \frac{3 − 1}{3 + 3} = \frac{1}{3}\)、公比 \(\displaystyle \frac{3}{7}\) の等比数列であるから
\(\displaystyle b_n = \frac{1}{3} \left( \frac{3}{7} \right)^{n − 1}\)
\(\displaystyle b_n = \frac{a_n − 1}{a_n + 3}\) を \(a_n\) について整理して
\(b_na_n + 3b_n = a_n − 1\)
\((b_n − 1)a_n = −(3b_n + 1)\)
\(\displaystyle a_n = −\frac{3b_n + 1}{b_n − 1}\)
よって
\(\begin{align}\displaystyle a_n &= −\frac{\left( \frac{3}{7} \right)^{n − 1} + 1}{\frac{1}{3} \left( \frac{3}{7} \right)^{n − 1} − 1}\\& = −3 \cdot \frac{\left( \frac{3}{7} \right)^{n − 1} + 1}{\left( \frac{3}{7} \right)^{n − 1} − 3}\end{align}\)
分母、分子に \(7^{n − 1}\) をかけて
\(\begin{align}\displaystyle a_n &= −3 \cdot \frac{3^{n − 1} + 7^{n − 1}}{3^{n − 1} − 3 \cdot 7^{n − 1}}\\&= 3 \cdot \frac{7^{n − 1} + 3^{n − 1}}{3 \cdot 7^{n − 1} − 3^{n − 1}}\\&= \frac{7^{n − 1} + 3^{n − 1}}{7^{n − 1} − 3^{n − 2}}\end{align}\)
答え: \(\color{red}{\displaystyle a_n = \frac{7^{n − 1} + 3^{n − 1}}{7^{n − 1} − 3^{n − 2}}}\)
隣接三項間漸化式の解き方
隣接三項間漸化式の解き方を説明します。
定数が \(0\) のパターンと \(0\) 以外のパターンがありますが、アプローチはどちらも一緒です。
漸化式 \(a_{n + 2} + pa_{n + 1} + qa_n = r\)
→ 特性方程式 \(x^2 + px + q = 0\) を解き、解の個数に応じて式変形する!
上記の特性方程式は、
\(a_{n + 2} + pa_{n + 1} + qa_n = r\)
を
\(a_{n + 2} \color{skyblue}{− \alpha} a_{n + 1} = \color{orange}{\beta}(a_{n + 1} \color{skyblue}{− \alpha} a_n) + r\)
の形に変形する過程で現れます。
( \(\color{skyblue}{\alpha}, \color{orange}{\beta}\) は \(x^2 + px + q = 0\) の解となる)
式変形の進め方は、定数 \(r\) が \(0\) かそうでないか、特性方程式の解の個数によって異なりますが、基本方針は同じです。
\(a_{n + 2} + pa_{n + 1} + qa_n = 0\)(定数が \(0\))
等比型の数列を経由して、目的の数列を求めます。

\(a_1 = 3\), \(a_2 = 10\), \(a_{n + 2} = a_{n + 1} + 12a_n\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
\(a_{n + 2} − a_{n + 1} − 12a_n = 0\) …①
特性方程式 \(x^2 − x − 12 = 0\) を解くと
\((x − 4)(x + 3) = 0\)
\(x = 4, −3\)
よって①は
\(\left\{\begin{array}{l}a_{n + 2} − 4a_{n + 1} = −3(a_{n + 1} − 4a_n) \text{ …②}\\a_{n + 2} + 3a_{n + 1} = 4(a_{n + 1} + 3a_n)\text{ …③}\end{array}\right.\)
と変形できる。
②より、数列 \(\{a_{n + 1} − 4a_n\}\) は
初項 \(a_2 − 4a_1 = −2\)、公比 \(−3\) の等比数列であるから
\(a_{n + 1} − 4a_n = −2(−3)^{n − 1}\) …②’
③より、数列 \(\{a_{n + 1} + 3a_n\}\) は
初項 \(a_2 + 3a_1 = 19\)、公比 \(4\) の等比数列であるから
\(a_{n + 1} + 3a_n = 19 \cdot 4^{n − 1}\) …③’
③’ − ②’ より、
\(7a_n = 19 \cdot 4^{n − 1} + 2(−3)^{n − 1}\)
よって
\(\displaystyle a_n = \frac{1}{7} \{19 \cdot 4^{n − 1} + 2(−3)^{n − 1}\}\)
答え: \(\color{red}{\displaystyle a_n = \frac{1}{7} \{19 \cdot 4^{n − 1} + 2(−3)^{n − 1}\}}\)
複雑な漸化式の場合、得られる一般項も複雑になります。
不安なときは、得られた一般項に \(n = 1, 2\) などを代入し、検算してみましょう。
\(a_{n + 2} + pa_{n + 1} + qa_n = r\)(定数が \(0\) 以外)
解の個数によって異なる型の数列を経由して、目的の数列を求めます。

\(a_1 = 1\), \(a_2 = 2\), \(a_{n + 2} = 2a_{n + 1} − a_n + 5\) で定められる数列 \(\{a_n\}\) の一般項を求めよ。
\(a_{n + 2} = 2a_{n + 1} − a_n + 5\) …①
特性方程式 \(x^2 = 2x − 1\) を解くと
\(x^2 − 2x + 1 = 0\)
\((x − 1)^2 = 0\)
\(x = 1\)
よって①は
\(a_{n + 2} − a_{n + 1} = a_{n + 1} − a_n + 5\)
と変形できる。
ここで、数列 \(\{a_{n + 1} − a_n\}\) は
初項 \(a_2 − a_1 = 2 − 1 = 1\)、公差 \(5\) の等比数列であるから
\(\begin{align}a_{n + 1} − a_n &= 1 + (n − 1)5 \\&= 5n − 4\end{align}\)
すなわち
\(a_{n + 1} = a_n + 5n − 4\)
よって、数列 \(\{a_n\}\) は一般項が \(5n − 4\) の階差数列をもつ。
\(n \geq 2\) のとき
\(\begin{align} a_n &= a_1 + \sum_{k = 1}^{n − 1} (5k − 4) \\ &= 1 + 5 \cdot \frac{(n − 1)n}{2} − 4(n − 1) \\ &= 1 + \frac{5}{2} n^2 − \frac{5}{2} n − 4n + 4 \\ &= \frac{5}{2} n^2 − \frac{13}{2} n + 5 \end{align}\)
\(\begin{align}a_1 &= \frac{5}{2} \cdot 1^2 − \frac{13}{2} \cdot 1 + 5 \\&= \frac{5 − 13 + 10}{2} \\&= 1\end{align}\)
より、\(n = 1\) のときも成り立つ。
よって
\(\displaystyle a_n = \frac{5}{2} n^2 − \frac{13}{2} n + 5\)
答え: \(\color{red}{\displaystyle a_n = \frac{5}{2} n^2 − \frac{13}{2} n + 5}\)
以上が漸化式全 12 パターンの解き方まとめでした!
各パターンのとっかかりをつかんだら、あとはとにかく練習あるのみです。
たくさんの問題を解いて漸化式をマスターしてくださいね!
