この記事では、「オイラーの公式」および、最も美しい数式として有名な「オイラーの等式」について紹介していきます。
公式の証明などもできるだけわかりやすく説明していきますので、ぜひこの記事を通して知識を深めてくださいね！
目次
オイラーの公式とは？
オイラーの公式とは、複素指数関数と三角関数との間に成り立つ以下の公式です。
任意の偏角 \(\theta\) について、
\begin{align}\color{red}{e^{i\theta} = \cos\theta + i\sin\theta}\end{align}
特に \(\theta\) が実数の場合、\(e^{i\theta}\) は複素数平面上で \(\theta\) を偏角とする複素数に対応します。
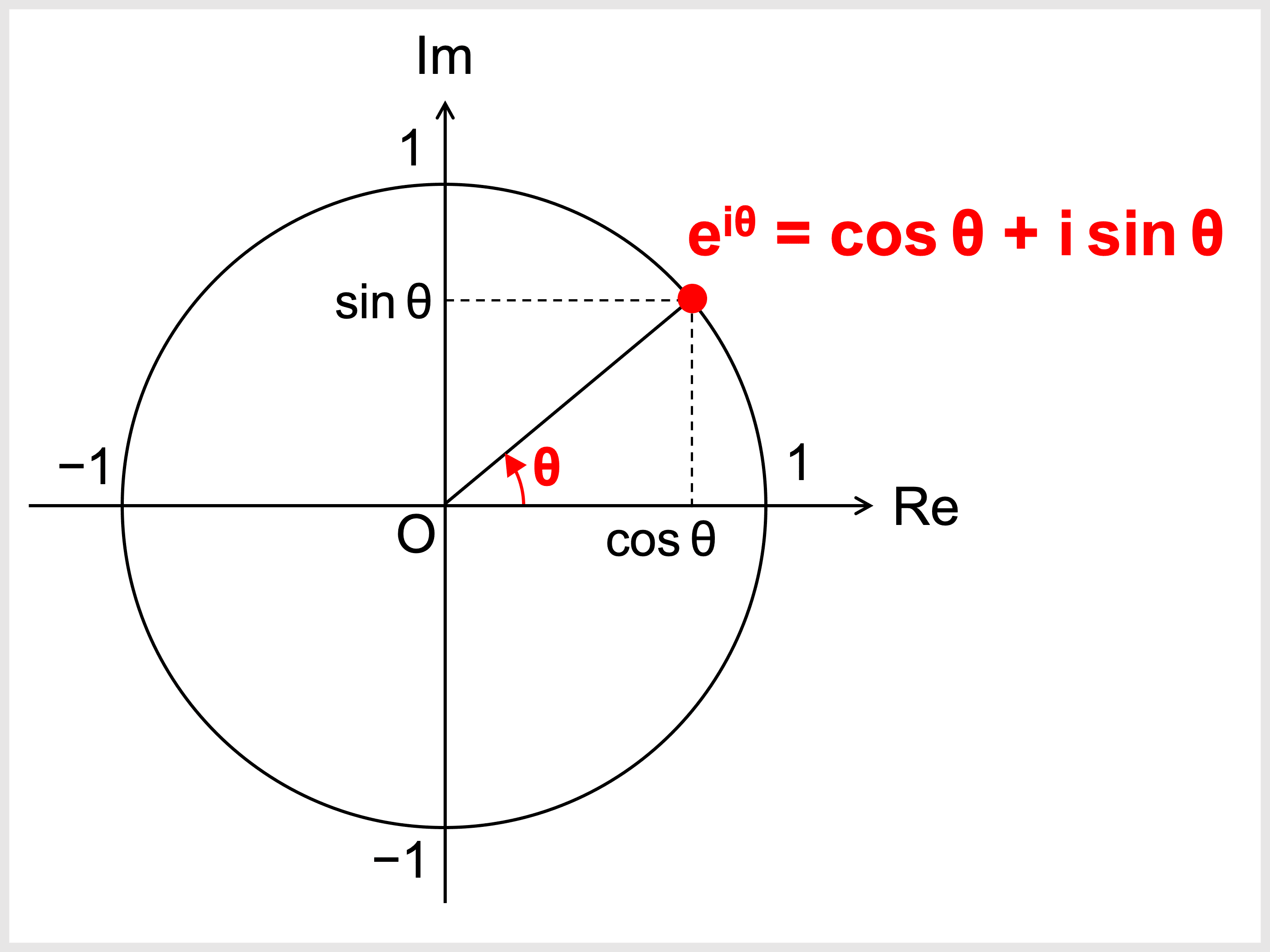
この公式は、純粋数学のさまざまな分野、また電気工学・物理学などの解析手法としてとても重要です。
物理学者リチャード・ファインマンが「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」だと述べたことが有名です。
オイラーの等式とは？
オイラーの公式において、\(\theta = \pi\) を代入した式をオイラーの等式といいます。
オイラーの公式 \(e^{i\theta} = \cos\theta + i\sin\theta\) において、\(\theta = \pi\) のとき
\begin{align}e^{i\pi} = −1 + 0\end{align}
すなわち
\begin{align}\color{red}{e^{i\pi} + 1 = 0}\end{align}
オイラーの等式の美しさ
オイラーの等式は、
- 解析学で定義されたネイピア数 \(e\)
- 代数学で定義された虚数単位 \(i\)
- 幾何学で定義された円周率 \(\pi\)
また、
- 乗法単位元 \(1\)（何にかけても数が変わらない数）
- 加法単位元 \(0\)（何に足しても数が変わらない数）
を含むこと、そしてそれら以外を含まない非常にシンプルな式であることから、数学史上最も美しい等式と言われています。
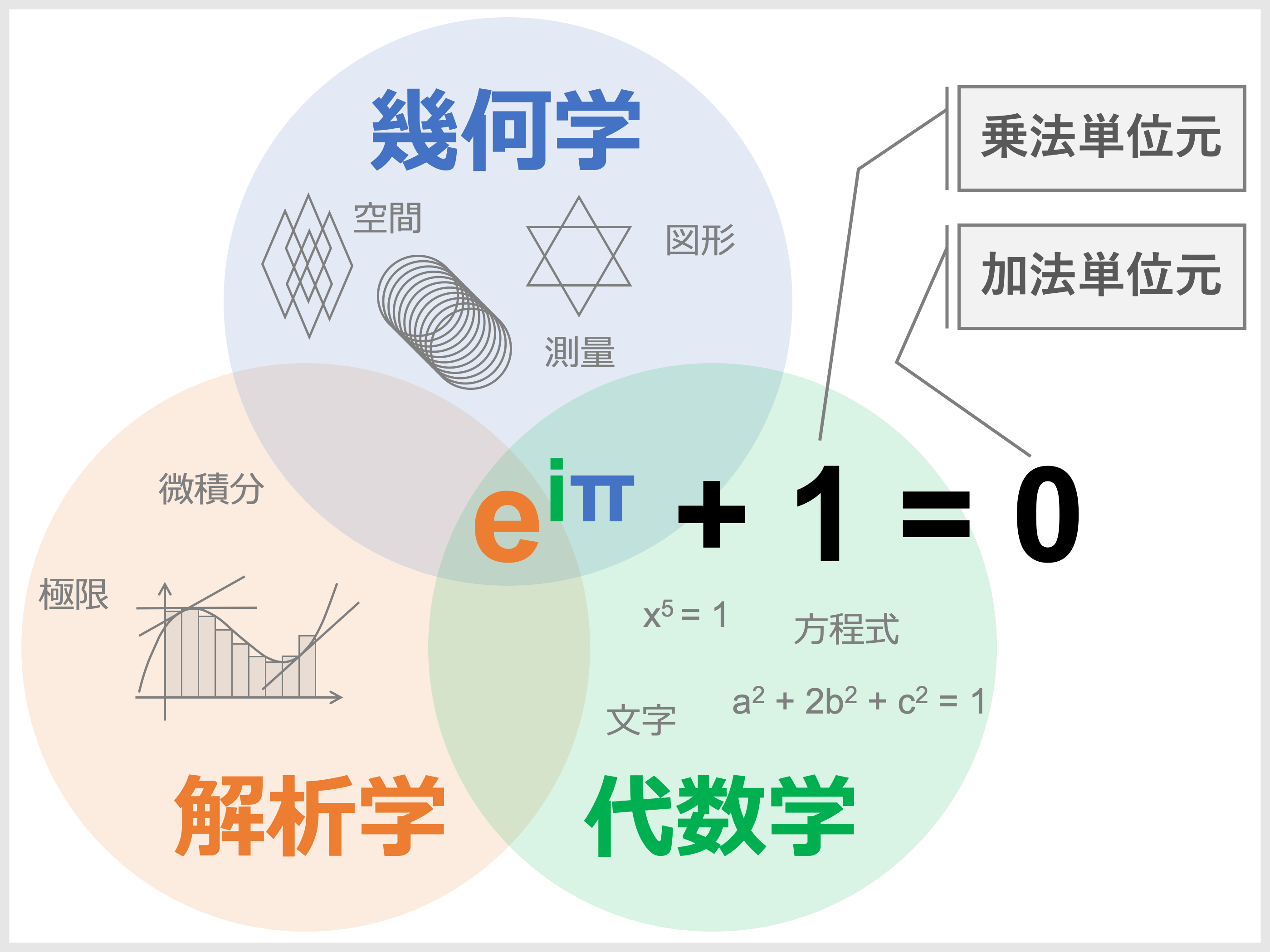
まったく別々の経緯で定義された \(3\) つの数 \(e\), \(i\), \(\pi\) が、たった \(1\) つの単純な式で結びつくのがなんとも神秘的ですね。
「ネイピア数 \(e\)」「虚数単位 \(i\)」「円周率 \(\pi\)」については、個別の記事で詳しく説明しています。
- ネイピア数 \(e\)
自然対数 ln、自然対数の底 e とは？定義や微分積分公式 - 虚数単位 \(i\)
複素数とは？公式や i の 2 乗の意味、計算問題の解き方 - 円周率 \(\pi\)
円周率 π とは？求め方や100桁までの覚え方を紹介！
オイラーの公式の証明
ここでは、マクローリン展開を利用してオイラーの公式を示す方法を簡単に説明します。
「マクローリン展開」とは、ある関数 \(f(x)\) を無限次の多項式で表したもののうち、\(x = 0\) における情報をもとにしたものです。
近似値・近似式とは？公式や求め方、テイラー展開・マクローリン展開も！
すべての実数 \(x\) に対して、\(e^x\), \(\sin x\), \(\cos x\) をマクローリン展開すると、
\(\displaystyle e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots\) …①
\(\displaystyle \sin x = x − \frac{x^3}{3!} + \frac{x^5}{5!} − \frac{x^7}{7!} + \cdots\) …②
\(\displaystyle \cos x = 1 − \frac{x^2}{2!} + \frac{x^4}{4!} − \frac{x^6}{6!} + \cdots\) …③
①の \(x\) を \(ix\) に置き換えると、\(i^2 = −1\) より
\(\displaystyle e^{ix} = 1 + ix − \frac{x^2}{2!} − \frac{ix^3}{3!} + \frac{x^4}{4!} + \cdots\) …④
実部と虚部に分けると、
\(\displaystyle e^{ix} = \left( 1 − \frac{x^2}{2!} + \frac{x^4}{4!} − \cdots \right) \) \(\displaystyle + \,i \left( x − \frac{x^3}{3!} + \frac{x^5}{5!} − \cdots \right)\)
②、③より
\(e^{ix} = \cos x + i\sin x\) …⑤
（証明終わり）
虚数のべき乗 \(e^{ix}\) を勝手に実数のべき乗と同じように計算してしまっていいのか？という問題はあるものの、この公式自体を \(e^{ix}\) の定義と見ることもできます。
試しに、実数のべき乗と同様に「\((e^{ix})’ = ie^{ix}\)」が成り立つと仮定して、④、⑤を微分してみると、
\(\displaystyle (e^{ix})’\)
\(\displaystyle = \left( 1 + ix − \frac{x^2}{2!} − \frac{ix^3}{3!} + \frac{x^4}{4!} +\cdots \right)’\)
\(\displaystyle = 0 + i − x − \frac{ix^2}{2!} + \frac{x^3}{3!} + \cdots\)
\(\displaystyle = i \left( 1 + ix − \frac{x^2}{2!} − \frac{ix^3}{3!} + \cdots \right)\)
\(= ie^{ix}\)
\(\begin{align} (e^{ix})’ &= (\cos x + i\sin x)’ \\ &= −\sin x + i\cos x \\ &= i(\cos x + i\sin x) \\ &= ie^{ix} \end{align}\)
このように、両者が一致しました。
また、指数関数 \(f(x) = e^x\) の重要な特徴、「\(f(0) = 1\)」が成り立つかも試してみましょう。
\(\begin{align} e^{i \cdot 0} &= e^0 \\ &= 1 \end{align}\)
④では
\(\begin{align} e^{i \cdot 0} &= 1 + 0 − 0 − 0 + \cdots \\ &= 1 \end{align}\)
⑤では
\(\begin{align} e^{i \cdot 0} &= \cos 0 + i\sin 0 \\ &= 1 + 0 \\ &= 1 \end{align}\)
こちらも、すべて成り立ちましたね。
これらのことも、オイラーの公式の正しさの根拠になっています。
オイラーの公式の使い方
高校数学では習わないオイラーの公式ですが、知っていると役に立つ場面もあります。
ここでは、オイラーの公式の活用方法をいくつか紹介します。
極形式の複素数同士の計算を楽にできる
オイラーの公式から、複素数の極形式 \(z = |z|(\cos \theta + i \sin \theta)\) は \(z = |z|e^{i\theta}\) に等しいといえます。
したがって、三角関数の加法定理の計算を指数関数の積の計算に変換できます。
（例）複素数の積 \(z_1z_2\)
\(z_1 = |z_1|(\cos\theta_1 + i\sin\theta_1)\)
\(z_2 = |z_2|(\cos\theta_2 + i\sin\theta_2)\)
とする。
【極形式で計算（三角関数）】
（見切れる場合は横へスクロール）
\(z_1z_2\)
\(= |z_1||z_2|(\cos \theta_1 + i\sin \theta_1)(\cos \theta_2 + i\sin \theta_2)\)
\(= |z_1||z_2|\{\cos \theta_1\cos \theta_2 − \sin \theta_1\sin \theta_2 + i(\sin \theta_1\cos \theta_2 + \cos \theta_1\sin \theta_2)\}\)
\(= |z_1||z_2|\{\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)\}\)
（加法定理を利用）
【指数関数に変換して計算】
オイラーの公式より
\(z_1 = |z_1|e^{i\theta_1}\)
\(z_2 = |z_2|e^{i\theta_2}\)
であるから、
\(z_1z_2\)
\(= |z_1|e^{i\theta_1} \cdot |z_2|e^{i\theta_2}\)
\(= |z_1||z_2|e^{i(\theta_1 + \theta_2)}\)
\(= |z_1||z_2|\{\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)\}\)
複素数同士の積で偏角が足し算されるのには、指数関数の性質が関わっていることがよくわかりますね（\(e^{km} \cdot e^{kn} = e^{k(m+n)}\)）。
「複素数の計算」については、以下の記事で詳しく説明しています。
複素数平面を総まとめ！数IIIで習う性質・公式一覧
ドモアブルの定理を簡単に導ける
オイラーの公式の両辺を \(n\) 乗すると、ドモアブルの定理が導かれます。
\(e^{i\theta} = \cos \theta + i\sin \theta\) の両辺を \(n\) 乗して
\(e^{in\theta} = (\cos \theta + i\sin \theta)^n\)
ここで、左辺はオイラーの公式の左辺で \(\theta\) を \(n\theta\) に置き換えたものに等しいから、
\(\color{red}{(\cos \theta + i\sin \theta)^n = \cos n\theta + i\sin n\theta}\)
（ドモアブルの定理）
「ドモアブルの定理」については、以下の記事で詳しく説明しています。
ドモアブルの定理とは？意味や証明、問題の解き方
（おまけ）三角関数を指数関数で表せる
オイラーの公式とその共役複素数から、三角関数を指数関数だけで表すことができます。
オイラーの公式
\(e^{i\theta} = \cos \theta + i\sin \theta\) …①
の共役複素数をとると
\(e^{−i\theta} = \cos \theta − i\sin \theta\) …②
① + ② より
\(e^{i\theta} + e^{−i\theta} = 2\cos \theta\)
\(2\) で割ると
\(\displaystyle \cos \theta = \frac{e^{i\theta} + e^{−i\theta}}{2}\)
① − ② より
\(e^{i\theta} − e^{−i\theta} = 2i\sin \theta\)
\(2i\) で割ると
\(\displaystyle \sin \theta = \frac{e^{i\theta} − e^{−i\theta}}{2i}\)
よって
\(\left\{\begin{array}{l} \displaystyle \cos \theta = \frac{e^{i\theta} + e^{−i\theta}}{2}\\ \displaystyle \sin \theta = \frac{e^{i\theta} − e^{−i\theta}}{2i}\end{array}\right.\)
この性質が高校レベルの問題で役に立つことはあまりありませんが、例えば三角関数の積分を指数関数の積分に置き換えるなどの利用方法があります。
以上で解説は終わりです。
シンプルながら、数学のさまざまな分野をつなぐとても奥深い数式です。
高校数学の範囲でも役立つ知識なので、ぜひ覚えておいてくださいね！