この記事では、「近似値」や「近似式」の意味や求め方をわかりやすく解説していきます。
また、大学レベルの知識であるテイラー展開やマクローリン展開についても少しだけ触れていきます。
有名な公式や計算問題なども説明していきますので、ぜひこの記事を通して理解を深めてくださいね。
目次
近似値とは?
近似値とは、真の値に近い値のことで、次のようなときに真の値の代わりに使用されます。
- 真の値を求めるのが難しい
「非常に複雑な関数について考えたい」「複数の要因が絡み合う物理現象を扱いたい」ときなど、限られたリソース(人の頭脳、コンピュータ)では正確な計算が難しい、とんでもなく時間がかかるといったことがあります。
そのようなときは、大筋の計算に影響が少ない部分は削ぎ落として、できるだけ簡単に、適度に正しい値(= 近似値)が求められればいいですよね。 - 計算を簡略化したい
真の値の区切りが悪く(無理数など)、切りのいい値にした方が目的の計算がしやすいときに用います。円周率を \(3.14\) という近似値で計算するのもまさにこのためですね(小学生に \(5 \times 5 \times 3.141592653\cdots\) を電卓なしで計算しなさいというのはなかなか酷ですから)。
また、近似値と真の値との差を「誤差」といいます。
\(\text{(誤差)} = \text{(近似値)} − \text{(真の値)}\)
近似値は、議論の是非に影響がない誤差の範囲内に収める必要があります。
数学や物理では、ある数がほかの数に比べて十分に小さく、無視しても差し支えないときに近似することがよくあります。
ある正の数 \(a\), \(b\) について、\(a\) が \(b\) よりも非常に小さいことを記号「\(\ll\)」を用いて
\begin{align}\color{red}{a \ll b}\end{align}
と表す。
また、左辺と右辺がほぼ等しいことは記号「\(\simeq\)」(または \(\approx\))を用いて表す。
(例)\(x\) を無視する近似
\begin{align}\color{red}{1 + x^2 \simeq 1 \,\, (|x| \ll 1)}\end{align}
記号「≒」(ニアリーイコール) は、切りの悪い数値を丸めるとき(四捨五入などの概算)に使用されます。
\(\pi \ (= 3.141592653\cdots) ≒ 3.14\)
海外では「≐」の方が一般的とされています。
また、概算の方法については以下の記事で説明しています。
 概数(がい数)とは?意味や計算問題(四捨五入など)の復習!
概数(がい数)とは?意味や計算問題(四捨五入など)の復習!
近似式とは?
ある関数 \(f(x)\) の値を正確に求めるのが難しいときに、ある程度近しい別の関数を用いて計算しやすくすることがあります。
このとき用いる別の関数を「近似式」または「近似関数」といいます。
関数の一次近似
関数の近似のうち、最もシンプルなのが「一次近似」です。
一次近似とは、関数 \(f(x)\) のある点周辺の値を一次関数(一次式)で近似する方法です。
ある点 \(\mathrm{A}\) に接線 \(\ell\) を引くと、少なくとも点 \(\mathrm{A}\) 周辺では \(f(x)\) の値を \(\ell\) の式で近似して求めることができそうですよね。
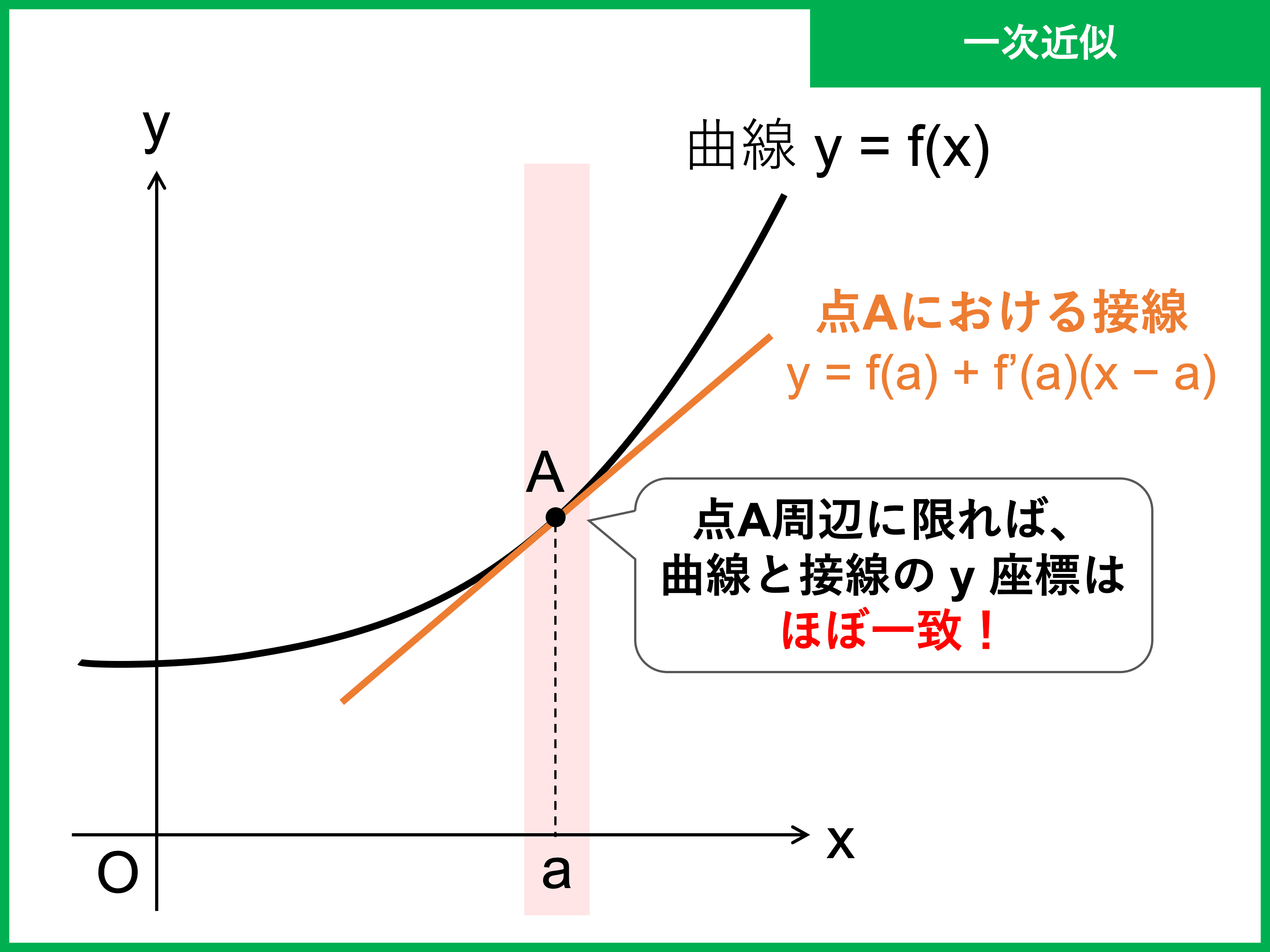
したがって、点 \(\mathrm{A}\) における接線の方程式が、点 \(\mathrm{A}\) 周辺での \(f(x)\) の一次近似式といえます。
以降示す公式は、すべて \(f(x)\) が \(x = a\) 付近で微分可能であることが前提です。
\(x \simeq a\) のとき、
\begin{align}\color{red}{f(x) \simeq f(a) + f’(a)(x − a)}\end{align}
特に、\(x\) が十分小さいとき(\(|x| \simeq 0\) のとき)、
\begin{align}\color{red}{f(x) \simeq f(0) + f’(0)x}\end{align}
また、微分係数 \(f’(a)\) の定義式から以下の近似式も導出できます。
関数 \(y = f(x)\) の微分係数 \(f’(a)\) は
\begin{align}\color{red}{\displaystyle \lim_{h \to 0} \frac{f(a + h) − f(a)}{h} = f’(a)}\end{align}
\(|h|\) が十分小さいとき(\(|h| \simeq 0\) のとき)
\begin{align}\color{red}{\displaystyle \frac{f(a + h) − f(a)}{h} \simeq f’(a)}\end{align}
すなわち
\begin{align}\color{red}{f(a + h) \simeq f(a) + f’(a)h} \text{…①}\end{align}
関数の多項式近似
近似関数の次数を一次、二次、三次…と上げていくと、近似の精度が高くなっていきます。
一般に、関数 \(f(x)\) のある点周辺の値を多項式で近似する方法を多項式近似といいます。
\(x \simeq a\) のとき、
\(\displaystyle f(x) \) \(\displaystyle \simeq f(a) + \frac{f’(a)}{1!} (x − a) + \frac{f’’(a)}{2!} (x − a)^2 \) \(\displaystyle +\, \frac{f’’’(a)}{3!} (x − a)^3 + \cdots \) \(\displaystyle+\, \frac{f^{(n)}(a)}{n!} (x − a)^n\)
特に、\(x\) が十分小さいとき (\(|x| \simeq 0\) のとき)、
\(\displaystyle f(x) \) \(\displaystyle \simeq f(0) \, + \frac{f’(0)}{1!} x + \frac{f’’(0)}{2!} x^2 \) \(\displaystyle +\, \frac{f’’’(0)}{3!} x^3 + \cdots + \frac{f^{(n)}(0)}{n!} x^n\)
\(f^{(n)}(x)\) は \(f(x)\) を \(n\) 回微分したもの(第 \(n\) 次導関数)です。
関数の級数展開(テイラー展開・マクローリン展開)
そして、多項式近似の次数を無限に大きくしたものを「テイラー展開」といいます。
\(x = a\) のとき、関数 \(f(x)\) が無限回微分可能であれば(※)、
\(f(x) \)
\(\displaystyle = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x − a)^n \)
\(\displaystyle = f(a) + \frac{f’(a)}{1!} (x − a) + \frac{f’’(a)}{2!} (x − a)^2 \) \(\displaystyle +\, \frac{f’’’(a)}{3!} (x − a)^3 + \cdots \) \(\displaystyle +\, \frac{f^{(n)}(a)}{n!} (x − a)^n + \cdots \)
特に、テイラー展開において \(a = 0\) とした場合を「マクローリン展開」といいます。
\(x = 0\) のとき、関数 \(f(x)\) が無限回微分可能であれば(※)、
\(f(x)\)
\(\displaystyle = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!} x^n \)
\(\displaystyle = f(0) + \frac{f’(0)}{1!} x + \frac{f’’(0)}{2!} x^2 \) \(\displaystyle +\, \frac{f’’’(0)}{3!} x^3 + \cdots + \frac{f^{(n)}(0)}{n!} x^n + \cdots \)
先ほどまでの多項式近似とは違って、左辺と右辺が「\(\simeq\)」ではなく「\(=\)」でつながった等式であることに注目してください。
これは、ある関数は無限次の多項式で(近似できるのではなく)表せることを意味しています。
※ テイラー展開・マクローリン展開は無限級数なので、等式が成り立つには満たされるべき収束条件があります。
厳密な説明はかなり難しくなってしまうので省略しますが、テイラー展開・マクローリン展開できない関数もあると理解しておきましょう。
なお、「無限級数」については以下の記事で詳しく説明しています。
 無限級数、無限等比級数とは?和の公式や求め方、図形問題
無限級数、無限等比級数とは?和の公式や求め方、図形問題
近似の有名公式
近似式の中で、特によく使用されるものをいくつか紹介します。
物理でよく用いられたり、難関大の入試で登場したりもするので、知っておいて損はないでしょう。
一次近似の有名公式
\(|x| \ll 1\) のとき、
- \(\displaystyle \sqrt{1 + x} \simeq 1 + \frac{x}{2}\)
- \((1 + x)^n \simeq 1 + nx\)
- \(\sin x \simeq x\)
- \(\cos x \simeq 1\)
- \(\tan x \simeq x\)
- \(e^x \simeq 1 + x\)
- \(\log(1 + x) \simeq x\)
多項式近似の有名公式
なお、いずれもマクローリン展開。
- \(\displaystyle (1 + x)^n \)
\(\displaystyle = 1 + nx + \frac{n(n − 1)}{2!} x^2 \,+ \) \(\displaystyle \frac{n(n − 1)(n − 2)}{3!} x^3 + \cdots\) - \(\displaystyle \sin x \)
\(\displaystyle = x − \frac{x^3}{3!} + \frac{x^5}{5!} − \cdots\)
\(\displaystyle = x − \frac{x^3}{6} + \frac{x^5}{120} − \cdots\) - \(\displaystyle \cos x \)
\(\displaystyle = 1 − \frac{x^2}{2!} + \frac{x^4}{4!} − \cdots\)
\(\displaystyle = 1 − \frac{x^2}{2} + \frac{x^4}{24} − \cdots\) - \(\displaystyle \tan x \)
\(\displaystyle = x − \frac{1}{3} x^3 + \frac{2}{15} x^5 − \cdots\) - \(\displaystyle e^x \)
\(\displaystyle = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots\)
\(\displaystyle = 1 + x + \frac{1}{2} x^2 + \frac{1}{6} x^3 + \cdots\) - \(\displaystyle \log(1 + x) \)
\(\displaystyle = x − \frac{1}{2} x^2 + \frac{1}{3} x^3 − \cdots\) \((−1 < x \leq 1)\)
多項式近似の次数とイメージ
テイラー展開・マクローリン展開の式において、具体的な \(n\) の値を代入すると多項式近似となります。
よく見ると、一次近似の式は \(n = 1\) を代入したものになっていますね。
関数において注目している点に非常に近いところであれば、\(n = 1\) でも近似としては十分役割を果たすのです。
当然、\(n = 2, 3, \cdots\) と次数を上げていけば、より広い範囲を近似できるようになっていきます。

ただし、基本的に近似できるのは注目している点 \((x = a)\) 付近の値だけ、と認識しておきましょう(関数によって、近似可能な範囲は異なります)。
近似値の求め方【計算問題】
ここでは、一次近似の考え方で近似式や近似値を求める問題を解いてみましょう。
計算問題①「\(\sqrt[4]{80}\) の近似値」
\(|x|\) が十分に小さいとき、\(f(x) = \sqrt[4]{1 + x}\) の近似式を作り、\(\sqrt[4]{80}\) の近似値を小数第 \(3\) 位を四捨五入して求めよ。

\(|x|\) が十分に小さいときは、一次近似の公式「\(f(x) \simeq f(0) + f’(0)x\)」が使えますね。
また、作った近似式に当てはめられるように、求めたい値をうまく変形しましょう。
\(\sqrt[4]{1 + x} = (1 + x)^{\frac{1}{4}}\) より、
\(\displaystyle f’(x) = \frac{1}{4} (1 + x)^{−\frac{3}{4}}\)
であるから、\(\displaystyle f’(0) = \frac{1}{4}\)
\(|x|\) が十分に小さいとき、
\(\displaystyle f(x) \simeq f(0) + f’(0)x = 1 + \frac{1}{4} x\)
また、
\(\begin{align} \sqrt[4]{80} &= \sqrt[4]{81 − 1} \\ &= \sqrt[4]{3^4 − 1} \\ &= 3 \cdot \sqrt[4]{1 − \frac{1}{81}} \end{align}\)
よって、
\(\begin{align} \sqrt[4]{80} &\simeq 3 \left\{ 1 + \frac{1}{4} \cdot \left( −\frac{1}{81} \right) \right\} \\ &= 3 \left( 1 − \frac{1}{324} \right) \\ &= 3 \cdot \frac{323}{324} \\ &= \frac{323}{108} \\ &= 2.990\cdots \\ &≒ 2.99 \end{align}\)
答え: \(\color{red}{\displaystyle f(x) \simeq 1 + \frac{1}{4} x}\), \(\color{red}{\sqrt[4]{80} ≒ 2.99}\)
計算問題②「\(\sin 59^\circ\) の近似値」
\(\sin 59^\circ\) の近似値を \(\pi = 3.142\), \(\sqrt{3} = 1.732\) として小数第 \(3\) 位まで求めよ。

三角関数の導関数は角が弧度法であることが前提なので、まずは度 (\({}^\circ\)) からラジアン (\(\mathrm{rad}\)) に直しましょう。
また、近似では「\(f(a + h) \simeq f(a) + f’(a)h\)(\(|h|\) が十分小さいとき)」を利用しましょう。
\(\begin{align} \sin 59^\circ &= \sin(60^\circ − 1^\circ) \\ &= \sin \left( \frac{\pi}{3} − \frac{\pi}{180} \right) \end{align}\)
\((\sin x)’ = \cos x\) より、\(|h|\) が十分小さいとき
\(\sin(a + h) \simeq \sin a + h\cos a\)
よって、
\(\begin{align} \sin 59^\circ &= \sin\left( \frac{\pi}{3} − \frac{\pi}{180} \right) \\ &\simeq \sin\frac{\pi}{3} + \left( −\frac{\pi}{180} \right) \cos\frac{\pi}{3} \\ &= \frac{\sqrt{3}}{2} − \frac{\pi}{180} \cdot \frac{1}{2} \\ &= \frac{180\sqrt{3} − \pi}{360} \\ &≒ \frac{180 \cdot 1.732 − 3.142}{360} \\ &= 0.8572\cdots \\ &≒ 0.857 \end{align}\)
答え: \(\color{red}{0.857}\)
以上で問題も終わりです。
だいたいどのくらいの値になるのかを、なるべく簡単に求める。近似の考え方は、いろいろなところで使われています。
数式そのものだけでなく、考え方の背景を理解することも心がけましょう!
