この記事では、「フィボナッチ数列」についてわかりやすく解説していきます。
数列一覧や身近な例(黄金比など)、一般項なども紹介していきますので、ぜひこの記事を通してマスターしてくださいね。
目次
フィボナッチ数列とは?
フィボナッチ数列とは、次のような数列です。
\(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \cdots\)
前の \(2\) 項を足すと次の項が得られるという規則があります。

フィボナッチ数列の定義(漸化式)
つまり、フィボナッチ数列は次の漸化式で定義できます。
\(F_1 = 1\), \(F_2 = 1\)
\(F_{n+2} = F_{n+1} + F_n\)
また、この数列に登場する数は「フィボナッチ数」と呼ばれます。
\(F_0 = 0\) から定義することもあります。
フィボナッチ数列は、「Fibonacci」の頭文字をとって一般項を「\(F_n\)」と表すことが多いです。
フィボナッチとうさぎの問題
フィボナッチ数列は、イタリアの数学者レオナルド・フィボナッチにちなんで名付けられた数列です。
レオナルド・フィボナッチは、うさぎについての次のような問題を出題しました。
\(1\) つがい(オスメスのペア)のうさぎは、産まれて \(2\) か月後から毎月 \(1\) つがいずつのうさぎを産む。
どのうさぎも途中で死なない場合、\(1\) 年の間に全部で何つがいのうさぎになるか。
この問題を解くと、実はどの月におけるつがいの数もフィボナッチ数になっていることがわかります。
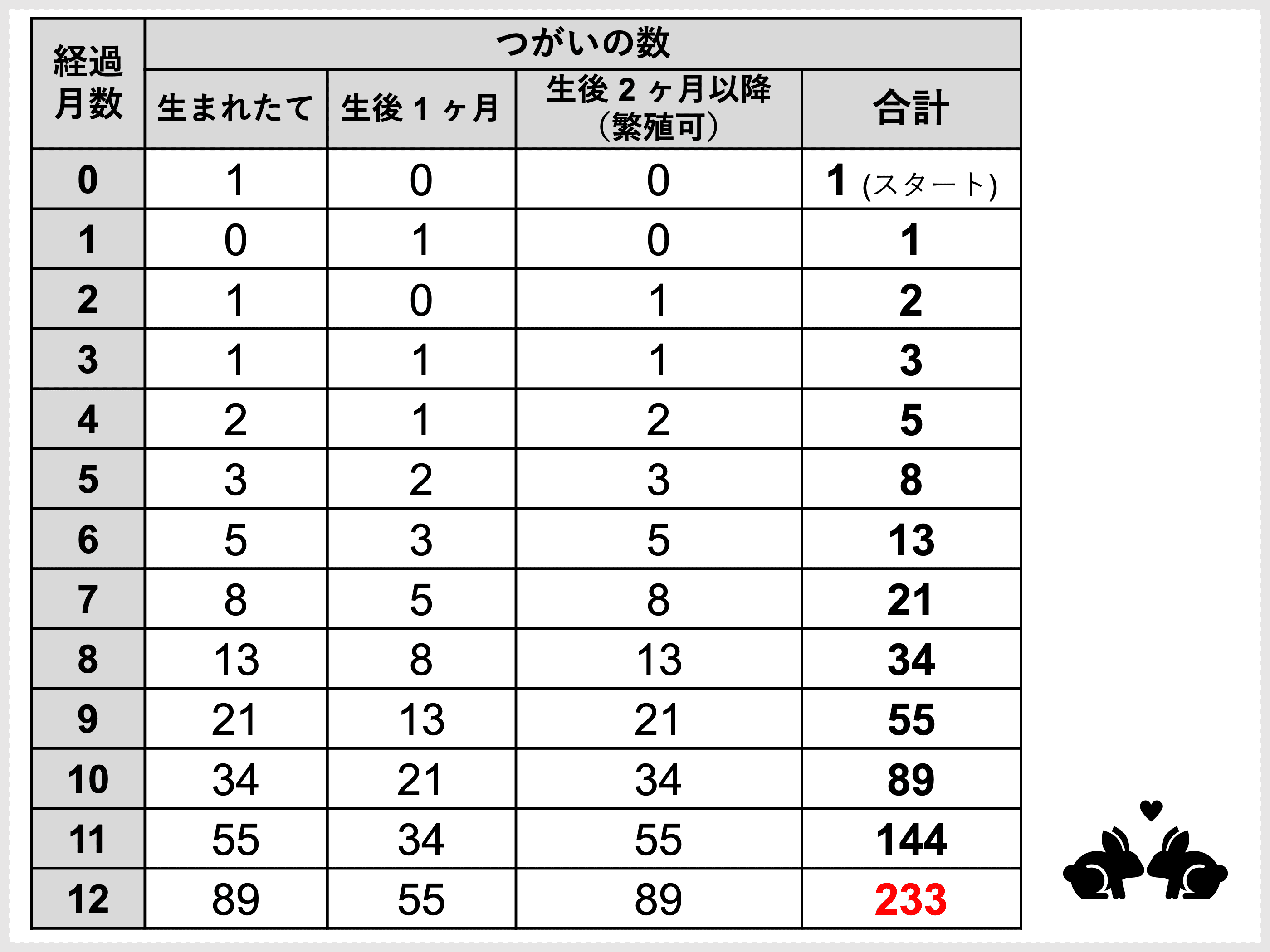
ちなみに答えは \(233\) つがいですね。
フィボナッチ数列は多くの興味深い性質をもち、また自然界のさまざまなところで見られるという不思議な必然性をもっています。
フィボナッチ数の性質
ここでは、フィボナッチ数のさまざまな性質のうち、特によく知られているものを紹介していきます。
フィボナッチ数と長方形・黄金比
フィボナッチ数列の各項を \(1\) 辺の長さとする正方形を並べていきます。
すると、それらの正方形の面積の合計と、並べてできた長方形の面積が一致することから、次の式が成り立ちます。
\begin{align}\displaystyle \sum_{k=1}^n F_k^2 = F_n F_{n + 1}\end{align}
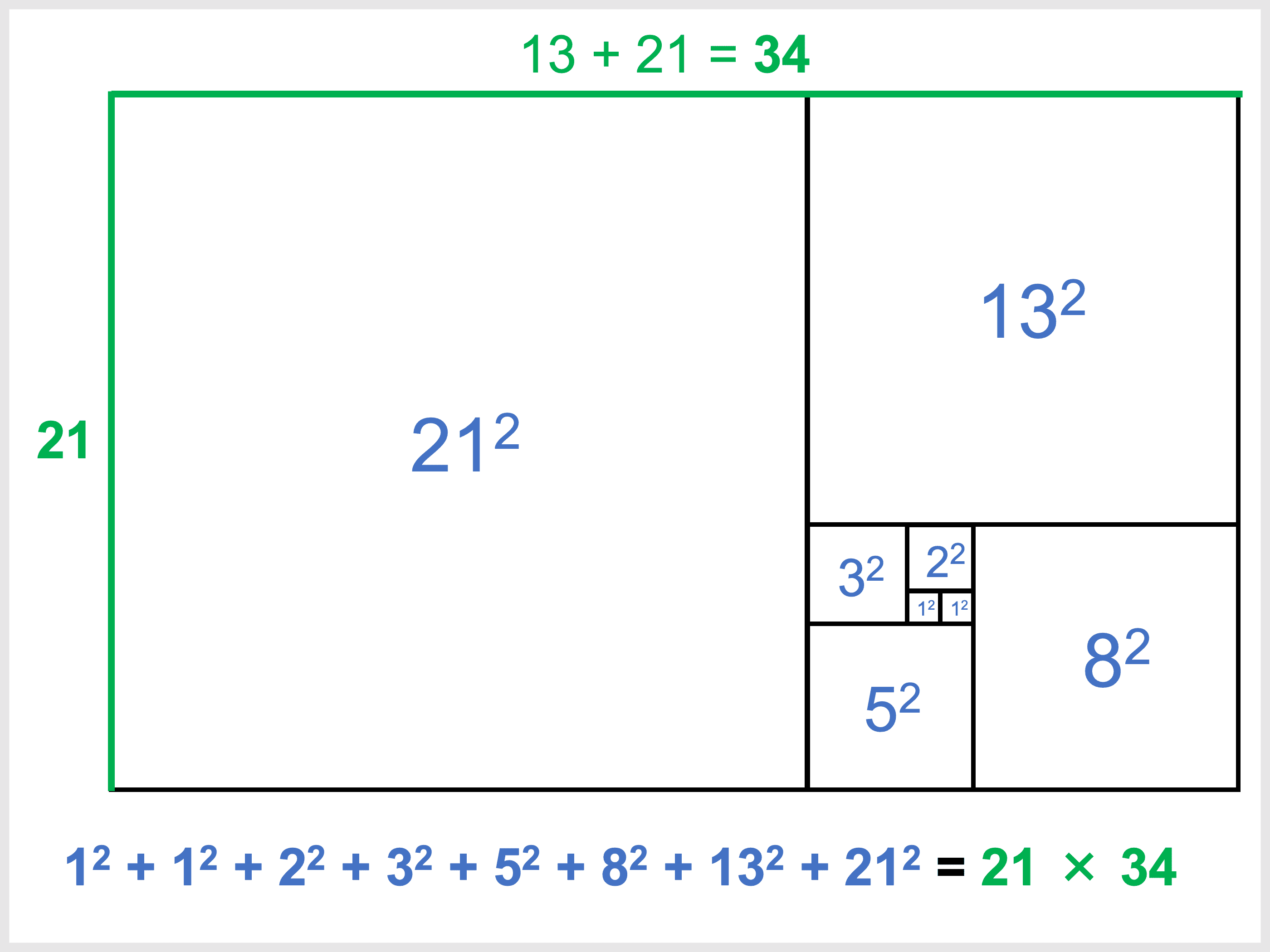
図形で見ると一目瞭然ですね。
また、この長方形の辺の比(隣り合う \(\bf{2}\) 項の比)には面白い性質が隠れています。
隣り合う \(2\) 項の比は黄金比に収束していく。
\begin{align} \lim_{n\to\infty} \frac{F_{n+1}}{F_n} = \frac{1 + \sqrt{5}}{2} = 1.618\cdots \end{align}

この \(\color{red}{1 : 1.618\cdots}\) という比は「黄金比」と呼ばれ、人間がもっとも美しいと感じる比率として有名です。
先ほどの長方形の縦横比が隣り合う \(2\) 項の比に対応していて、正方形を増やすほど黄金比に近づいていきます。

フィボナッチ数と整数の性質
フィボナッチ数には、興味深い整数の性質があります。
例えば、次のような性質があります。
- どの隣り合う \(2\) 項も互いに素である
- フィボナッチ数列の各項を \(5\) 以外の素数で割ってできる余りの列は、周期数列である
- フィボナッチ数列の中から \(2\) つの数を取り出したとき、その \(2\) 数の最大公約数もフィボナッチ数列の中にある
これらの性質は、項数がどれだけ大きくなっても成り立ちます。
実際にフィボナッチ数列の適当な項を選んで試してみてくださいね!
フィボナッチ数の等式
フィボナッチ数において成り立つ等式がたくさん発見されています。
例えば、次の等式が有名です。
\begin{align}F_{n+m} = F_m F_{n+1} + F_{m−1} F_n\end{align}
ほかにもさまざまあるので、ぜひ調べてみてくださいね。
フィボナッチ数列一覧(100番目まで)
ここでは、フィボナッチ数列を第 \(100\) 項まで示します。
先ほど示した性質が本当に成り立つことを、具体的な項でぜひ試してみてください!

フィボナッチ数列の一般項
フィボナッチ数列の一般項は次のような形をしています。
\begin{align}\color{red}{\displaystyle F_n = \frac{1}{\sqrt{5}} \left\{ \left( \frac{1 + \sqrt{5}}{2} \right)^n − \left( \frac{1 − \sqrt{5}}{2} \right)^n \right\}}\end{align}
(見切れる場合は横へスクロール)
一般項の中にも、黄金比 \(\bf{\displaystyle \frac{1 + \sqrt{5}}{2}}\) が現れていますね。
また、無理数 \(\sqrt{5}\) を含む式であるにもかかわらず、\(n\) にどんな自然数を入れても自然数の \(F_n\) が得られることも実に不思議です。
一般項の求め方
上記の一般項は、フィボナッチ数列の定義で示した隣接三項間漸化式を解けば求められます。
「隣接三項間漸化式」の解き方については、以下の記事で説明しています。
 漸化式全パターンの解き方まとめ!難しい問題を攻略しよう
漸化式全パターンの解き方まとめ!難しい問題を攻略しよう
\(F_1 = 1\), \(F_2 = 1\),
\(F_{n+2} = F_{n+1} + F_n\) …① とおく。
特性方程式 \(x^2 − x − 1 = 0\) を解くと、
解の公式より \(\displaystyle x = \frac{1 \pm \sqrt{5}}{2}\)
ここで、
\(\displaystyle \alpha = \frac{1 + \sqrt{5}}{2}\), \(\displaystyle \beta = \frac{1 − \sqrt{5}}{2}\)
とおくと
\(\left\{\begin{array}{l} F_{n+2} − \alpha F_{n+1} = \beta (F_{n+1} − \alpha F_n) \text{…②}\\ F_{n+2} − \beta F_{n+1} = \alpha (F_{n+1} − \beta F_n) \text{…③}\end{array}\right.\)
と変形できる。
また、
\(\begin{align} F_2 − \alpha F_1 &= 1 − \alpha \\ &= 1 − \frac{1 + \sqrt{5}}{2} \\ &= \frac{1 − \sqrt{5}}{2} \\ &= \beta \end{align}\)
\(\begin{align} F_2 − \beta F_1 &= 1 − \beta \\ &= 1 − \frac{1 − \sqrt{5}}{2} \\ &= \frac{1 + \sqrt{5}}{2} \\ &= \alpha \end{align}\)
よって、
②から、数列 \(\{F_{n+1} − \alpha F_n\}\) は初項 \(\beta\)、公比 \(\beta\) の等比数列、
③から、数列 \(\{F_{n+1} − \beta F_n\}\) は初項 \(\alpha\)、公比 \(\alpha\) の等比数列であるから、
\(\left\{\begin{array}{l} F_{n+1} − \alpha F_n = \beta^n \text{…④}\\ F_{n+1} − \beta F_n = \alpha^n \text{…⑤}\end{array}\right.\)
④ − ⑤ より
\((\beta − \alpha)F_n = \beta^n − \alpha^n\)
\(\displaystyle F_n = \frac{\beta^n − \alpha^n}{\beta − \alpha}\)
\(\begin{align} \beta − \alpha &= \frac{1 − \sqrt{5}}{2} − \frac{1 + \sqrt{5}}{2} \\ &= −\sqrt{5} \end{align}\)
であるから、
\(\begin{align} F_n &= \frac{\beta^n − \alpha^n}{−\sqrt{5}} \\ &= \frac{1}{\sqrt{5}} (\alpha^n − \beta^n) \\ &\color{red}{= \frac{1}{\sqrt{5}} \left\{ \left( \frac{1 + \sqrt{5}}{2} \right)^n − \left( \frac{1 − \sqrt{5}}{2} \right)^n \right\}} \end{align}\)
(見切れる場合は横へスクロール)
(証明終わり)
自然界におけるフィボナッチ数列
最後に、自然界で見られるフィボナッチ数や黄金比の例を紹介していきます。
- 花びらの枚数
多くの種類の花において、花びらの枚数がフィボナッチ数になることが知られています。 - 花・実などの螺旋の数
ヒマワリなどの花中央に見られる螺旋の数や、パイナップルや松ぼっくりの表面構造の螺旋の数も、フィボナッチ数であることが知られています。 - 葉のつき方(葉序)
植物の葉同士も、茎を中心に螺旋状に位置をずらして分布します。
太陽の光をすべての葉が得られるようになっているのですね。 - 螺旋構造の比率
螺旋の構造そのものにも、フィボナッチ数列が関係しています。
辺の長さがフィボナッチ数である正方形を並べた長方形において、中央から次の正方形の対角を通るように滑らかな線を繋いでいくと、螺旋構造ができあがります。![]()
このような螺旋構造は、カタツムリ・貝などの殻、ゼンマイのうずまき、台風など、自然界においてよく見られます。 - 人の美的感覚(建造物・美術)
古くから黄金比は人間がもっとも美しいと感じる比率と捉えられ、多くの建造物や美術作品に登場しています。
建造物ではピラミッド・パルテノン神殿など、美術作品ではミロのヴィーナス・モナリザなどが有名ですね。
以上で解説は終わりです。
この記事を通してフィボナッチ数列のおもしろさを感じてもらえたら何よりです!
ほかの数列や漸化式について調べたい方は、以下のまとめ記事から探してみてくださいね!
 数列を総まとめ!一般項・和・漸化式などの重要記事一覧
数列を総まとめ!一般項・和・漸化式などの重要記事一覧

