この記事では、方べき(ほうべき)の定理についてわかりやすく解説していきます。
方べきの定理やその逆の証明、応用問題についても詳しく説明していくので、ぜひこの記事を通してマスターしてくださいね!
目次
方べきの定理とは?
方べきの定理とは、ある円と \(2\) 本の直線が作る図形で、線分の長さの比について成り立つ定理です。
円と直線の位置関係によって、次の \(3\) パターンがあります。
円に引いた \(2\) 本の直線の交点を点 \(\mathrm{P}\)、一方の直線と円の交点を \(\mathrm{A_1}\), \(\mathrm{A_2}\)、もう一方の直線と円の交点を \(\mathrm{B_1}\), \(\mathrm{B_2}\) とおくと、以下が成り立つ。
① \(\bf{2}\) 直線が円の中で交わる場合
\begin{align}\color{red}{\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}}\end{align}

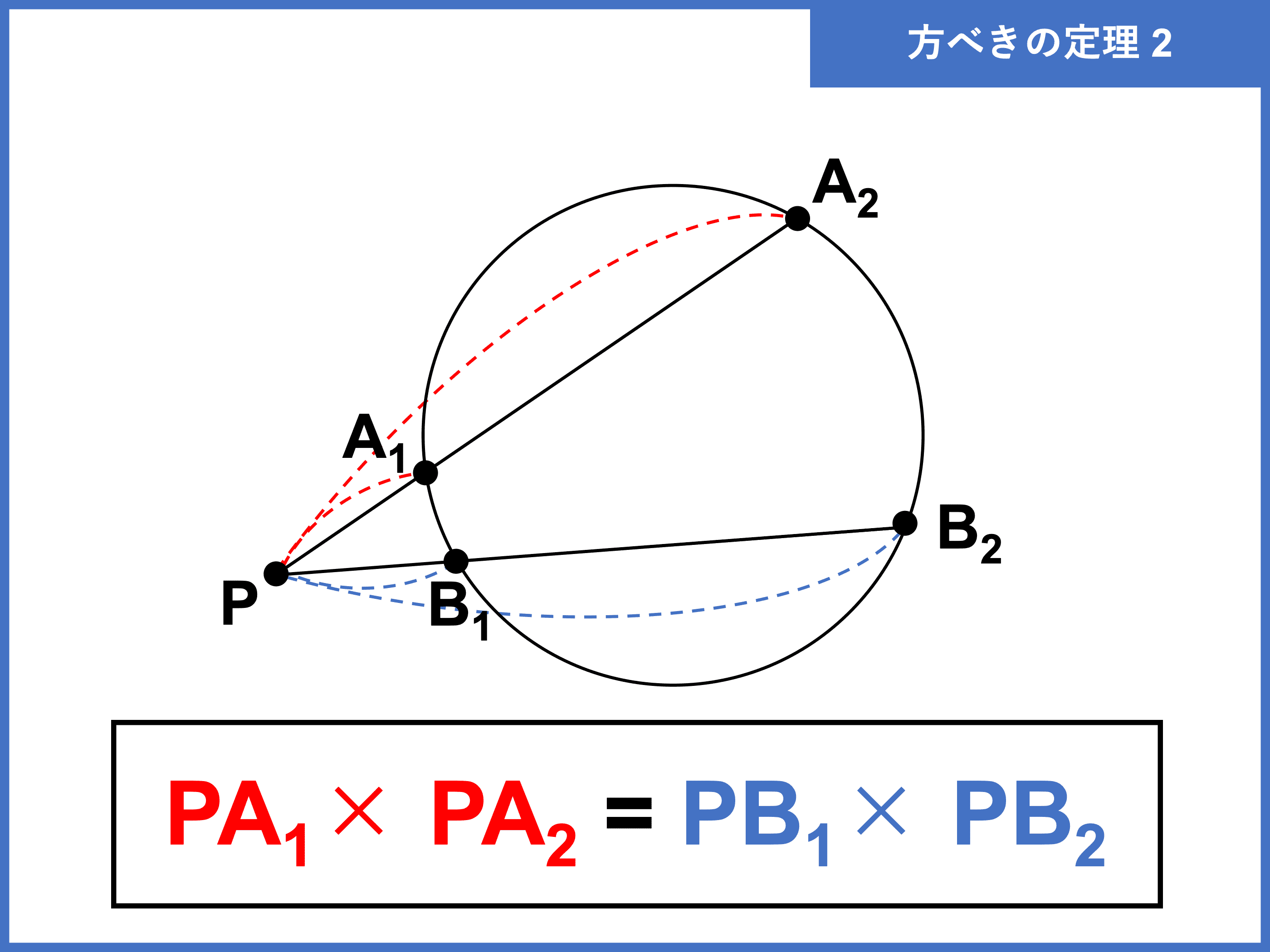
② \(\bf{2}\) 直線が円の外で交わり、円と \(\bf{2}\) 点で交わる場合
\begin{align}\color{red}{\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}}\end{align}
③ 2 直線が円の外で交わり、一方の直線が円の接線である場合
円と接する直線の接点を \(\mathrm{B}\) とおくと、
\begin{align}\color{red}{\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB^2}}\end{align}

パターンごとに見た目は違いますが、方べきの定理が成り立つ線分の関係はまったく同じなのに気づいたでしょうか?
各直線において、点 \(\mathrm{P}\) から直線と円の交点までの長さの積 \(\mathrm{PA_1} \cdot \mathrm{PA_2}\) と \(\mathrm{PB_1} \cdot \mathrm{PB_2}\) が等しいという関係です。
(パターン \(3\) では、\(\mathrm{B_1}\) と \(\mathrm{B_2}\) が一致したと考える)
ですので、\(3\) パターン別々に覚えるのではなく、「円に \(\bf{2}\) 本の直線が引かれたら成り立つ性質」=「方べきの定理」ととらえるようにしましょう!
方べきの定理の証明
方べきの定理①〜③の証明について説明します。
どのパターンでも、補助線を引いてできる \(2\) つの三角形の相似を示すことで方べきの定理を証明できます。
方べきの定理①の証明
図のように円の中で交わる \(2\) 直線において、以下が成り立つことを証明せよ。
\begin{align}\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}\end{align}

\(\mathrm{A_1}\) と \(\mathrm{B_1}\)、\(\mathrm{A_2}\) と \(\mathrm{B_2}\) を結ぶ補助線を引くと、\(\triangle \mathrm{PA_1B_1}\) と \(\triangle \mathrm{PB_2A_2}\) が相似となることに注目します。
\(\triangle \mathrm{PA_1B_1}\) と \(\triangle \mathrm{PB_2A_2}\) において、
対頂角は等しいので、
\(\angle \mathrm{A_1PB_1} = \angle \mathrm{B_2PA_2}\) …①
同じ弧に対する円周角は等しいので、
\(\angle \mathrm{B_1A_1P} = \angle \mathrm{A_2B_2P}\) …②
(円周角の定理)

①、②より、\(2\) 組の角がそれぞれ等しいので、
\(\triangle \mathrm{PA_1B_1}\) ∽ \(\triangle \mathrm{PB_2A_2}\)
相似な三角形において、対応する辺の比は等しいので、
\(\mathrm{PA_1} : \mathrm{PB_2} = \mathrm{PB_1} : \mathrm{PA_2}\)
よって、
\(\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}\)
が成り立つ。
(証明終わり)
方べきの定理②の証明
図のように円の外で交わる \(2\) 直線において、以下が成り立つことを証明せよ。
\begin{align}\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}\end{align}

\(\mathrm{A_1}\) と \(\mathrm{B_1}\)、\(\mathrm{A_2}\) と \(\mathrm{B_2}\) を結ぶ補助線を引くと、先ほどと同様、\(\triangle \mathrm{PA_1B_1}\) と \(\triangle \mathrm{PB_2A_2}\) が相似となります。
\(\triangle \mathrm{PA_1B_1}\) と \(\triangle \mathrm{PB_2A_2}\) において、
円に内接する四角形の内角は、その向かい合う角の外角と等しいので、
\(\angle \mathrm{PB_1A_1} = \angle \mathrm{PA_2B_2}\) …①
共通な角より、
\(\angle \mathrm{A_1PB_1} = \angle \mathrm{B_2PA_2}\) …②

①、②より、\(2\) 組の角がそれぞれ等しいので、
\(\triangle \mathrm{PA_1B_1}\) ∽ \(\triangle \mathrm{PB_2A_2}\)
相似な三角形において、対応する辺の比は等しいので、
\(\mathrm{PA_1} : \mathrm{PB_2} = \mathrm{PB_1} : \mathrm{PA_2}\)
よって、
\(\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB_1} \times \mathrm{PB_2}\)
が成り立つ。
(証明終わり)
方べきの定理③の証明
図のように円と \(2\) 点で交わる直線と円の接線が、円の外側で交点をもつとき、以下が成り立つことを証明せよ。
\begin{align}\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB^2}\end{align}

\(\mathrm{A_1}\) と \(\mathrm{B}\)、\(\mathrm{A_2}\) と \(\mathrm{B}\) を結ぶ補助線を引きます。
一方の直線が円の接線なので、接弦定理を用いると \(\triangle \mathrm{PA_1B}\) と \(\triangle \mathrm{PBA_2}\) が相似であることを示せます。
\(\triangle \mathrm{PA_1B}\) と \(\triangle \mathrm{PBA_2}\) において、
接弦定理より、
\(\angle \mathrm{PBA_1} = \angle \mathrm{PA_2B}\) …①
また共通な角より、
\(\angle \mathrm{A_1PB} = \angle \mathrm{BPA_2}\) …②

①、②より、\(2\) 組の角がそれぞれ等しいので、
\(\triangle \mathrm{PA_1B}\) ∽ \(\triangle \mathrm{PBA_2}\)
相似な三角形において、対応する辺の比は等しいので、
\(\mathrm{PA_1} : \mathrm{PB} = \mathrm{PB} : \mathrm{PA_2}\)
よって、
\(\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB} \times \mathrm{PB}\)
つまり
\(\mathrm{PA_1} \times \mathrm{PA_2} = \mathrm{PB^2}\)
が成り立つ。
(証明終わり)
どれも、\(2\) 直線と円が作る三角形の相似関係から導けました。
証明の中で「円周角の定理」や「接弦定理」を使ったように、円が関わるからこそ成り立つ定理なのですね。
方べきの定理の逆とは?
方べきの定理は、その逆も成り立ちます。
頂点の記号の表記を変えますが、関係性を理解してみてくださいね。
① \(2\) 本の線分 \(\mathrm{AB}\), \(\mathrm{CD}\) が点 \(\mathrm{P}\) で交わる場合
「\(\color{red}{\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}}\)」が成り立つならば、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にある。
② \(2\) 本の線分 \(\mathrm{AB}\), \(\mathrm{CD}\) の延長が点 \(\mathrm{P}\) で交わる場合
「\(\color{red}{\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}}\)」が成り立つならば、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にある。
③ 線分 \(\mathrm{AB}\) の延長上に点 \(\mathrm{P}\) がある場合
直線 \(\mathrm{AB}\) 上にない点 \(\mathrm{T}\) に対し、「\(\color{red}{\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}}\)」が成り立つならば、\(\mathrm{PT}\) は \(\mathrm{\triangle TAB}\) の外接円に接する。
\(4\) つの線分(または \(3\) つの線分)の積に関する等式が成り立てば、円の存在を証明できるということですね。
方べきの定理の逆の証明
方べきの定理の逆についても、①〜③をそれぞれ証明していきます。
方べきの定理①の逆の証明
\(2\) 本の線分 \(\mathrm{AB}\), \(\mathrm{CD}\) が点 \(\mathrm{P}\) で交わるとき、\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\) が成り立つならば、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にあることを証明せよ。
線分の積に関する等式から、線分の長さの比が得られます。
それを利用して三角形の相似を示し、角度の情報から円の存在を示しましょう。
\(\triangle \mathrm{PAC}\) と \(\triangle \mathrm{PDB}\) において、
仮定より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
つまり、
\(\mathrm{PA} : \mathrm{PD} = \mathrm{PC} : \mathrm{PB}\) …①
対頂角は等しいので
\(\angle \mathrm{APC} = \angle \mathrm{DPB}\) …②

①、②より、\(2\) 組の辺の比とその間の角がそれぞれ等しいので
\(\triangle \mathrm{PAC}\) ∽ \(\triangle \mathrm{PDB}\)
相似な三角形では、対応する角の大きさはそれぞれ等しいので
\(\angle \mathrm{PAC} = \angle \mathrm{PDB}\)

よって、円周角の定理の逆より、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にある。
(証明終わり)
方べきの定理②の逆の証明
\(2\) 本の線分 \(\mathrm{AB}\), \(\mathrm{CD}\) の延長が点 \(\mathrm{P}\) で交わるとき、\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\) が成り立つならば、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にあることを証明せよ。
こちらも、先ほどと同様の流れで証明していきます。
\(\triangle \mathrm{PAC}\) と \(\triangle \mathrm{PDB}\) において、
仮定より
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
つまり、
\(\mathrm{PA} : \mathrm{PD} = \mathrm{PC} : \mathrm{PB}\) …①
共通な角より、
\(\angle \mathrm{APC} = \angle \mathrm{DPB}\) …②

①、②より、\(2\) 組の辺の比とその間の角がそれぞれ等しいので、
\(\triangle \mathrm{PAC}\) ∽ \(\triangle \mathrm{PDB}\)
相似な三角形において、対応する角の大きさはそれぞれ等しいので、
\(\angle \mathrm{PAC} = \angle \mathrm{PDB}\)
ここで、\(\angle \mathrm{BAC}\) は \(\angle \mathrm{PAC}\) の外角であるから、
\(\begin{align} \angle \mathrm{BAC} &= 180^\circ − \angle \mathrm{PAC} \\ &= 180^\circ − \angle \mathrm{PDB} \end{align}\)

よって、四角形 \(\mathrm{ABCD}\) の対角の和が \(180^\circ\) であることから、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にある。
(証明終わり)
方べきの定理③の逆の証明
線分 \(\mathrm{AB}\) の延長上に点 \(\mathrm{P}\) があり、直線 \(\mathrm{AB}\) 上にない点 \(\mathrm{T}\) に対し、\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}\) が成り立つならば、\(\mathrm{PT}\) は \(\triangle \mathrm{TAB}\) の外接円に接することを証明せよ。
円に接することの証明なので、接弦定理をイメージしましょう。
\(\triangle \mathrm{PTA}\) と \(\triangle \mathrm{PBT}\) において、
仮定より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}\)
つまり、
\(\mathrm{PA} : \mathrm{PT} = \mathrm{PT} : \mathrm{PB}\) …①
共通な角より、
\(\angle \mathrm{TPA} = \angle \mathrm{BPT}\) …②

①、②より、\(2\) 組の辺の比とその間の角がそれぞれ等しいので、
\(\triangle \mathrm{PTA}\) ∽ \(\triangle \mathrm{PBT}\)
相似な三角形において、対応する角の大きさはそれぞれは等しいので、
\(\angle \mathrm{PTA} = \angle \mathrm{PBT}\)

よって、接弦定理の逆より、\(\mathrm{PT}\) は \(\triangle \mathrm{TAB}\) の外接円に接する。
(証明終わり)
方べきの定理の使い方
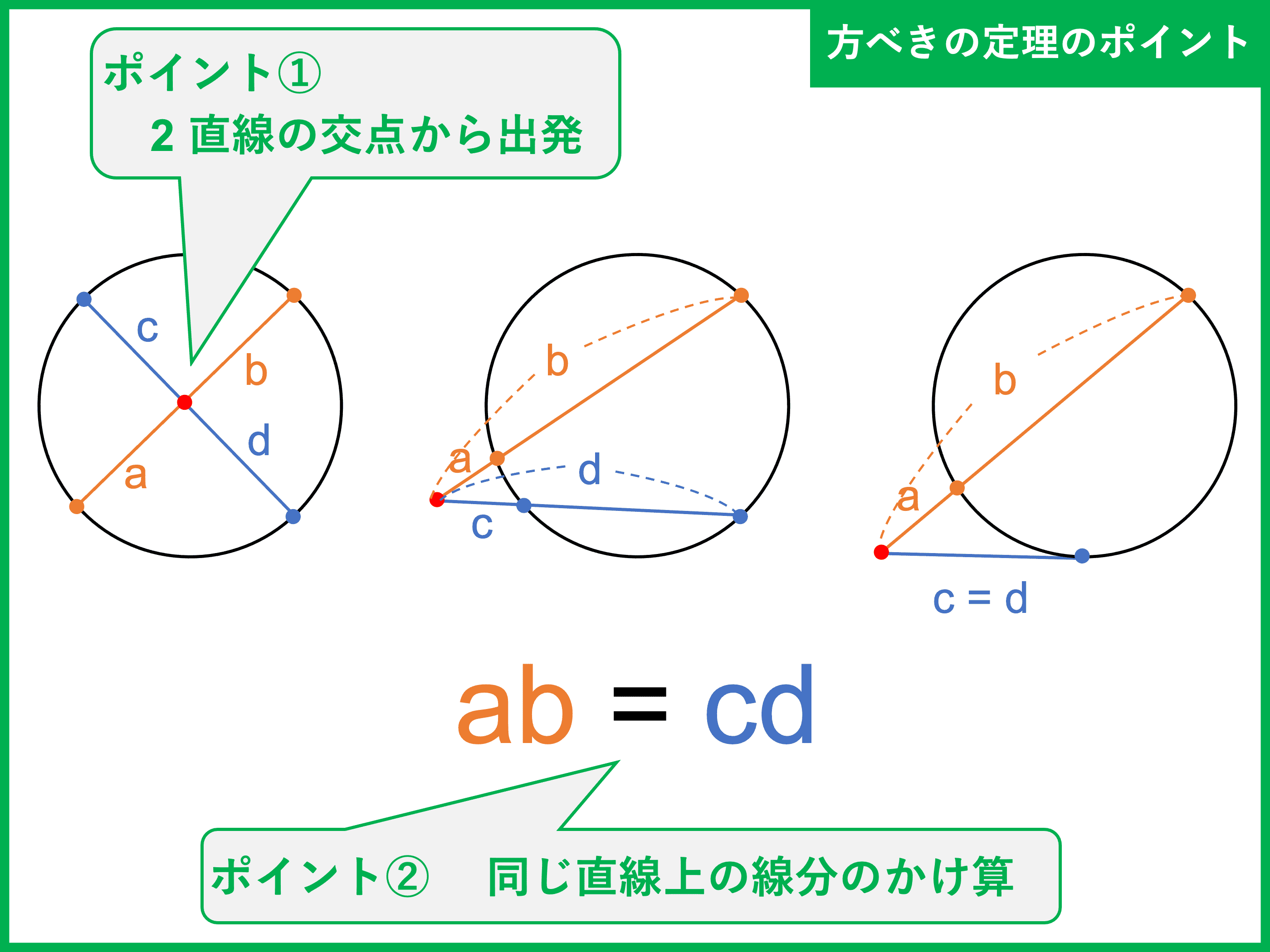
\(2\) 直線と円が出てきたら、「方べきの定理が使えるかも?」とアンテナを張っておきましょう。
方べきの定理を使う際は、① \(2\) 直線の交点から出発すること、② 同じ直線上の点までの線分のかけ算であることの \(2\) 点を押さえておけばバッチリです。
それでは、練習問題を通して方べきの定理の使い方を説明します。
練習問題①「線分の長さを求める」
下の図において、\(x\) の値を求めなさい。


円と \(2\) 本の直線があるので、それぞれ方べきの定理が利用できますね。
計算する値を間違えないようにしましょう。
(1) 方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
\(x \times 2x = 5 \times 11\)
\(2x^2 = 55\)
\(\displaystyle x^2 = \frac{55}{2}\)
\(x > 0\) より、
\(\displaystyle x = \frac{\sqrt{55}}{\sqrt{2}} = \frac{\sqrt{110}}{2}\)
答え: \(\color{red}{\displaystyle \frac{\sqrt{110}}{2}}\)
(2) 方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}\)
\(2 \times 8 = x^2\)
\(x^2 = 16\)
\(x > 0\) より、
\(x = 4\)
答え: \(\color{red}{4}\)
練習問題②「辺の長さを求める」
下の図において、\(x\) の値を求めなさい。


方べきの定理にかかわる長さを \(x\) を使って表してみましょう。
(1) 方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
\((x − 6) \times 6 = 2 \times 3\)
\(6x − 36 = 6\)
\(6x = 42\)
\(x = 7\)
答え: \(\color{red}{7}\)
(2) \(\mathrm{CO}\) は円の半径なので、\(\mathrm{CO} = \mathrm{OD} = 4\)
よって、
\(\mathrm{PC} = x − 4\)
方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
\(3 \times 9 = (x − 4)(x + 4)\)
\(27 = x^2 − 16\)
\(x^2 = 43\)
\(x > 0\) より、
\(x = \sqrt{43}\)
答え: \(\color{red}{\sqrt{43}}\)
(3) 方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}\)
\(4 \times (4 + x) = 8^2\)
\(16 + 4x = 64\)
\(4x = 48\)
\(x = 12\)
答え: \(\color{red}{12}\)
方べきの定理の応用問題
最後に、方べきの定理の応用問題にチャレンジしましょう。
応用問題「4 点が同一円周上にあることを証明する」
点 \(\mathrm{T}\) で接する \(2\) つの円 \(X\)、\(Y\) がある。\(2\) つの円の接点 \(\mathrm{T}\) を通る共通接線上に点 \(\mathrm{P}\) をとる。点 \(\mathrm{P}\) から \(2\) つの円にそれぞれ直線を引き、円 \(X\) との交点を \(\mathrm{A}\) と \(\mathrm{B}\)、円 \(Y\) との交点を \(\mathrm{C}\)、\(\mathrm{D}\) とする。このとき、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) が同一円周上にあることを証明せよ。


「\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) が同一円周上にあること」の証明なので、方べきの定理の逆を利用できそうですね。
まずは円 \(X\), \(Y\) のそれぞれに方べきの定理を適用し、得られた線分の積に関する等式を利用しましょう。
円 \(X\) において、方べきの定理より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PT^2}\) …①
また、円 \(Y\) においても方べきの定理より、
\(\mathrm{PC} \times \mathrm{PD} = \mathrm{PT^2}\) …②
①、②より、
\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\)
よって、\(2\) 本の直線の延長が点 \(\mathrm{P}\) で交わり、\(\mathrm{PA} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{PD}\) が成り立つので、
方べきの定理の逆より、\(4\) 点 \(\mathrm{A}\)、\(\mathrm{B}\)、\(\mathrm{C}\)、\(\mathrm{D}\) は同一円周上にある。
(証明終わり)
以上で応用問題も終わりです!
方べきの定理について理解が深まりましたか?
図形問題や証明で使うことの多い定理なので、しっかりとマスターしておきましょう!



