この記事では、「点と直線の距離」の公式や証明をわかりやすく解説していきます。
\(3\) 次元(座標空間)の公式や計算問題の解き方も説明していますので、ぜひこの記事を通してマスターしてくださいね!
目次
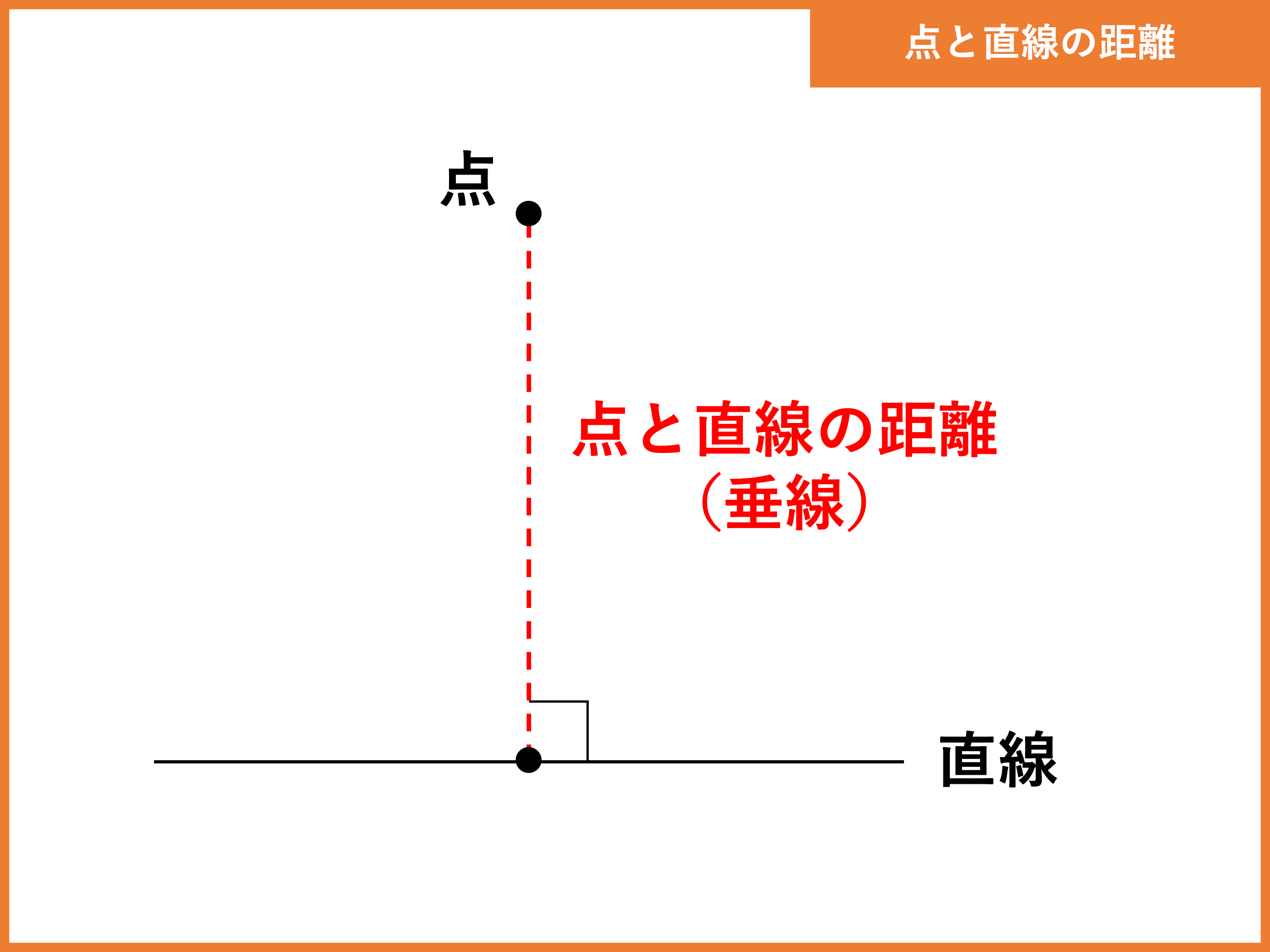
点と直線の距離とは?
点と直線の距離とは、点から直線に向けて引いた垂線の長さであり、最短距離のことです。
点と直線の距離の公式
点と直線の距離の公式は次の通りです。
点 \(\mathrm{A}(x_1, y_1)\) と直線 \(\ell\) : \(ax + by + c = 0\) の距離 \(D\) は
\begin{align}\color{red}{\displaystyle D = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}}\end{align}
特に、原点 \(\mathrm{O}(0, 0)\) と直線 \(\ell\) との距離 \(D\) は
\begin{align}\color{red}{\displaystyle D = \frac{|c|}{\sqrt{a^2 + b^2}}}\end{align}
このとき、直線の方程式を一般形で表すのがポイントです。
直線の方程式の形
- 一般形: \(ax + by + c = 0\)
- 基本形: \(y = ax + b\)
- 切片形: \(\displaystyle \frac{x}{a} + \frac{y}{b} = 1\)
点と直線の距離の公式の使い方
公式の使い方を以下の例題で説明します。
(1) 原点と直線 \(x + 3y + 4 = 0\) の距離を求めよ。
(2) 直線 \(y = −x + 4\) と点 \((4, 6)\) の距離を求めよ。
(1) では、点の座標が原点 \((0, 0)\) となります。
(2) では、直線の方程式を一般形に直してから公式に当てはめましょう。
(1)
原点 \((0, 0)\)と直線 \(x + 3y + 4 = 0\) の距離を \(D\) とおくと、
\(\begin{align} D &= \frac{|1 \cdot 0 + 3 \cdot 0 + 4|}{\sqrt{1^2 + 3^2}} \\ &= \frac{|0 + 0 + 4|}{\sqrt{1 + 9}}\\ &= \frac{4}{\sqrt{10}} \\ &= \frac{4\sqrt{10}}{10} \\ &= \frac{2\sqrt{10}}{5}\end{align}\)
答え: \(\displaystyle \frac{2\sqrt{10}}{5}\)
(2)
\(y = −x + 4\) を変形して
\(x + y − 4 = 0\)
点\((4, 6)\) と直線 \(x + y − 4 = 0\) の距離を \(D\) とおくと、
\(\begin{align} D &= \frac{|1 \cdot 4 + 1 \cdot 6 − 4|}{\sqrt{1^2 + 1^2}} \\ &= \frac{|−4 − 6 + 4|}{\sqrt{2}} \\ &= \frac{6}{\sqrt{2}} \\ &= \frac{6\sqrt{2}}{2} \\ &= 3\sqrt{2} \end{align}\)
答え: \(3\sqrt{2}\)
点と直線の距離の証明
ここでは、点と直線の距離の公式を \(2\) 通りの方法(三角形の面積の利用、ベクトルの利用)で証明します。
点 \(\mathrm{A}(x_1, y_1)\) と直線 \(\ell\) : \(ax + by + c = 0\) の距離 \(D\) が
\begin{align}\displaystyle D = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}\end{align}
となることを証明せよ。
証明① 三角形の面積の利用
まずは、三角形の面積を利用した証明です。
直角の頂点 \(\mathrm{A}\) をもち、直線 \(\ell\) 上に斜辺をとる直角三角形を考え、この三角形の面積を \(2\) 通りの方法で表すのがポイントです。
点 \(\mathrm{A}\) から直線 \(\ell\) に下ろした垂線の足を \(\mathrm{H}\) とおく。
また、点 \(\mathrm{A}\) と \(x\) 座標が同じな \(\ell\) 上の点を \(\mathrm{P}(x_1, y_\mathrm{P})\)、点 \(\mathrm{B}\) と \(y\) 座標が同じな \(\ell\) 上の点を \(\mathrm{Q}(x_\mathrm{Q}, y_1)\) とする。
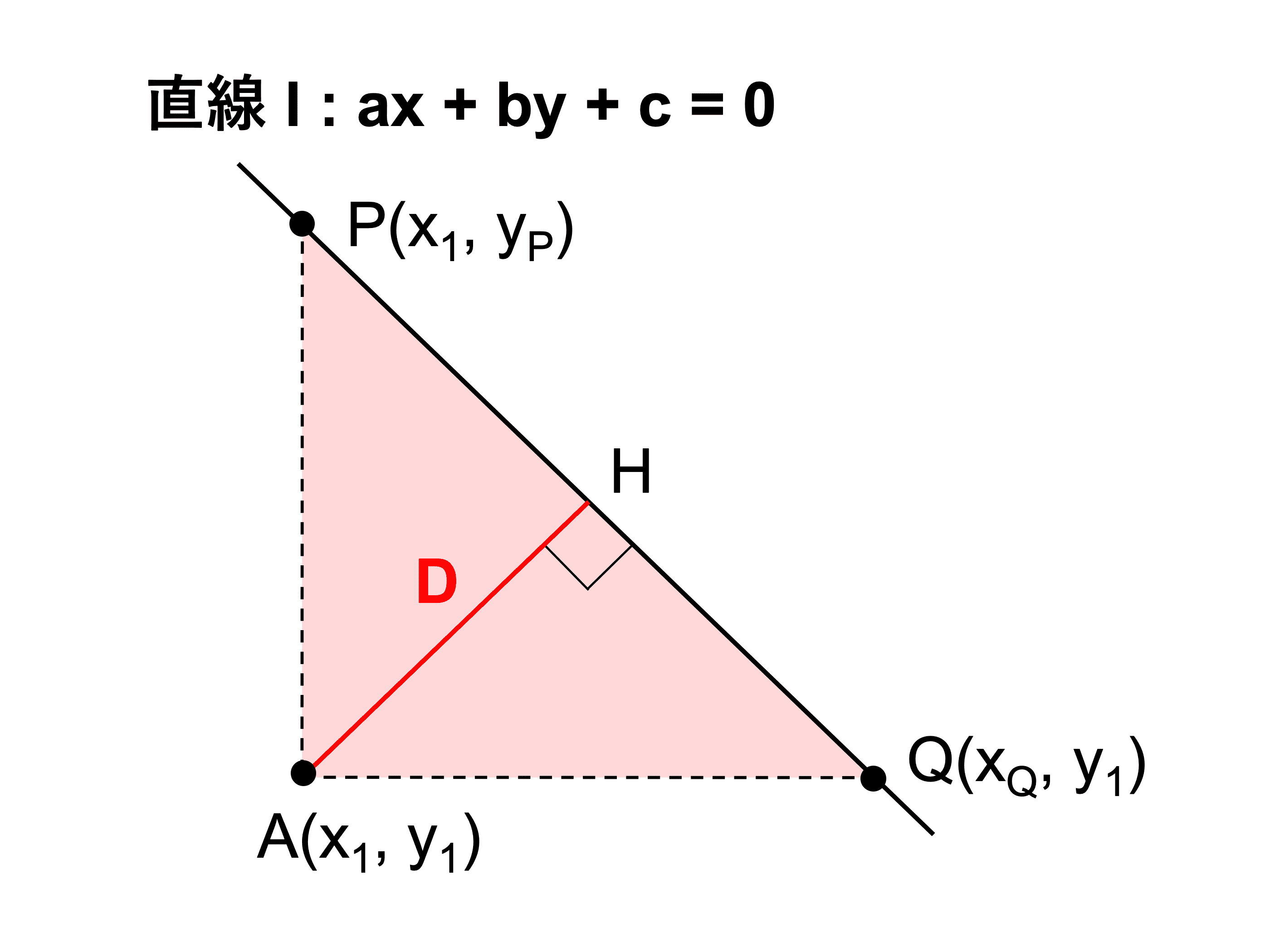
\(\triangle \mathrm{PAQ}\) の面積 \(S\) は次の \(2\) 通りの方法で表すことができる。
- \(\displaystyle S = \frac{1}{2} \mathrm{AP} \cdot \mathrm{AQ}\) …①
- \(\displaystyle S = \frac{1}{2} \mathrm{PQ} \cdot \mathrm{AH}\) …②
\(\mathrm{AP} = p\), \(\mathrm{AQ} = q\) とおくと、
\(\begin{align} \mathrm{PQ} &= \sqrt{\mathrm{AP}^2 + \mathrm{AQ}^2} \\ &= \sqrt{p^2 + q^2} \end{align}\)
①より
\(\displaystyle S = \frac{1}{2} pq\)
②より
\(\displaystyle S = \frac{1}{2} D \sqrt{p^2 + q^2}\)
よって
\(\displaystyle \frac{1}{2} pq = \frac{1}{2} D \sqrt{p^2 + q^2}\)
\(\displaystyle D = \frac{pq}{\sqrt{p^2 + q^2}}\) …③
ここで、
\(p = \mathrm{AP} = |y_\mathrm{P} − y_1|\)
\(\mathrm{P}(x_1, y_\mathrm{P})\) は直線 \(\ell\) 上の点であるから、
\(ax_1 + by_\mathrm{P} + c = 0\)
\(\displaystyle y_\mathrm{P} = −\frac{ax_1 + c}{b}\)
よって
\(\begin{align} p &= \left| −\frac{ax_1 + c}{b} − y_1 \right| \\ &= \frac{1}{|b|} |−ax_1 − c − by_1| \\ &= \frac{1}{|b|} |ax_1 + by_1 + c| \text{ …④}\end{align}\)
\(q = \mathrm{AQ} = |x_\mathrm{Q} − x_1|\)
\(\mathrm{Q}(x_\mathrm{Q}, y_1)\) は直線 \(\ell\) 上の点であるから、
\(ax_\mathrm{Q} + by_1 + c = 0\)
\(\displaystyle x_\mathrm{Q} = −\frac{by_1 + c}{a}\)
よって
\(\begin{align} q &= \left| −\frac{by_1 + c}{a} − x_1 \right| \\ &= \frac{1}{|a|} |−by_1 − c − ax_1| \\ &= \frac{1}{|a|} |ax_1 + by_1 + c| \text{ …⑤}\end{align}\)
④、⑤を③に代入すると、
\(\begin{align}D &= \frac{\frac{1}{|b|} |ax_1 + by_1 + c| \cdot \frac{1}{|a|} |ax_1 + by_1 + c|}{\sqrt{\frac{1}{b^2} (ax_1 + by_1 + c)^2 + \frac{1}{a^2} (ax_1 + by_1 + c)^2}}\\&= \displaystyle \frac{\frac{1}{|ab|}(ax_1 + by_1 + c)^2}{\sqrt{(ax_1 + by_1 + c)^2 \frac{a^2 + b^2}{a^2b^2}}}\\&= \displaystyle \frac{\frac{1}{|ab|} (ax_1 + by_1 + c)^2}{|ax_1 + by_1 + c| \frac{\sqrt{a^2 + b^2}}{|ab|}}\\&= \frac{1}{|ab|} (ax_1 + by_1 + c)^2 \cdot \frac{|ab|}{|ax_1 + by_1 + c| \sqrt{a^2 + b^2}}\\&= \displaystyle \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}\end{align}\)
(見切れる場合は横へスクロール)
したがって、
\(\displaystyle D = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}\) は成り立つ。
(証明終わり)
計算は大変でしたが、無事に導けましたね。
証明② ベクトルの利用
続いて、ベクトルを利用した証明です。
直線 \(\ell\) の法線ベクトルが求めたいベクトル(距離 \(D\) をとる線分)と平行であることに着目します。
直線 \(\ell: ax + by + c = 0\) の法線ベクトルを \(\vec{n}\) とおくと、
\(\vec{n} = (a, b)\)

\(\mathrm{H}\) の座標を \((X, Y)\) とすると、
\(\overrightarrow{\mathrm{AH}} = (X − x_1, Y − y_1)\)
\(\overrightarrow{\mathrm{AH}}\) は \(\ell\) の法線ベクトルと平行なので、実数 \(t\) を用いて
\((X − x_1, Y − y_1) = t(a, b)\) …①
と表せる。
点 \(\mathrm{H}\) が \(\ell\) 上にあるには、\(aX + bY + c = 0\) を満たす \(t\) を求めればよい。
①の両辺に対して、\((a, b)\) との内積をとると
\(a(X − x_1) + b(Y − y_1) = ta \cdot a + tb \cdot b\)
\(aX − ax_1 + bY − by_1 = t(a^2 + b^2)\)
これと、\(aX + bY = −c\) より
\(−c − ax_1 − by_1 = t(a^2 + b^2)\)
\(a^2 + b^2 \neq 0\) より、
\(\displaystyle t = −\frac{ax_1 + by_1 + c}{a^2 + b^2}\)
よって、\(\mathrm{AH}\) の長さ、すなわち \(t(a, b)\) の長さは
\(\begin{align} D &= |t| \sqrt{a^2 + b^2} \\ &= \frac{|ax_1 + by_1 + c|}{a^2 + b^2} \cdot \sqrt{a^2 + b^2} \\ &= \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}} \end{align}\)
したがって、与式は成り立つ。
(証明終わり)
計算式だけで理解しようとすると混乱するので、図をよく見ながら理解していきましょう。
【発展】点と平面の距離の公式(3次元)
二次元では「点と直線の距離」ですが、三次元(座標空間)では「点と平面の距離」の公式があります。
点 \(\mathrm{A}(x_1, y_1, z_1)\) と平面 \(\alpha\) : \(ax + by + cz + d = 0\) の距離 \(D\) は
\begin{align}\color{red}{\displaystyle D = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}}}\end{align}
特に、原点 \(\mathrm{O}(0, 0, 0)\) と直線 \(\ell\) との距離 \(D\) は
\begin{align}\color{red}{\displaystyle D = \frac{|d|}{\sqrt{a^2 + b^2 + c ^2}}}\end{align}
ある点からある平面への最短距離のことですね。
点と直線の距離(図の左側)と、点と平面との距離(図の右側)はこのようなイメージです。

二次元のときと同様、平面の方程式を一般形で表すのがポイントです。
平面の方程式の形
- 一般形: \(ax + by + cz + d = 0\)
- 基本形: \(z = ax + by + c\)
- 切片形: \(\displaystyle \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)
点と平面の距離の公式の使い方
点と平面の距離の公式の使い方も、基本的には二次元(点と直線の距離)のときと変わりません。
以下の例題を参考にしてみてくださいね。
平面 \(z = 3x − 2y + 2\) と点 \((4, 5, 0)\) の距離を求めよ。
平面の方程式を一般形に変形して、点と平面の距離の公式に当てはめます。
\(z = 3x − 2y + 2\) を変形して
\(3x − 2y − z + 2 = 0\)
点 \((4, 5, 0)\) と平面 \(3x − 2y − z + 2 = 0\) の距離を \(D\) とおくと、
\(\begin{align}\displaystyle D &= \frac{|3 \cdot 4 + (−2) \cdot 5 + (−1) \cdot 0 + 2|}{\sqrt{3^2 + (−2)^2 + (−1)^2}} \\&= \frac{|12 − 10 + 0 + 2|}{\sqrt{9 + 4 + 1}} \\&= \frac{|4|}{\sqrt{14}} \\&= \frac{4\sqrt{14}}{14} \\&= \frac{2\sqrt{14}}{7}\end{align}\)
答え: \(\displaystyle \frac{2\sqrt{14}}{7}\)
点と直線の距離の計算問題
それでは、点と直線の距離の計算問題に挑戦しましょう。
計算問題①「距離から直線の方程式を求める」
点 \((−1, 2)\) と直線 \(y = a(x + 2) + 5\) の距離が \(1\) のとき、\(a\) の値を求めよ。

直線を一般形に直して、点と直線の距離の式を立てます。
その値が \(1\) であることから、定数 \(a\) を求めましょう。
\(y = a(x + 2) + 5\) を変形して
\(y = ax + 2a + 5\)
\(ax − y + 2a + 5 = 0\)
点 \((−1, 2)\) と直線 \(ax − y + 2a + 5 = 0\) の距離を \(D\) とおくと、
\(\begin{align}D &= \displaystyle \frac{|a \cdot (−1) + (−1) \cdot 2 + 2a + 5|}{\sqrt{a^2 + (−1)^2}} \\&= \frac{|−a − 2 + 2a + 5|}{\sqrt{a^2 + 1}} \\&= \frac{|a + 3|}{\sqrt{a^2 + 1}}\end{align}\)
\(D = 1\) より
\(\displaystyle \frac{|a + 3|}{\sqrt{a^2 + 1}} = 1\)
両辺を \(2\) 乗して
\(\displaystyle \frac{a^2 + 6a + 9}{a^2 + 1} = 1\)
\(a^2 + 6a + 9 = a^2 + 1\)
\(6a = −8\)
\(a = −\displaystyle \frac{8}{6} = −\displaystyle \frac{4}{3}\)
答え: \(\color{red}{a = −\displaystyle \frac{4}{3}}\)
計算問題②「平行な 2 直線の距離を求める」
平行な \(2\) 直線 \(3x − 4y + 5 = 0\)、\(3x − 4y − 1 = 0\) の距離を求めよ。

平行な \(2\) 直線なので、直線上のどこをとっても距離は一定です。
一方の直線上の \(1\) 点と、もう一方の直線の距離を求めましょう。
直線 \(3x − 4y + 5 = 0\) 上の点 \((−3, −1)\) と直線 \(3x − 4y − 1 = 0\) の距離は
\(\displaystyle \frac{|3 \cdot (−3) + (−4) \cdot (−1) − 1|}{\sqrt{3^2 + (−4)^2}}\)
\(= \displaystyle \frac{|−9 + 4 − 1|}{\sqrt{9 + 16}}\)
\(= \displaystyle \frac{|−6|}{\sqrt{25}}\)
\(= \displaystyle \frac{6}{5}\)
答え: \(\color{red}{\displaystyle \frac{6}{5}}\)
計算問題③「頂点の座標から三角形の面積を求める」
\(\mathrm{A}(−1, −1)\)、\(\mathrm{B}(2, 2)\)、\(\mathrm{C}(3, −2)\) を頂点にもつ \(\triangle \mathrm{ABC}\) の面積を求めよ。

いろいろな求め方ができますが、ここでは点と直線の距離を使った求め方を示します。
底辺と見る直線と、高さをなす頂点を決め、三角形の面積の公式 \(S = \displaystyle \frac{1}{2}(\text{底辺})(\text{高さ})\) を用います。
このときの高さを、点と直線の距離で求めることができますね。
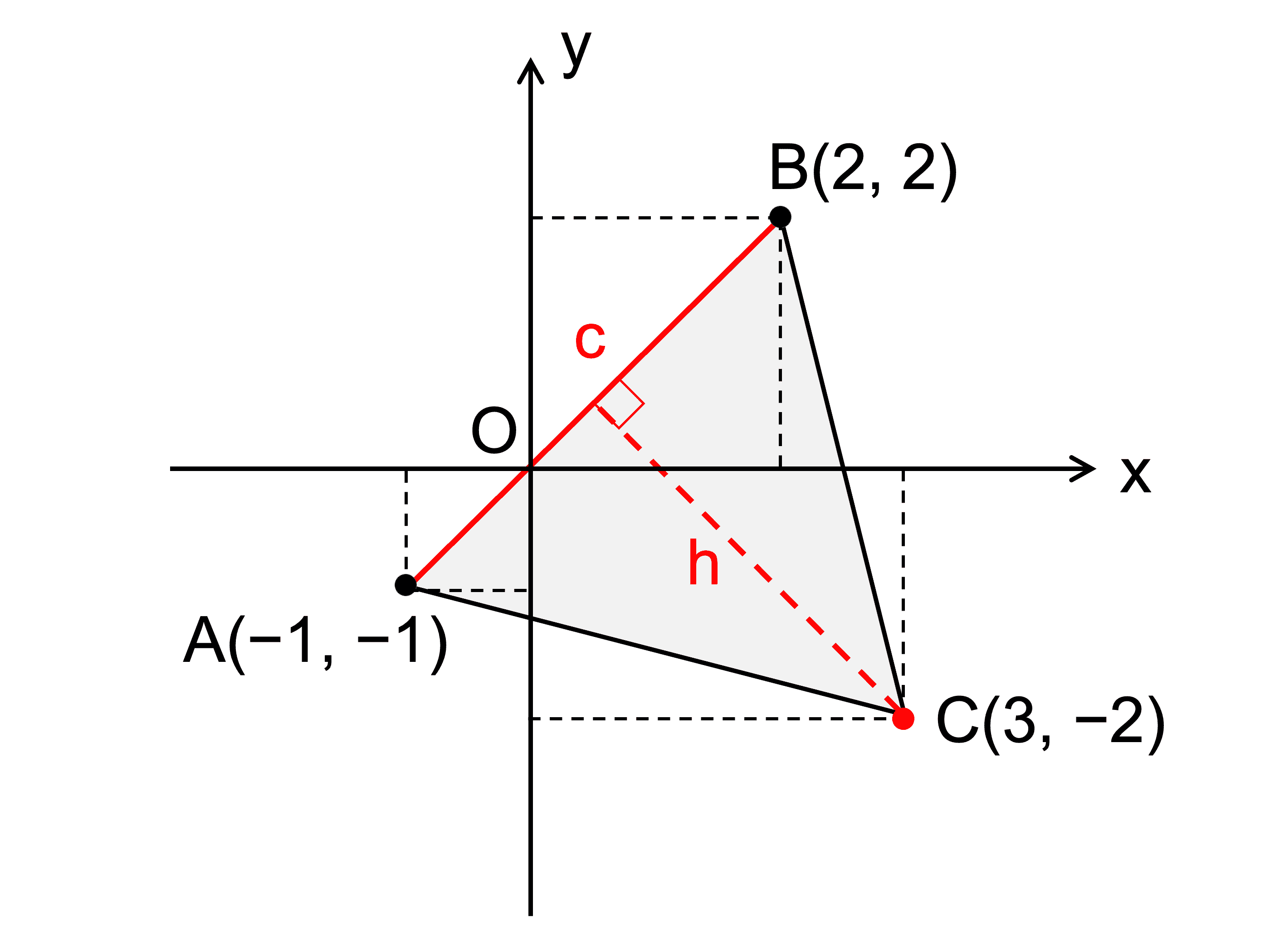
線分 \(\mathrm{AB}\) の長さ \(c\)、すなわち \(2\) 点 \(\mathrm{A}(−1, −1)\)、\(\mathrm{B}(2, 2)\) の距離は
\(\begin{align}c &= \sqrt{\{2 − (−1)\}^2 + \{2 − (−1)\}^2} \\&= \sqrt{3^2 + 3^2} \\&= \sqrt{18} \\&= 3\sqrt{2}\end{align}\)
また、直線 \(\mathrm{AB}\) の方程式は
\(y − (−1) = \displaystyle \frac{2 − (−1)}{2 − (−1)}\{x − (−1)\}\)
\(y + 1 = \displaystyle \frac{3}{3}(x + 1)\)
\(y + 1 = x + 1\)
\(x − y = 0\)
頂点 \(\mathrm{C}(3, −2)\) から直線 \(\mathrm{AB}\) : \(x − y = 0\) に引いた垂線の長さ \(h\) は
\(\begin{align}h &= \displaystyle \frac{|1 \cdot 3 + (−1) \cdot (−2)|}{\sqrt{1^2 + (−1)^2}} \\&= \displaystyle \frac{|3 + 2|}{\sqrt{1 + 1}} \\&= \displaystyle \frac{|5|}{\sqrt{2}} \\&= \displaystyle \frac{5\sqrt{2}}{2}\end{align}\)
\(\triangle \mathrm{ABC}\) の面積 \(S\) は
\(\begin{align}S &= \displaystyle \frac{1}{2}ch \\&= \displaystyle \frac{1}{2} \cdot 3\sqrt{2} \cdot \frac{5\sqrt{2}}{2}\\&= \displaystyle \frac{3 \cdot 5 \cdot 2}{2 \cdot 2} = \displaystyle \frac{15}{2}\end{align}\)
答え: \(\color{red}{\displaystyle \frac{15}{2}}\)
いかがでしたか?
点と直線の距離は、公式が覚えにくいと感じるかもしれませんね。
問題の数をこなしていけば、パターンが分かってきてサクサク解けるようになりますよ!


