この記事では、「二項分布」についてわかりやすく解説します。
期待値(平均)・分散・標準偏差の公式や、確率を求める計算問題、正規分布による近似についても説明しますので、ぜひこの記事を通してマスターしてくださいね!
目次
二項分布とは?
二項分布とは、\(1\) 回の試行で結果が \(2\) 通りしかない(ある事象が「起こる」か「起こらない」かなど)場合に、この試行を繰り返した時の確率分布のことです。
ある試行で事象 \(A\) が起こる確率を \(p\)、起こらない確率を \(q = (1 − p)\) とする。
この試行を \(n\) 回行う反復試行において、事象 \(A\) が起こる回数を \(X\) とすると、\(X\) は確率変数であり、その確率分布を二項分布といい、\(B(n, p)\) で表す。
\(n\) 回の試行で \(A\) がちょうど \(k\) 回起こる確率は
\begin{align}P(X = k) = {}_n \mathrm{C}_k p^kq^{n − k}\end{align}
であるから、\(X\) の確率分布は次のようになる。

二項分布の計算の前提となる「反復試行の確率」については、以下の記事で詳しく説明しています。
 反復試行の確率・独立試行の確率とは?公式や見分け方
反復試行の確率・独立試行の確率とは?公式や見分け方
ベルヌーイ試行の反復 → 二項分布
二項分布で扱う、\(1\) 回の試行で結果が \(2\) 通りしかない試行を「ベルヌーイ試行」といいます。
ただし、ベルヌーイ試行は次の条件を満たす必要があります。
- 各試行が独立である(前の試行の結果に左右されない)
- 確率 \(p\) および \((1 − p)\) がどの試行でも一定である
二項分布の例とイメージ
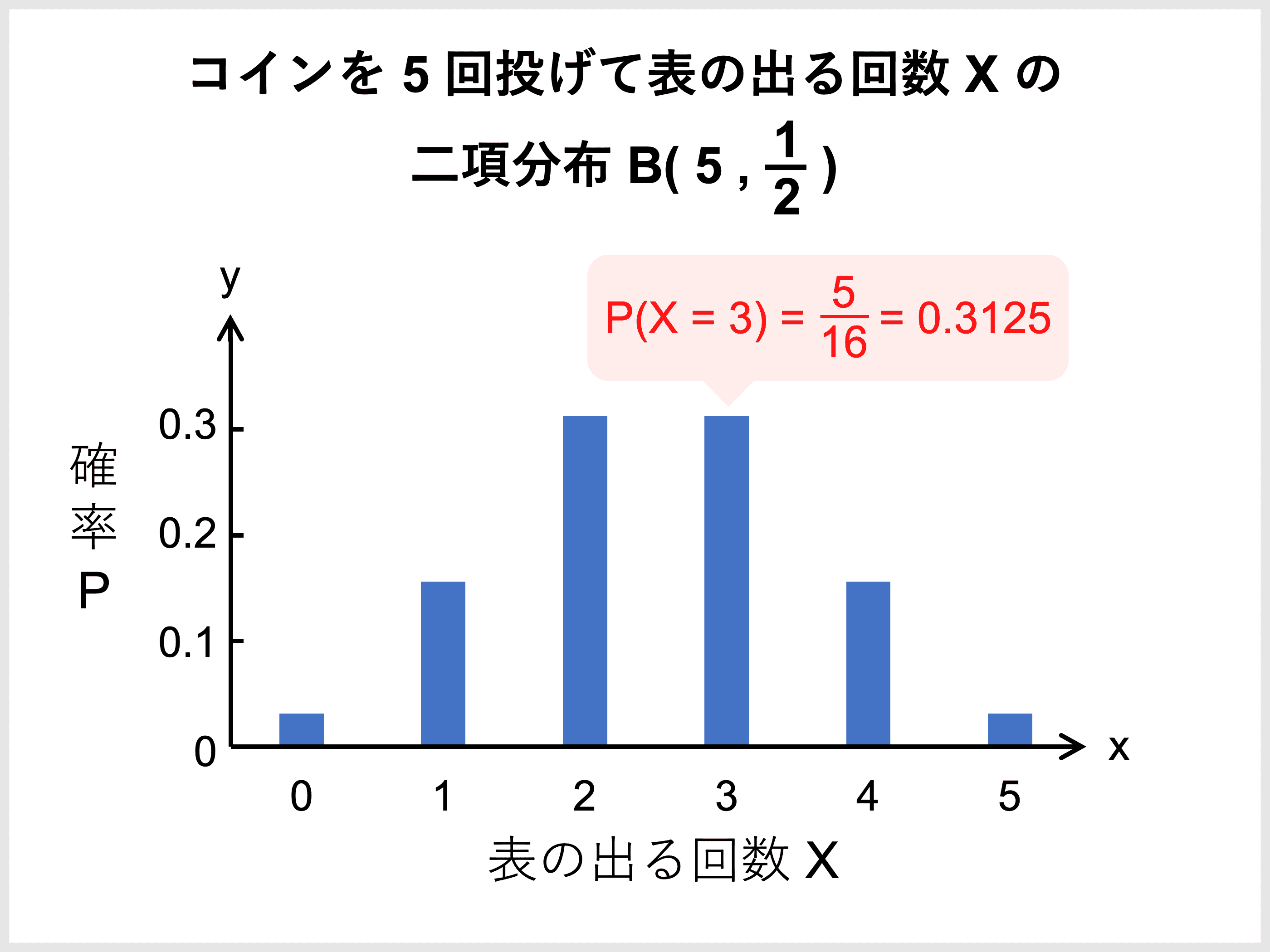
例えば、「コインを \(5\) 回投げて表が \(3\) 回出る確率」を知りたいときに、二項分布を活用できます。
コインを投げた結果は、「表が出る」か「裏が出るか」の \(2\) 通りですから、ベルヌーイ試行といえますね。
状況を整理すると、次のようになります。
- 試行:コインを投げる
- 注目する事象 :表が出る
- 確率変数 \(X\):表が出る回数
- ある試行で表が出る確率 \(p\):\(\displaystyle \frac{1}{2}\)
- 試行回数 \(n\):\(5\) 回
よって、\(5\) 回の試行のうち、表が出る回数 \(X\) は二項分布 \(B\left(5, \displaystyle \frac{1}{2}\right)\) に従います。
したがって、「コインを \(5\) 回投げて表が \(3\) 回出る確率 \(P(X = 3)\)」は次のように求められます。
\(\begin{align}P(X = 3) &= {}_5 \mathrm{C}_3 \left(\displaystyle \frac{1}{2}\right)^3 \left(1 − \frac{1}{2}\right)^{5 − 3} \\&= {}_5 \mathrm{C}_3 \left(\displaystyle \frac{1}{2}\right)^3 \left(\frac{1}{2}\right)^2\\&= {}_5 \mathrm{C}_2 \left(\displaystyle \frac{1}{2}\right)^5\\&= \displaystyle \frac{5 \cdot 4}{2 \cdot 1} \left(\displaystyle \frac{1}{2}\right)^5\\&= \displaystyle 10 \cdot \frac{1}{32}\\&= \color{red}{\displaystyle \frac{5}{16}}\end{align}\)
ちなみに、この二項分布 \(B\left(5, \displaystyle \frac{1}{2}\right)\) をグラフで表すと次のようになります。
二項分布の期待値・分散・標準偏差の公式
ここでは、二項分布の重要な公式を示します。
確率変数 \(X\) が二項分布 \(B(n, p)\) に従うとき、\(q = 1 − p\) とおくと
- 期待値(平均)
\begin{align}E(X) = np\end{align} - 分散
\begin{align}V(X) = npq\end{align} - 標準偏差
\begin{align}\sigma(X) = \sqrt{npq}\end{align}
二項分布なら上記公式に従って簡単に計算できるので、しっかり覚えておきましょう!
上記公式は、目的の確率変数 \(X\) を、各回の確率変数 \(X_i\) の和ととらえて求められます。
確率変数 \(X\) が二項分布 \(B(n, p)\) に従うとする。
\(1\) 回の試行で注目する事象が起こる確率は \(p\)、起こらない確率は \(q = 1 − p\) である。
\(i\) 回目(\(i = 1, 2, \cdots, n\))の試行で注目する事象が起こる回数を確率変数 \(X_i\) とおくと、その事象が起これば \(X_i = 1\)、起こらなければ \(X_i = 0\) であるから、
|
\(X_i\) |
\(1\) |
\(0\) |
|
\(P_i\) |
\(p\) |
\(q\) |
このとき、\(X_i\) の期待値 \(E(X_i)\) および分散 \(V(X_i)\) は
\(E(X_i) = 1 \cdot p + 0 \cdot q = p\)
\(\begin{align}V(X_i) &= E(X_i^2) − \{E(X_i)\}^2\\&= (1^2 \cdot p + 0^2 \cdot q) − p^2\\&= p − p^2\\&= p(1 − p)\\&= pq\end{align}\)
ここで、確率変数 \(X\) はこの試行を \(n\) 回繰り返した際に注目する事象が起こる回数であるから、
\(X = X_1 + X_2 + \cdots + X_n\)
とおける。
よって \(X\) の期待値 \(E(X)\) は
\(\begin{align}E(X) &= E(X_1 + X_2 + \cdots + X_n)\\&= E(X_1) + E(X_2) + \cdots + E(X_n)\\&= p + p + \cdots + p\\&= \color{red}{np}\end{align}\)
和の期待値の性質「\(E(X + Y) = E(X) + E(Y)\)」を利用
また、確率変数 \(X_1, X_2, \cdots, X_n\) は互いに独立であるから、
\(X\) の分散 \(V(X)\) は
\(\begin{align}V(X) &= V(X_1 + X_2 + \cdots + X_n)\\&= V(X_1) + V(X_2) + \cdots + V(X_n)\\&= pq + pq + \cdots + pq\\&= \color{red}{npq}\end{align}\)
和の分散の性質「\(X, Y\) が独立ならば \(V(X + Y) = V(X) + V(Y)\)」を利用
よって、\(X\) の標準偏差 \(\sigma(X)\) は
\(\sigma(X) = \sqrt{V(X)} = \color{red}{\sqrt{npq}}\)
(証明終わり)
二項分布の計算問題
それでは、二項分布の計算問題に挑戦してみましょう。
計算問題①「硬貨を投げる試行の \(E(X)\), \(V(X)\), \(\sigma(X)\)」
\(1\) 枚の硬貨を続けて \(5\) 回投げるとき、表が出る回数を \(X\) とする。\(X\) の期待値 \(E(X)\) と標準偏差 \(\sigma(X)\) を求めよ。また、\(P(X = 3)\) を求めよ。

表が出るか出ないかの \(2\) 通りなので、硬貨を投げる問題は典型的な二項分布ですね。
\(X\) が従う二項分布を明らかにして、\(E(X)\) と \(\sigma(X)\) を求めましょう。
\(X\) のとりうる値は \(X = 0, 1, 2, 3, 4, 5\)
\(1\) 回の試行で表が出る確率は \(\displaystyle \frac{1}{2}\) であるから、
\(X = r\) となる確率 \(P(X = r)\) は
\(P(X = r) = {}_5 \mathrm{C}_r \left(\displaystyle \frac{1}{2}\right)^r\left(\displaystyle \frac{1}{2}\right)^{5 − r}\) \((r = 0, 1, 2, 3, 4, 5)\)
よって、確率変数 \(X\) は二項分布 \(B\left(5, \displaystyle \frac{1}{2}\right)\) に従うから
\(E(X) = 5 \cdot \displaystyle \frac{1}{2} = \displaystyle \frac{5}{2}\)
\(\sigma(X) = \sqrt{5 \cdot \displaystyle \frac{1}{2} \cdot \frac{1}{2}} = \displaystyle \frac{\sqrt{5}}{2}\)
また、
\(\begin{align}P(X = 3) &= {}_5 \mathrm{C}_3 \left(\displaystyle \frac{1}{2}\right)^3\left(\frac{1}{2}\right)^{5 − 3} \\&= \displaystyle \frac{5 \cdot 4}{2 \cdot 1} \cdot \displaystyle \frac{1}{2^5}\\&= \displaystyle \frac{5}{16}\end{align}\)
答え:
\(E(X) = \displaystyle \frac{5}{2}\)、\(\sigma(X) = \displaystyle \frac{\sqrt{5}}{2}\)
\(P(X = 3) = \displaystyle \frac{5}{16}\)
計算問題②「サイコロと点の移動の二項分布」
数直線上で点 \(P\) が原点の位置にある。サイコロを投げて \(5\) 以上の目が出たら \(+2\) だけ進み、\(4\) 以下の目が出たら \(+1\) だけ進む。サイコロを \(3\) 回続けて投げるとき、\(P\) の座標 \(X\) の期待値と分散を求めよ。

「\(5\) 以上の目になる」か「\(4\) 以下の目になるか」の \(2\) 通りなので、二項分布に従うはずです。
「\(5\) 以上の目になる」回数を確率変数ととらえ、これを利用して \(X\) の期待値・分散を求めましょう。
サイコロを \(3\) 回投げたうち、\(5\) 以上の目が \(Y\) 回出たとすると、そのときの座標 \(X\) は
\(X = (+2)Y + (+1)(3 − Y) = Y + 3\)
サイコロを \(1\) 回投げて \(5\) 以上の目が出る確率は
\(\displaystyle \frac{2}{6} = \displaystyle \frac{1}{3}\)
よって、確率変数 \(Y\) は二項分布 \(B\left(3, \displaystyle \frac{1}{3}\right)\) に従うから、
\(E(Y) = 3 \cdot \displaystyle \frac{1}{3} = 1\)
\(V(Y) = 3 \cdot \displaystyle \frac{1}{3} \cdot \displaystyle \frac{2}{3} = \displaystyle \frac{2}{3}\)
したがって、\(X\) の期待値および分散は
\(E(X) = E(Y + 3) = E(Y) + 3 = 4\)
\(V(X) = V(Y + 3) = 1^2V(Y) = \displaystyle \frac{2}{3}\)
答え: \(E(X) = 4\)、\(V(X) = \displaystyle \frac{2}{3}\)
計算問題③「二項分布に従う確率の比」
平均値が \(6\)、分散が \(2\) の二項分布に従う確率変数を \(X\) とする。
\(X = k\) となる確率を \(P_k\) とおく。\(\displaystyle \frac{P_4}{P_3}\) の値を求めよ。

確率変数 \(X\) の平均 \(E(X)\) と分散 \(V(X)\) がわかっている問題です。
\(X\) が従う二項分布の試行回数 \(n\) と確率 \(p\) を明らかにしましょう。
\(X\) が従う二項分布を \(B(n, p)\) とおくと、平均値が \(6\)、分散が \(2\) であるから
\(\left\{\begin{array}{l} np = 6 \cdots ①\\ np(1 − p) = 2 \cdots ②\end{array}\right.\)
①を②に代入して
\(6(1 − p) = 2\)
\(1 − p = \displaystyle \frac{1}{3}\)
よって \(p = \displaystyle \frac{2}{3}\)
①より \(n = \displaystyle \frac{6}{p} = \displaystyle \frac{6 \cdot 2}{3} = 9\)
また、
\(P_k = P(X = k) = {}_n \mathrm{C}_k p^k (1 − p)^{n − k}\)
であるから、
\(\begin{align}\displaystyle \frac{P_4}{P_3} &= \displaystyle \frac{{}_9 \mathrm{C}_4 p^4 (1 − p)^5}{{}_9 \mathrm{C}_3 p^3 (1 − p)^6} \\&= \displaystyle \frac{3p}{2(1 − p)} \\&= \displaystyle \frac{3 \cdot \frac{2}{3}}{2 \cdot \frac{1}{3}} \\&= 3\end{align}\)
答え: \(\displaystyle \frac{P_4}{P_3} = 3\)
二項分布の正規分布による近似
二項分布は、試行回数 \(n\) を大きくすると正規分布で近似できます。
二項分布 \(B(n, p)\) に従う確率変数 \(X\) は、\(n\) が十分に大きいとき、近似的に正規分布 \(N(np, npq)\) に従う。
さらに、\(Z = \displaystyle \frac{X − np}{\sqrt{npq}}\) とおくと、\(Z\) は標準正規分布 \(N(0, 1)\) に従う。
正規分布による近似の例とイメージ
実際の例を見てみましょう。
注目する事象が起こる確率 \(p = \displaystyle \frac{1}{5}\) である試行を考えます。
試行回数 \(n\) を \(5\) 回、\(10\) 回、\(100\) 回と増やしていくと、二項分布は次のようになります。

確かに、試行回数が増えるごとにグラフの形が左右対称な正規分布に近づいていきますね。
試行回数 \(n\) が増えれば増えるほどコンビネーション \({}_n \mathrm{C}_k\) の計算が大変になりますから、正規分布に近似して計算を楽にしよう!ということなのです。
正規分布に近似すれば、正規分布表から簡単に確率を求められます。
正規分布や正規分布表の使い方については、以下の記事で詳しく説明しています。
 正規分布とは?表の見方や計算問題をわかりやすく解説!
正規分布とは?表の見方や計算問題をわかりやすく解説!
練習問題「サイコロを投げる反復試行」
実際に、二項分布を正規分布で近似する問題を見てみましょう。
\(1\) 個のサイコロを \(360\) 回投げるとき、\(3\) の目の出る回数を \(X\) とする。\(X\) が次の範囲の値をとる確率を求めよ。
(1) \(50 \leq X \leq 60\)
(2) \(\left|\displaystyle \frac{X}{360} − \frac{1}{6}\right| \leq 0.05\)

特定の目が「出るか」「出ないか」の \(2\) 通りの結果をもつ試行なので、確率変数 \(X\) は二項分布に従います。
試行回数が多いので、二項分布を正規分布で近似できますね。
\(X\) は二項分布 \(B\left(360, \displaystyle \frac{1}{6}\right)\) に従うので、\(X\) の期待値 \(m\) および標準偏差 \(\sigma\) は
\(m = 360 \cdot \displaystyle \frac{1}{6} = 60\)
\(\sigma = \sqrt{360 \cdot \displaystyle \frac{1}{6} \cdot \frac{5}{6}} = \sqrt{50} = 5\sqrt{2}\)
\(n = 360\) は十分大きいから、\(X\) は近似的に正規分布 \(N(60, (5\sqrt{2})^2)\) に従う。
よって \(Z = \displaystyle \frac{X − 60}{5\sqrt{2}}\) とおくと、\(Z\) は近似的に標準正規分布 \(N(0, 1)\) に従う。
(1)
\(P(50 \leq X \leq 60)\)
\(= P\left(\displaystyle \frac{50 − 60}{5\sqrt{2}} \leq Z \leq \displaystyle \frac{60 − 60}{5\sqrt{2}}\right)\)
\(= P(−\sqrt{2} \leq Z \leq 0)\)
\(= p(\sqrt{2})\)
\(≒ p(1.41)\)
\(= 0.4207\)
答え: \(0.4207\)
(2)
\(P\left(\left|\displaystyle \frac{X}{360} − \frac{1}{6}\right| \leq 0.05\right)\)
\(= P(|X − 60| \leq 18)\)
\(= P\left(|Z| \leq \displaystyle \frac{18}{5\sqrt{2}}\right)\)
\(= 2p\left(\displaystyle \frac{18}{5\sqrt{2}}\right)\)
\(≒ 2p(2.55)\)
\(= 2 \cdot 0.4946\)
\(= 0.9892\)
答え: \(0.9892\)
以上で問題も終わりです!
二項分布は比較的理解しやすく、計算も難しくないです。
この記事を通して、ぜひマスターしてくださいね!
