この記事では、「三角関数の合成」の公式や証明、実際のやり方をわかりやすく解説していきます。
角度の範囲に応じて三角関数の最大・最小を求める問題や、グラフを書く問題も紹介しますので、ぜひ合成をマスターしてくださいね。
目次
三角関数の合成とは?
三角関数の合成とは、sin と cos の和で表された式を、sin だけ、または cos だけの式に変形することです。
最もよく使うのは、sin だけの式に変形する次の公式です。
三角関数の合成の公式(sin 型)
\(a \neq 0\), \(b \neq 0\) のとき、
\begin{align}\color{red}{a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha)}\end{align}
ただし、\(\alpha\) は
\(\displaystyle \cos\alpha = \frac{a}{\sqrt{a^2 + b^2}}\)、\(\displaystyle \sin\alpha = \frac{b}{\sqrt{a^2 + b^2}}\) を満たす角

三角関数の合成の公式(cos 型)
三角関数の合成は \(\sin\) 型の公式が一般的ですが、\(\cos\) にも合成できます。
\(a \neq 0\), \(b \neq 0\) のとき、
\begin{align}\color{red}{\displaystyle a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \cos(\theta − \beta)}\end{align}
ただし、\(\beta\) は
\(\displaystyle \cos\beta = \frac{b}{\sqrt{a^2 + b^2}}\)、\(\displaystyle \sin\beta = \frac{a}{\sqrt{a^2 + b^2}}\) を満たす角
三角関数の合成の証明
三角関数の合成公式の証明を示します。合成公式は暗記が必須なので、証明方法を理解して定着させましょう。
\(a \neq 0\), \(b \neq 0\) のとき、以下の式を証明せよ。
\begin{align}a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha)\end{align}
(ただし、\(\alpha\) は \(\displaystyle \cos\alpha = \frac{a}{\sqrt{a^2 + b^2}}\)、\(\displaystyle \sin\alpha = \frac{b}{\sqrt{a^2 + b^2}}\) を満たす角)
三角関数の合成は、実は加法定理の逆です。
\(\sin\) の加法定理を使って式変形することで、三角関数の合成公式を証明できます。
sin の加法定理
\begin{align}\sin(\alpha + \beta) = \sin\alpha \cos\beta + \cos\alpha \sin\beta\end{align}
\(xy\) 平面に点 \(\mathrm{P}(a, b)\) をとり、\(\mathrm{OP} = r\) とおく。

\(\mathrm{OP}\) が \(x\) 軸の正の向きとなす角を \(\alpha\) とすると、
\(\displaystyle \cos\alpha = \frac{a}{r}\) より、\(a = r \cos\alpha\) …①
\(\displaystyle \sin\alpha = \frac{b}{r}\) より、\(b = r \sin\alpha\) …②
三平方の定理より \(r = \sqrt{a^2 + b^2}\) …③
これを \(a \sin\theta + b \cos\theta\) に代入すると、
\(a \sin\theta + b \cos\theta\)
\(= r \cos\alpha \sin\theta + r \sin\alpha \cos\theta\)(①、②代入)
\(= r(\sin\theta \cos\alpha + \cos\theta \sin\alpha)\)
\(= r \sin(\theta + \alpha)\)(sin の加法定理)
\(= \sqrt{a^2 + b^2} \sin(\theta + \alpha)\)(③代入)
したがって、
\(a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha)\)
が成り立つ。
ただし、
\(\left\{\begin{array}{l} \cos\alpha = \displaystyle \frac{a}{r} = \frac{a}{\sqrt{a^2 + b^2}}\\ \sin\alpha = \displaystyle \frac{b}{r} = \frac{b}{\sqrt{a^2 + b^2}}\end{array}\right.\)
(証明終わり)
\(\cos\) への合成公式も、\(\cos\) の加法定理を利用して同様に導けます。
自分で証明してみると、より理解が深まりますよ。
三角関数の合成のやり方【例題】
次の例題を通して、三角関数の合成のやり方を説明します。
次の三角関数を合成せよ。
\(\sin\theta − \cos\theta\)
「式変形によるやり方」と「図を使ったやり方」の \(2\) 通りの手順を示します。
やり方① 式変形
証明と同じ流れで、\(\sin\) の加法定理が使えるように式を変形していきます。
まずは、\(a\sin\theta + b\cos\theta\) の係数部分に注目して \(\sqrt{a^2 + b^2}\) を計算し、その値で式全体をくくります。
例題の \(\sin\theta − \cos\theta\) では、\(a = 1\), \(b = −1\) ですね。
\(\sqrt{1^2 + (−1)^2} = \sqrt{2}\) より
\(\sin\theta − \cos\theta\)
\(\displaystyle = \sqrt{2} \left( \frac{1}{\sqrt{2}} \sin\theta − \frac{1}{\sqrt{2}} \cos\theta \right)\)
ここで、\(\sin\) の項にかかる係数が \(\cos \alpha\)、 \(\cos\) の項にかかる係数が \(\sin \alpha\) となるような角度 \(\alpha\) を探します。
例題では、\(\cos \alpha = \displaystyle \frac{1}{\sqrt{2}}\)、\(\sin \alpha = \displaystyle −\frac{1}{\sqrt{2}}\) となるような角度 \(\alpha\) を探せばよいですね。
必要であれば単位円を書いて調べます。
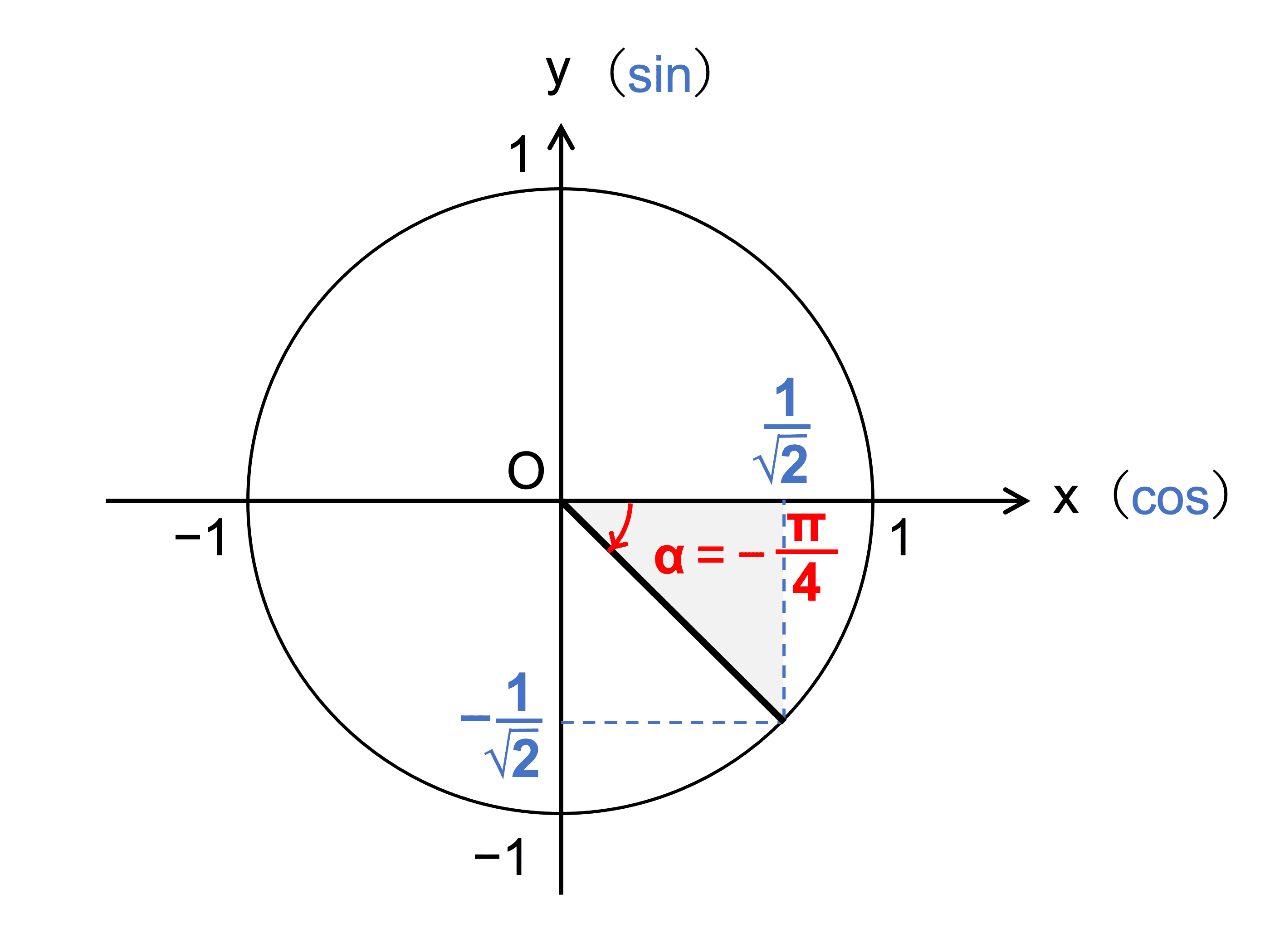
\(\displaystyle \frac{1}{\sqrt{2}} = \cos \left( −\frac{\pi}{4} \right)\)、\(\displaystyle −\frac{1}{\sqrt{2}} = \sin \left( −\frac{\pi}{4} \right)\)
係数部分を STEP.2 で特定した三角比に書き換え、加法定理の右辺 \(\sin(\alpha + \beta) = \underline{\sin\alpha \cos\beta + \cos\alpha \sin\beta}\) の形になるように式を整理します。
\(\sin\theta − \cos\theta\)
\(= \displaystyle \sqrt{2} \left( \frac{1}{\sqrt{2}} \sin\theta − \frac{1}{\sqrt{2}} \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \cos \left( −\frac{\pi}{4} \right) \sin\theta + \sin \left( −\frac{\pi}{4} \right) \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \underline{\sin\theta \cos \left( −\frac{\pi}{4} \right) + \cos\theta \sin \left( −\frac{\pi}{4} \right) }\right)\)
ここで、加法定理を逆向きに使って \(\sin\) に合成します。
(\(\sin(\alpha + \beta) ← \sin\alpha \cos\beta + \cos\alpha \sin\beta\))
\(\sin\theta − \cos\theta\)
\(= \displaystyle \sqrt{2} \left( \frac{1}{\sqrt{2}} \sin\theta − \frac{1}{\sqrt{2}} \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \cos \left( −\frac{\pi}{4} \right) \sin\theta + \sin \left( −\frac{\pi}{4} \right) \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \sin\theta \cos \left( −\frac{\pi}{4} \right) + \cos\theta \sin \left( −\frac{\pi}{4} \right) \right)\)
\(\displaystyle = \sqrt{2} \sin \left( \theta − \frac{\pi}{4} \right)\)
したがって、\(\color{red}{\displaystyle \sin\theta − \cos\theta = \sqrt{2} \sin \left( \theta − \frac{\pi}{4} \right)}\) と合成できました!
実際の解答に書くのは、式変形の部分だけで大丈夫です。慣れてくると STEP.1、STEP.2 は暗算でもできるようになりますよ。
\(\sin\theta − \cos\theta\)
\(= \displaystyle \sqrt{2} \left( \frac{1}{\sqrt{2}} \sin\theta − \frac{1}{\sqrt{2}} \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \cos \left( −\frac{\pi}{4} \right) \sin\theta + \sin \left( −\frac{\pi}{4} \right) \cos\theta \right)\)
\(\displaystyle = \sqrt{2} \left( \sin\theta \cos \left( −\frac{\pi}{4} \right) + \cos\theta \sin \left( −\frac{\pi}{4} \right) \right)\)
\(\displaystyle = \sqrt{2} \sin \left( \theta − \frac{\pi}{4} \right)\)
答え: \(\color{red}{\displaystyle \sqrt{2} \sin \left( \theta − \frac{\pi}{4} \right)}\)
やり方② 作図の利用
合成公式 \(a \sin\theta + b \cos\theta = \color{red}{\sqrt{a^2 + b^2}} \sin(\theta + \color{red}{\alpha})\) に当てはまるような \(\sqrt{a^2 + b^2}\) と \(\alpha\) の値を、座標平面から求める方法です。
なお、この方法が使えるのは sin 型の合成公式だけです。
\(xy\) 平面に点 \(\mathrm{P}(a, b)\) を取り、\(x\) 軸に垂線 \(\mathrm{PA}\) を下ろします。
例題 \(\sin\theta − \cos\theta\) では、\(a = 1\), \(b = −1\) ですね。
点 \(\mathrm{P}(1, −1)\) とおき、\(x\) 軸に下ろした垂線の足を点 \(\mathrm{A}(1, 0)\) とする。
原点 \(\mathrm{O}(0, 0)\) から \(\mathrm{P}(1, −1)\) までの距離 \(\sqrt{a^2 + b^2}\) を計算します。
\(\mathrm{OP} = \sqrt{1^2 + (−1)^2} = \sqrt{2}\)
直角三角形 \(\triangle \mathrm{OAP}\) の辺の比に注目して、\(\mathrm{OP}\) と \(x\) 軸のなす角 \(\alpha\) を求めます。
\(\triangle \mathrm{OAP}\) は \(1 : 1 : \sqrt{2}\) の直角三角形なので
\(\mathrm{OP}\) と \(x\) 軸のなす角 \(\alpha\) は
\(\displaystyle \alpha = −\frac{\pi}{4}\)

sin 型の合成公式 \(a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha)\) に、ここまでに求めた \(\sqrt{a^2 + b^2}\) と \(\alpha\) を代入すれば合成の完成です。
\(a \sin\theta + b \cos\theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha)\) より、
\(\color{red}{\displaystyle \sin\theta − \cos\theta = \sqrt{2} \sin \left( \theta − \frac{\pi}{4} \right)}\)
ここではていねいに文章でも説明しましたが、座標平面の図を書くだけでいいのでサクッと求められます。
三角関数の合成のやり方として、式変形と作図の \(2\) 通りを解説しました。
おそらく、慣れてしまえば作図の方が簡単だと思います。
ですが、式変形の方が三角関数の合成の本来の意味に従っているので、どちらも理解しておきましょう。
三角関数の合成の練習問題
それでは、三角関数の合成の練習問題を解きましょう。
練習問題「sinθ + √3cosθ を合成する」
次の三角関数を合成せよ。
\(\sin\theta + \sqrt{3} \cos\theta\)

①式変形による解答、②作図による解答のどちらも示します。
\(\sqrt{1^2 + (\sqrt{3})^2} = 2\) より、
\(\displaystyle \sin\theta + \sqrt{3} \cos\theta\)
\(\displaystyle = 2\left(\frac{1}{2}\sin\theta + \frac{\sqrt{3}}{2}\cos\theta \right)\)
\(\displaystyle = 2\left(\cos\frac{\pi}{3} \sin \theta + \sin\frac{\pi}{3} \cos \theta \right)\)
\(\displaystyle = 2\left(\sin \theta \cos\frac{\pi}{3} + \cos \theta \sin\frac{\pi}{3}\right)\)
\(\displaystyle = 2 \sin \left( \theta + \frac{\pi}{3} \right)\)
答え: \(\displaystyle 2 \sin \left( \theta + \frac{\pi}{3} \right)\)
\(\mathrm{P}(1, \sqrt{3})\) とおくと、
\(\mathrm{OP} = \sqrt{1^2 + (\sqrt{3})^2} = 2\)
\(\mathrm{OP}\)と \(x\) 軸とのなす角 \(\alpha\) は \(\displaystyle \alpha = \frac{\pi}{3}\)

よって、
\(\displaystyle \sin\theta + \sqrt{3} \cos\theta = 2 \sin \left( \theta + \frac{\pi}{3} \right)\)
答え: \(\displaystyle 2 \sin \left( \theta + \frac{\pi}{3} \right)\)
三角関数の合成の応用問題
最後に、三角関数の合成の応用問題に挑戦してみましょう。
応用問題①「最大値、最小値を求める」
\(0 \leq \theta \leq \pi\) のとき、\(f(\theta) = 2 \sin\theta + 3 \cos\theta\) の最大値、最小値を求めよ。

まずは三角関数を合成して、求める式の三角比を \(1\) つに統一します。
最大・最小の問題では、角度や三角比のとりうる値の範囲に必ず気を配りましょう。
角度 \(\theta\) の範囲から合成後の角度 \(\theta + \alpha\) の範囲、関数 \(f(\theta)\) のとりうる値の範囲を順番に求めるのがポイントです。
\(\sqrt{2^2 + 3^2} = \sqrt{13}\) より、
\(\begin{align} f(\theta) &= 2 \sin\theta + 3 \cos\theta \\ &= \sqrt{13} \left( \frac{2}{\sqrt{13}} \sin\theta + \frac{3}{\sqrt{13}} \cos\theta \right) \\ &= \sqrt{13} (\cos\alpha \sin\theta + \sin\alpha \cos\theta) \\ &= \sqrt{13} \sin(\theta + \alpha) \end{align}\)
(ただし、 \(\alpha\) は \(\displaystyle \sin\alpha = \frac{3}{\sqrt{13}}\)、\(\displaystyle \cos\alpha = \frac{2}{\sqrt{13}}\) を満たす角)
\(0 \leq \theta \leq \pi\) より、
\(\alpha \leq \theta + \alpha \leq \pi + \alpha\)
このとき、図のように \(\sin(\theta + \alpha)\) のとる範囲は
\(\displaystyle −\frac{3}{\sqrt{13}} \leq \sin(\theta + \alpha) \leq 1\)

よって、\(\sin(\theta + \alpha)\) は
- \(\displaystyle \theta + \alpha = \frac{\pi}{2}\) すなわち \(\displaystyle \theta = \frac{\pi}{2} − \alpha\) のとき
最大値 \(1\) - \(\theta + \alpha = \pi + \alpha\) すなわち \(\theta = \pi\) のとき
最小値 \(\displaystyle −\frac{3}{\sqrt{13}}\)
したがって、
\(f(\theta) = \sqrt{13} \sin(\theta + \alpha)\) \((0 \leq \theta \leq \pi)\) は、
- 最大値 \(\displaystyle f \left( \frac{\pi}{2} − \alpha \right) = \sqrt{13} \cdot 1 = \sqrt{13}\)
- 最小値 \(\displaystyle f(\pi) = \sqrt{13} \left( −\frac{3}{\sqrt{13}} \right) = −3\)
をとる。
答え:
\(\displaystyle \theta = \frac{\pi}{2} − \alpha\) のとき、最大値 \(\sqrt{13}\)
\(\theta = \pi\) のとき、最小値 \(−3\)
(ただし、\(\alpha\) は \(\displaystyle \sin\alpha = \frac{3}{\sqrt{13}}\)、\(\displaystyle \cos\alpha = \frac{2}{\sqrt{13}}\) を満たす角)
応用問題②「y = sin x + cos x のグラフを書く」
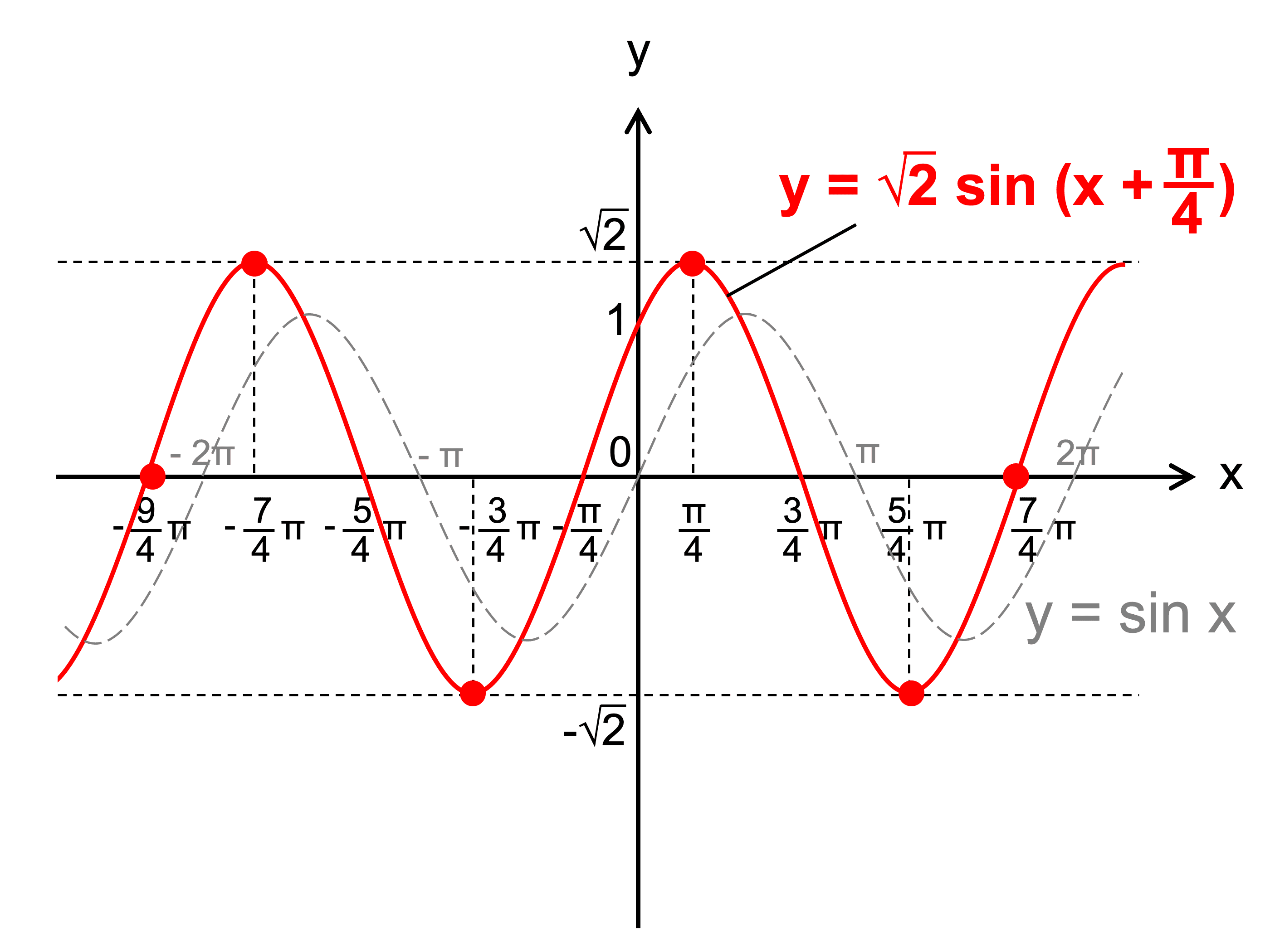
\(y = \sin x + \cos x\) のグラフを書け。

まずは三角関数を合成して、\(\sin\) だけの式に変換します。
そのあと、\(y = \sin x\) のグラフを基準に拡大縮小したり、平行移動したりして目的のグラフを得ましょう。
\(\sqrt{1^2 + 1^2} = \sqrt{2}\) より、
\(\begin{align} y &= \sin x + \cos x \\ &= \sqrt{2} \left( \frac{1}{\sqrt{2}} \sin x + \frac{1}{\sqrt{2}} \cos x \right) \\ &= \sqrt{2} \left( \cos \frac{\pi}{4} \sin x + \sin \frac{\pi}{4} \cos x \right) \\ &= \sqrt{2} \sin \left( x + \frac{\pi}{4} \right) \end{align}\)
\(\displaystyle y = \sqrt{2} \sin \left( x + \frac{\pi}{4} \right)\) のグラフは、
\(y = \sin x\) をもとにして、\(y\) 軸方向に \(\sqrt{2}\) 倍し、\(x\) 軸方向に \(\displaystyle −\frac{\pi}{4}\) だけ平行移動したものである。
したがってグラフは次のようになる。
答え:
以上で応用問題も終わりです!
三角関数の合成は、式変形・作図の考え方ともに理解しておきましょう。
合成ができないと次に進めない問題もたくさんあるので、しっかりとマスターしてくださいね!


