この記事では、「加法定理」についてできるだけわかりやすく解説していきます。
加法定理の語呂合わせによる覚え方や証明方法、応用問題の解き方も説明していくので、この記事を通してぜひマスターしてくださいね。
目次
加法定理とは?
加法定理とは、\(2\) つの角度の和や差 (\(\alpha \pm \beta\)) の三角関数を、個々の角度 \(\alpha, \beta\) の三角関数を用いて表現できることを示した定理です。
任意の実数 \(\alpha\), \(\beta\) に対して、以下の等式が成り立つ。
- 正弦(sin)
\(\color{red}{\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta}\)
\(\color{red}{\sin (\alpha − \beta) = \sin \alpha \cos \beta − \cos \alpha \sin \beta}\) - 余弦(cos)
\(\color{red}{\cos (\alpha + \beta) = \cos \alpha \cos \beta − \sin \alpha \sin \beta}\)
\(\color{red}{\cos (\alpha − \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta}\) - 正接(tan)
\(\color{red}{\displaystyle \tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 − \tan \alpha \tan \beta}}\)
\(\color{red}{\displaystyle \tan (\alpha − \beta) = \frac{\tan \alpha − \tan \beta}{1 + \tan \alpha \tan \beta}}\)
加法定理は三角関数の計算において欠かせないツールであるだけでなく、三角関数に関する公式のほとんどを導くことができる重要な定理です(→ 【補足】加法定理から導ける公式)。
以降、加法定理の覚え方や証明、使い方を順番に説明していきます。
加法定理の覚え方
ここでは、加法定理の語呂合わせによる覚え方を紹介します。
なお、どれも角度の和 (\(\alpha + \beta\)) の加法定理の語呂合わせとして覚えます。
和の加法定理の符号をすべて逆転させると、差の加法定理 (\(\alpha − \beta\)) が得られます。
sin の加法定理の語呂合わせ
咲いたコスモス コスモス咲いた
\(\sin (\alpha + \beta) = \color{skyblue}{\sin \alpha} \color{limegreen}{\cos \beta} + \color{limegreen}{\cos \alpha} \color{skyblue}{\sin \beta}\)
sin の加法定理は、左辺と右辺の符号がそろっていることも把握しておきましょう!
cos の加法定理の語呂合わせ
コスモスコスモス 咲かない咲かない
\(\cos (\alpha + \beta) = \color{limegreen}{\cos \alpha \cos \beta} \color{salmon}{−} \color{skyblue}{\sin \alpha \sin \beta}\)
「咲かない」が、符号が \(\bf{−}\) であることを意味しています。
sin と cos の語呂が似ていて混乱する人は、はじめの音が合う方と覚えておきましょう。
「さいたコスモス…」→ sin の加法定理
「コスモスコスモス…」→ cos の加法定理
tan の加法定理の語呂合わせ
イチ引くタンタン タン加タン
\(\displaystyle \tan (\alpha + \beta) = \frac{\color{orange}{\tan \alpha} \color{salmon}{+} \color{orange}{\tan \beta}}{\color{salmon}{1 −} \color{orange}{\tan \alpha \tan \beta}}\)
分母 → 分子の順番です。リズム感で覚えましょう!
tan の加法定理は、sin と cos の加法定理から簡単に導くこともできます。
(→ ③ tan の加法定理の証明 を参照)
語呂自体忘れた…という場合は、この方法で思い出してもいいかもしれませんね。
加法定理は覚えられそうでしょうか?
ここで紹介した語呂合わせはあくまでも一例です。
もっとしっくりくる語呂を探したり、自分で覚えやすいものを作ったりするのもオススメですよ!
加法定理の証明
加法定理の証明手順をわかりやすく説明します。
加法定理は、① cos → ② sin → ③ tan の順に証明できます。
① cos の加法定理の証明
cos の加法定理はいくつかの方法で証明できますが、ここでは点の回転移動と \(2\) 点間の距離の計算による方法を示します。
単位円周上に \(0^\circ\) の動径を示す点 \(\mathrm{P}\) と角 \(\alpha + \beta\) の動径を示す点 \(\mathrm{Q}\) をとり、これらを同じ角度 \(−\beta\) だけ回転移動しても \(2\) 点間の距離が変わらないことを利用して、\(\cos (\alpha + \beta)\) を導きます。
- 二点間の距離
\(2\) 点 \(\mathrm{A}(x_1, y_1)\), \(\mathrm{B}(x_2, y_2)\) の距離は
\begin{align}\mathrm{AB} = \sqrt{(x_2 − x_1)^2 + (y_2 − y_1)^2}\end{align} - 三角関数の角度の変換公式(負角)
\begin{align}\sin (−\theta) &= −\sin \theta \\ \cos (−\theta) &= \cos \theta\end{align}
(見切れる場合は横へスクロール)
単位円周上に
\(\mathrm{P}(1, 0)\)、\(\mathrm{Q}(\cos (\alpha + \beta)\), \(\sin (\alpha + \beta))\)
をとる。
この \(\mathrm{P}\), \(\mathrm{Q}\) を、原点を中心に \(−\beta\) だけ回転した点を \(\mathrm{P’}\), \(\mathrm{Q’}\) とおくと、
\(\mathrm{P’}(\cos (−\beta), \sin (−\beta))\)、\(\mathrm{Q’}(\cos \alpha, \sin \alpha)\)
で表される。
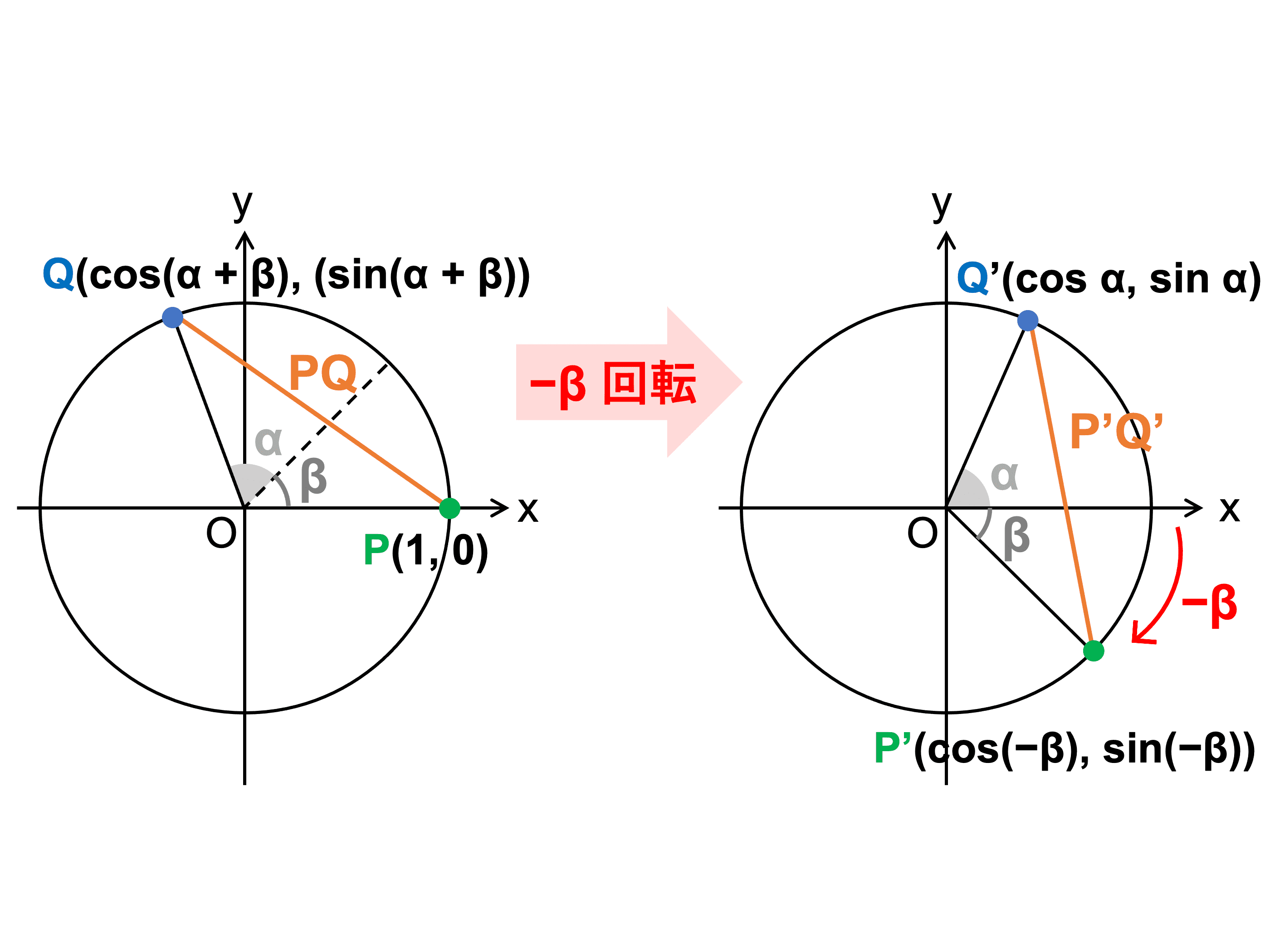
このとき、回転移動しても \(2\) 点間の距離は変わらないので
\(\mathrm{PQ} = \mathrm{P’Q’}\)
よって
\(\mathrm{PQ^2} = \mathrm{P’Q’^2}\)
ここで、
\(\mathrm{P}(1, 0)\)、\(\mathrm{Q}(\cos (\alpha + \beta), \sin (\alpha + \beta))\) より
\(\mathrm{PQ^2}\)
\(= \{1 − \cos (\alpha + \beta)\}^2 + \{0 − \sin (\alpha + \beta)\}^2\)
\(= \{1 − \cos (\alpha + \beta)\}^2 + \sin^2 (\alpha + \beta)\)
\(= 1 − 2\cos (\alpha + \beta) + \cos^2 (\alpha + \beta) + \sin^2 (\alpha + \beta)\)
\(= 1 − 2\cos (\alpha + \beta) + 1\)
\(= 2 − 2\cos (\alpha + \beta)\)
\(= 2(1 − \cos (\alpha + \beta))\) …①
\(\mathrm{P’}(\cos (−\beta), \sin (−\beta))\)、\(\mathrm{Q’}(\cos \alpha, \sin \alpha)\) より
\(\mathrm{P’Q’^2}\)
\(= \{\cos (−\beta) − \cos \alpha\}^2 + \{\sin (−\beta) − \sin \alpha\}^2\)
\(\cos (−\beta) = \cos \beta\), \(\sin (−\beta) = −\sin \beta\) より
\(\mathrm{P’Q’^2}\)
\(= (\cos \beta − \cos \alpha)^2 + (−\sin \beta − \sin \alpha)^2\)
\(= (\cos \beta − \cos \alpha)^2 + (\sin \beta + \sin \alpha)^2\)
\(= \cos^2 \beta − 2\cos \alpha \cos \beta + \cos^2 \alpha + \sin^2 \beta + 2\sin \alpha \sin \beta + \sin^2 \alpha\)
\(= (\sin^2 \beta + \cos^2 \beta) + (\sin^2 \alpha + \cos^2 \alpha) − 2\cos \alpha \cos \beta + 2\sin \alpha \sin \beta\)
\(= 2 − 2\cos \alpha \cos \beta + 2\sin \alpha \sin \beta\)
\(= 2(1 − \cos \alpha \cos \beta + \sin \alpha \sin \beta)\) …②
\(\mathrm{PQ^2} = \mathrm{P’Q’^2}\) に①、②を代入して
\(\begin{align}2(1 − &\cos (\alpha + \beta)) \\&= 2(1 − \cos \alpha \cos \beta + \sin \alpha \sin \beta)\end{align}\)
\(\begin{align}1 − \cos &(\alpha + \beta) \\&= 1 − \cos \alpha \cos \beta + \sin \alpha \sin \beta\end{align}\)
よって
\(\color{red}{\cos (\alpha + \beta) = \cos \alpha \cos \beta − \sin \alpha \sin \beta}\)
また、\(\beta\) を \(−\beta\) に置き換えると、
\(\cos (\alpha − \beta)\) \(= \cos \alpha \cos (−\beta) − \sin \alpha \sin (−\beta)\)
\(\cos (−\beta) = \cos \beta\), \(\sin (−\beta) = −\sin \beta\) より
\(\color{red}{\cos (\alpha − \beta)}\) \(\color{red}{= \cos \alpha \cos \beta + \sin \alpha \sin \beta}\)
以上より、cos の加法定理が成り立つ。
(証明終わり)
② sin の加法定理の証明
sin の加法定理は、三角関数の角度の変換公式を利用して cos の加法定理から導くことができます。
- cos の加法定理
\begin{align}\cos (\alpha − \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\end{align} - 三角関数の角度の変換公式(余角、負角)
\begin{align} \displaystyle &\sin \left( \frac{\pi}{2} − \theta \right) = \cos \theta\\ \displaystyle &\cos \left( \frac{\pi}{2} − \theta \right) = \sin \theta \\ &\sin (−\theta) = −\sin \theta \\ &\cos (−\theta) = \cos \theta\end{align}
\(\cos (\alpha − \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\) において、\(\alpha\) を \(\displaystyle \frac{\pi}{2} − \alpha\) に置き換えると、
\(\displaystyle \cos \left( \frac{\pi}{2} − \alpha − \beta \right)\) \(\displaystyle = \cos \left( \frac{\pi}{2} − \alpha \right) \cos\beta + \sin \left( \frac{\pi}{2} − \alpha \right) \sin \beta\)
すなわち、
\(\displaystyle \cos \left( \frac{\pi}{2} − (\alpha + \beta) \right)\) \(\displaystyle = \cos \left( \frac{\pi}{2} − \alpha \right) \cos\beta + \sin \left( \frac{\pi}{2} − \alpha \right) \sin \beta\)
ここで、
\(\displaystyle \cos \left( \frac{\pi}{2} − (\alpha + \beta) \right) = \sin (\alpha + \beta)\)、\(\displaystyle \cos \left( \frac{\pi}{2} − \alpha \right) = \sin \alpha\)、\(\displaystyle \sin \left( \frac{\pi}{2} − \alpha \right) = \cos \alpha\) より
\(\color{red}{\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta}\)
また、\(\beta\) を \(−\beta\) に置き換えると、
\(\sin (\alpha − \beta) = \sin \alpha \cos (−\beta) + \cos \alpha \sin (−\beta)\)
\(\cos (−\beta) = \cos \beta\)、\(\sin (−\beta) = −\sin \beta\) より
\(\color{red}{\sin (\alpha − \beta) = \sin \alpha \cos \beta − \cos \alpha \sin \beta}\)
以上より、sin の加法定理が成り立つ。
(証明終わり)
③ tan の加法定理の証明
三角比の相互関係に sin、cos の加法定理を代入すると、tan の加法定理を導けます。
- 三角比の相互関係
\begin{align}\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}\end{align} - sin、cos の加法定理
\begin{align}\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \cos (\alpha − \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\end{align} - 三角関数の角度の変換公式(負角)
\begin{align}\tan (−\theta) = −\tan \theta \end{align}
三角比の相互関係および sin、cos の加法定理から、
\(\begin{align}\displaystyle \tan (\alpha + \beta) &= \displaystyle \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)}\\& = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta − \sin \alpha \sin \beta}\end{align}\)
右辺の分母、分子を \(\cos \alpha \cos \beta\) で割ると、
\(\begin{align}\displaystyle \tan (\alpha + \beta) &= \displaystyle \frac{\frac{\sin \alpha}{\cos \alpha} + \frac{\sin \beta}{\cos \beta}}{1 − \frac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\ &= \displaystyle \frac{\tan \alpha + \tan \beta}{1 − \tan \alpha \tan \beta}\end{align}\)
よって
\(\color{red}{\displaystyle \tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 − \tan \alpha \tan \beta}}\)
また、\(\beta\) を \(−\beta\) に置き換えると、
\(\displaystyle \tan (\alpha − \beta) = \frac{\tan \alpha + \tan (−\beta)}{1 − \tan \alpha \tan (−\beta)}\)
\(\tan (−\beta) = −\tan \beta\) であるから、
\(\color{red}{\displaystyle \tan (\alpha − \beta) = \frac{\tan \alpha − \tan \beta}{1 + \tan \alpha \tan \beta}}\)
以上より、tan の加法定理が成り立つ。
(証明終わり)
計算が多くて大変でしたが、無事証明できましたね。
証明全体を丸暗記するというよりも、それぞれの加法定理を導くおおまかな流れを理解しておきましょう!
加法定理の計算問題
計算問題を通して、加法定理の使い方を説明します。
計算問題①「sin 15°」
\(\sin 15^\circ\) を求めよ。

問題の角度を、三角比がわかっている角度(\(30^\circ\), \(45^\circ\), \(60^\circ\), \(90^\circ\) など)の和や差で表すと、加法定理を使えます。
今回の場合、\(15^\circ = 45^\circ − 30^\circ\)と表すことができますね。
\(15^\circ = 45^\circ − 30^\circ\)

加法定理より、
\(\begin{align} \sin 15^\circ &= \sin (45^\circ − 30^\circ) \\ &= \sin 45^\circ \cos 30^\circ − \cos 45^\circ \sin 30^\circ \\ &= \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} − \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ &= \frac{\sqrt{6}}{4} − \frac{\sqrt{2}}{4} \\ &= \frac{\sqrt{6} − \sqrt{2}}{4} \end{align}\)
答え: \(\color{red}{\displaystyle \frac{\sqrt{6} − \sqrt{2}}{4}}\)
代表的な角度(\(30^\circ\), \(45^\circ\), \(60^\circ\), \(90^\circ\) など)の三角比は、一通りわかるようにしておきましょう。
解答のように、単位円にささっと書いて確認するのがオススメです。
ちょっとあやしいなと思った人は以下の記事で復習してくださいね!
 三角関数表(1°ごとの三角比の表)と有名角の三角比の求め方!
三角関数表(1°ごとの三角比の表)と有名角の三角比の求め方!
計算問題②「tan 75°」
\(\tan 75^\circ\) を求めよ。

\(75^\circ\) はどのように表せるでしょうか?
また、\(\tan\) の加法定理は符号の関係に注意しましょう!
\(75^\circ = 45^\circ + 30^\circ\)

加法定理より、
\(\begin{align} \tan 75^\circ &= \tan (45^\circ + 30^\circ) \\ &= \frac{\tan 45^\circ + \tan 30^\circ}{1 − \tan 45^\circ \tan 30^\circ} \\ &= \frac{1 + \frac{1}{\sqrt{3}}}{1 − \frac{1}{\sqrt{3}}} \\ &= \frac{\sqrt{3} + 1}{\sqrt{3} − 1} \\ &= \frac{4 + 2\sqrt{3}}{2} \\ &= 2 + \sqrt{3} \end{align}\)
答え: \(\color{red}{2 + \sqrt{3}}\)
角度の和・差への置き換えには慣れてきましたか?
計算問題③「cos 11/12 π」
弧度法(ラジアン)の角についても、練習しておきましょう。
\(\displaystyle \cos \frac{11}{12} \pi\) を求めよ。

ラジアン表記でも、考え方は同じです。角をどう分解できるか考えてみましょう。
\(\begin{align} \frac{11}{12} \pi &= \frac{9}{12} \pi + \frac{2}{12} \pi \\ &= \frac{3}{4} \pi + \frac{\pi}{6} \end{align}\)

加法定理より、
\(\begin{align} \cos \frac{11}{12} \pi &= \cos \left(\frac{3}{4} \pi + \frac{\pi}{6}\right) \\ &= \cos \frac{3}{4} \pi \cos \frac{\pi}{6} − \sin \frac{3}{4} \pi \sin \frac{\pi}{6} \\ &= −\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} − \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ &= −\frac{\sqrt{6}}{4} − \frac{\sqrt{2}}{4} \\ &= −\frac{\sqrt{6} + \sqrt{2}}{4} \end{align}\)
答え: \(\color{red}{\displaystyle −\frac{\sqrt{6} + \sqrt{2}}{4}}\)
計算問題④「sin 5/12 π」
\(\displaystyle \sin \frac{5}{12} \pi\) を求めよ。

分母分子が約分できる分数同士に分けるのがポイントです。
\(\begin{align} \frac{5}{12} \pi &= \frac{2}{12} \pi + \frac{3}{12} \pi \\ &= \frac{\pi}{6} + \frac{\pi}{4} \end{align}\)

加法定理より、
\(\begin{align} \sin \frac{5}{12} \pi &= \sin \left(\frac{\pi}{6} + \frac{\pi}{4}\right) \\ &= \sin \frac{\pi}{6} \cos \frac{\pi}{4} + \cos \frac{\pi}{6} \sin \frac{\pi}{4} \\ &= \frac{1}{2} \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} \\ &= \frac{\sqrt{2} + \sqrt{6}}{4} \end{align}\)
答え: \(\color{red}{\displaystyle \frac{\sqrt{2} + \sqrt{6}}{4}}\)
加法定理の応用問題
最後に、加法定理の応用問題に挑戦しましょう。
問題の角度をうまくほかの角度の和と差に変換し、加法定理の便利さを実感してくださいね。
応用問題①「三倍角の公式の証明」
\(\sin 3\theta = 3\sin \theta − 4\sin^3 \theta\) となることを証明せよ。

この式、実は三倍角の公式です。
加法定理で \(3\theta\) を小さく分解し、三角比の相互関係 \(\displaystyle \sin^2 \theta + \cos^2 \theta = 1\) で三角比を \(\sin\) に統一していくと証明できます。
\(3\theta = \theta + 2\theta\) として加法定理を使うと、
\(\begin{align} \ \ (\text{左辺}) &= \sin (\theta + 2\theta)\\&= \sin \theta \cos 2\theta + \cos \theta \sin 2\theta\end{align}\)
さらに、\(2\theta = \theta + \theta\) として加法定理を使うと、
\((\text{左辺})\)
\(= \sin \theta \cos (\theta + \theta) + \cos \theta \sin (\theta + \theta)\)
\(= \sin \theta(\cos \theta \cos \theta − \sin \theta \sin \theta) \) \(+ \cos \theta(\sin \theta \cos \theta + \cos \theta \sin \theta)\)
\(= \sin \theta \cos^2\theta − \sin^3\theta \) \(+ \sin \theta \cos^2\theta + \sin \theta \cos^2\theta\)
\(= 3\sin \theta \cos^2\theta − \sin^3\theta\)
\(= 3\sin \theta(1 − \sin^2\theta) − \sin^3\theta\)(三角比の相互関係)
\(= 3\sin \theta − 4\sin^3\theta\)
\(= (\text{右辺})\)
(証明終わり)
応用問題②「cos (α + β) を求めよ」
\(\alpha\), \(\beta\) が第四象限の角で \(\displaystyle \sin \alpha = −\frac{1}{5}\), \(\displaystyle \cos \beta = \frac{1}{3}\) であるとき、\(\cos (\alpha + \beta)\) を求めよ。

加法定理を使うと、\(\cos (\alpha + \beta)\) は \(\sin \alpha\), \(\sin \beta\), \(\cos \alpha\), \(\cos \beta\) で表せますね。
三角比の相互関係を利用して先に \(\cos \alpha\), \(\sin \beta\) を求めておきましょう。
また、象限の情報から \(\cos \alpha\), \(\sin \beta\) の符号は必ず確認しておいてくださいね!
三角比の相互関係 \(\sin^2 \theta + \cos^2 \theta = 1\) より、
\(\cos^2 \alpha = 1 − \sin^2 \alpha\)
\(\begin{align} \cos \alpha &= \pm \sqrt{1 − \sin^2 \alpha} \\ &= \pm \sqrt{1 − \left( −\frac{1}{5} \right)^2} \\ &= \pm \sqrt{1 − \frac{1}{25}} \\ &= \pm \sqrt{\frac{24}{25}} \\ &= \pm \frac{2\sqrt{6}}{5} \end{align}\)
\(\alpha\) が第四象限にあることから、\(\cos \alpha > 0\)
よって
\(\displaystyle \cos \alpha = \frac{2\sqrt{6}}{5}\)
同様に、
\(\sin^2 \beta = 1 − \cos^2 \beta\)
\(\begin{align}\sin \beta &= \pm \sqrt{1 − \cos^2 \beta} \\ &= \pm \sqrt{1 − \left( \frac{1}{3} \right)^2} \\ &= \pm \sqrt{1 − \frac{1}{9}} \\ &= \pm \sqrt{\frac{8}{9}} \\ &= \pm \frac{2\sqrt{2}}{3} \end{align}\)
\(\beta\) が第四象限にあることから、\(\sin \beta < 0\)
よって
\(\displaystyle \sin \beta = −\frac{2\sqrt{2}}{3}\)
加法定理より、
\(\cos (\alpha + \beta)\)
\(= \cos \alpha \cos \beta − \sin \alpha \sin \beta\)
\(= \displaystyle \frac{2\sqrt{6}}{5} \cdot \frac{1}{3} − \left( −\frac{1}{5} \right) \cdot \left( −\frac{2\sqrt{2}}{3} \right)\)
\(= \displaystyle \frac{2(\sqrt{6} − \sqrt{2})}{15}\)
答え: \(\color{red}{\displaystyle \frac{2(\sqrt{6} − \sqrt{2})}{15}}\)
【補足】加法定理から導ける公式
加法定理から導出できる公式は次のとおりです。
| 二倍角の公式 |
\begin{align}\sin2\theta = 2\sin\theta\cos\theta \end{align} \begin{align}\cos2\theta &= \cos^2\theta − \sin^2\theta \\ &= 1 − 2\sin^2\theta \\ &= 2\cos^2\theta − 1 \end{align} \begin{align}\displaystyle \tan2\theta = \frac{2\tan\theta}{1 − \tan^2\theta}\end{align} |
|---|---|
| 三倍角の公式 |
\begin{align}\sin3\theta = 3\sin\theta − 4\sin^3\theta\end{align} \begin{align}\cos3\theta = −3\cos\theta + 4\cos^3\theta\end{align} |
| 半角の公式 |
\begin{align}\displaystyle \sin^2 \frac{\theta}{2} = \frac{1 − \cos\theta}{2}\end{align} \begin{align}\displaystyle \cos^2 \frac{\theta}{2} = \frac{1 + \cos\theta}{2}\end{align} \begin{align}\displaystyle \tan^2 \frac{\theta}{2} = \frac{1 − \cos\theta}{1 + \cos\theta}\end{align} |
| 和積の公式 |
\begin{align}\displaystyle \sin A + \sin B = 2\sin\frac{A + B}{2}\cos\frac{A − B}{2}\end{align} \begin{align}\displaystyle \sin A − \sin B = 2\cos\frac{A + B}{2}\sin\frac{A − B}{2}\end{align} \begin{align}\displaystyle \cos A + \cos B = 2\cos\frac{A + B}{2}\cos\frac{A − B}{2}\end{align} \begin{align}\displaystyle \cos A − \cos B = −2\sin\frac{A + B}{2}\sin\frac{A − B}{2}\end{align} |
| 積和の公式 |
\begin{align}\displaystyle \sin\alpha\cos\beta = \frac{1}{2} \{\sin(\alpha + \beta) + \sin(\alpha − \beta)\}\end{align} \begin{align}\displaystyle \cos\alpha\sin\beta = \frac{1}{2} \{\sin(\alpha + \beta) − \sin(\alpha − \beta)\}\end{align} \begin{align}\displaystyle \cos\alpha\cos\beta = \frac{1}{2} \{\cos(\alpha + \beta) + \cos(\alpha − \beta)\}\end{align} \begin{align}\displaystyle \sin\alpha\sin\beta = −\frac{1}{2} \{\cos(\alpha + \beta) − \cos(\alpha − \beta)\}\end{align} |
加法定理からの具体的な導出方法については、以下の個別記事で解説しています。
以上で加法定理の解説は終わりです。
加法定理を覚えていれば、三角関数のほとんどの公式は簡単に導出できます。
とっても重要な定理なので、必ずマスターしておきましょう!
三角関数に関するほかの定理や公式について調べたい方は、以下のまとめ記事から探してみてください!
 三角比・三角関数を総まとめ!定義・定理・公式一覧
三角比・三角関数を総まとめ!定義・定理・公式一覧









