この記事では、「確率分布」と「確率変数」の意味や種類、基本的な公式をわかりやすく解説します。
確率分布の期待値(平均)、分散などの求め方も計算問題を通して説明しますので、ぜひこの記事を通してマスターしてくださいね!
確率分布・確率変数とは?
「コインを \(5\) 回投げて表が \(4\) 回以上出る」「身長が高校の中でトップ \(10\) %以内に入る」
どちらも、確率論で考えられそうですよね。
確率分布と確率変数は、上記の例のように偶然性(ランダムネス)に支配され、確率的に決まる現象を記述し、可視化するために使われる考え方です。
- 確率変数
ある試行の結果によってその値がランダムに定まり、各値に対応して確率が定まるような変数 - 確率分布(分布)
確率変数 \(X\) のとりうる値と、その値をとる確率 \(P\) との対応関係
確率変数 \(X\) のとりうる値が \(x_1, x_2, \cdots, x_n\) で、それぞれの値をとる確率が \(p_1, p_2, \cdots, p_n\) であるとき、\(X\) の確率分布(\(X\) と \(P\) の対応関係)は次のように表される。
|
\(X\) |
\(x_1\) |
\(x_2\) |
\(\cdots\) |
\(x_n\) |
計 |
|
\(P\) |
\(p_1\) |
\(p_2\) |
\(\cdots\) |
\(p_n\) |
\(1\) |
このとき、「確率変数 \(X\) はこの分布に従う」という。
上記のように、確率分布を表にしたものを「確率分布表」といいます。
確率分布の種類
確率分布は、「離散型確率分布」と「連続型確率分布」の \(2\) 種類に大別できます。
冒頭に挙げた例の確率分布を、確率変数 \(X\) の値を横軸にとったグラフとして表して見ましょう。
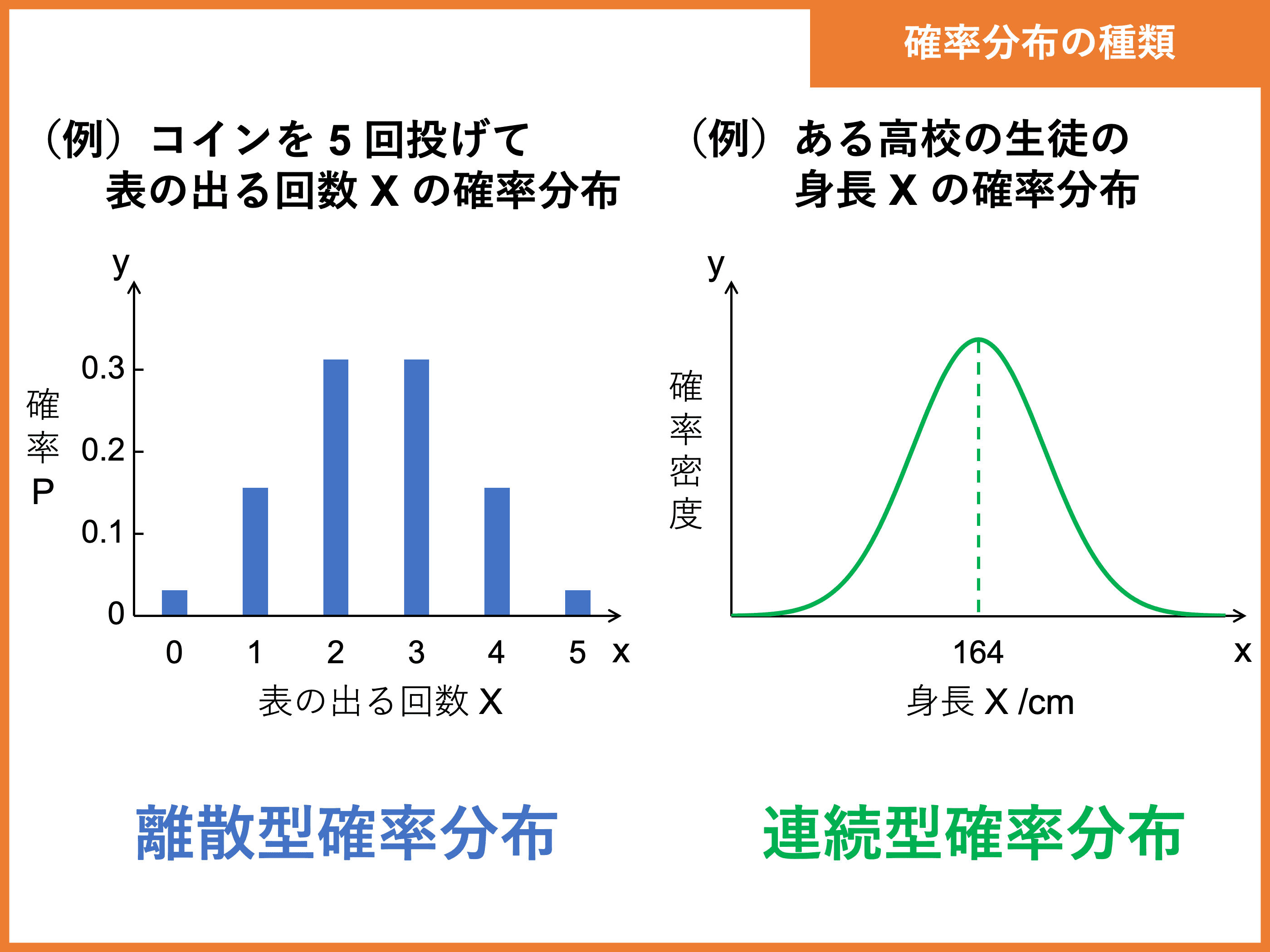
コインの例のように棒グラフで表せるものを「離散型確率分布」、身長の例のように曲線的に表せるものを「連続型確率分布」といいます。
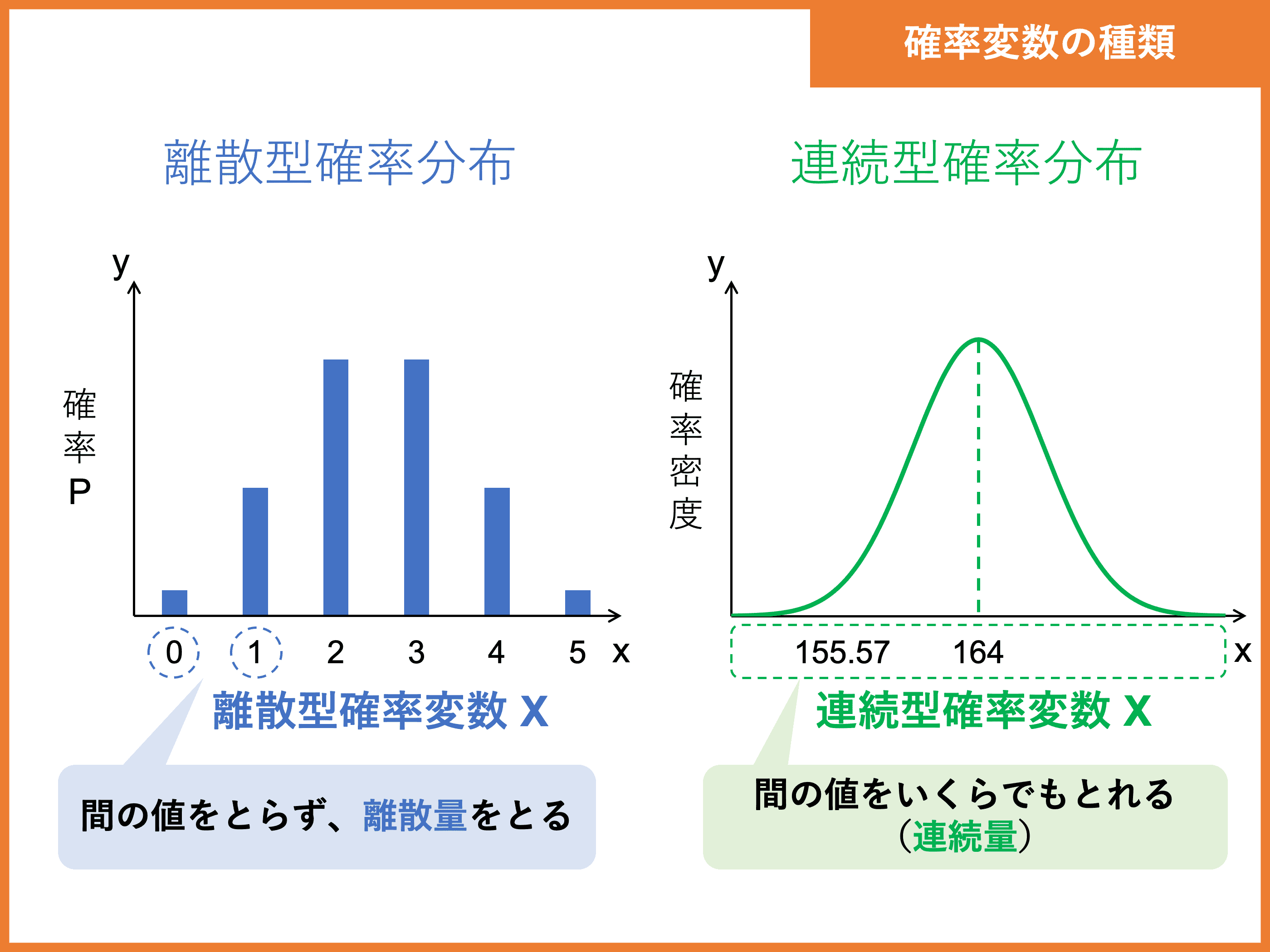
離散型確率変数と連続型確率変数
両者の違いは、確率変数の値の連続性によって決まります。
「コインの表が出る回数」のように、離散量(とびとびの値)をとる確率変数を「離散型確率変数」といいます。
一方で、「高校生の身長」のように、連続量をとる確率変数を「連続型確率変数」といいます。
離散型では縦軸の値の足し算 \(\displaystyle \sum_{k = a}^b p_k\) が、連続型では曲線下の面積 \(\displaystyle \int_a^b f(x) \ dx\) が確率を表します。
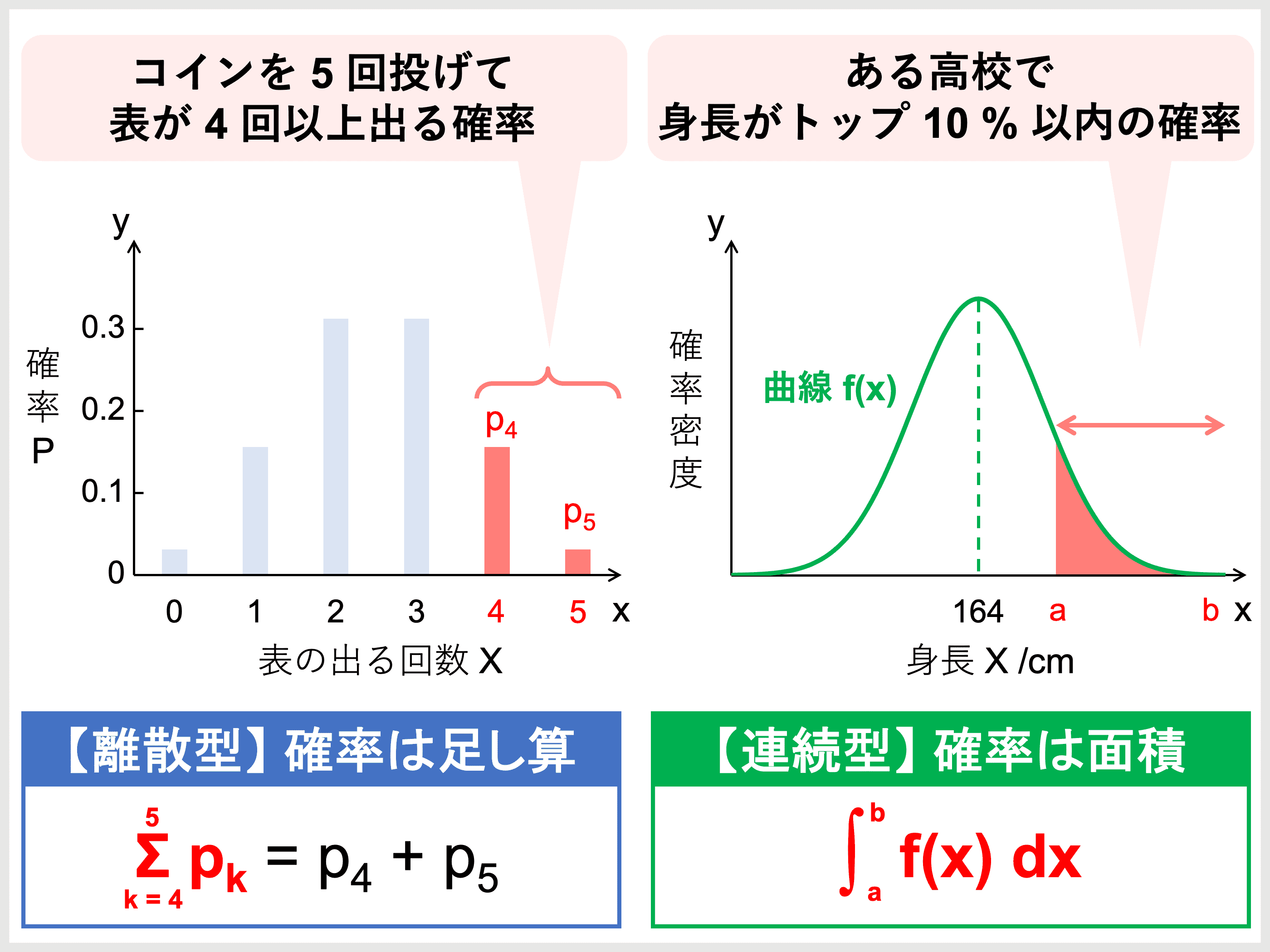
連続型における曲線 \(f(x)\) を「確率密度関数」といいます。
 確率密度関数とは?連続型確率変数の期待値・分散の求め方
確率密度関数とは?連続型確率変数の期待値・分散の求め方
「離散型」⇄「連続型」は変換できる
このように、データ(確率変数)は値の連続性に応じて「離散型」と「連続型」に分類できます。
しかしながら、状況に応じて「離散型データを連続型データとして」「連続型データを離散型データとして」扱うこともできます。
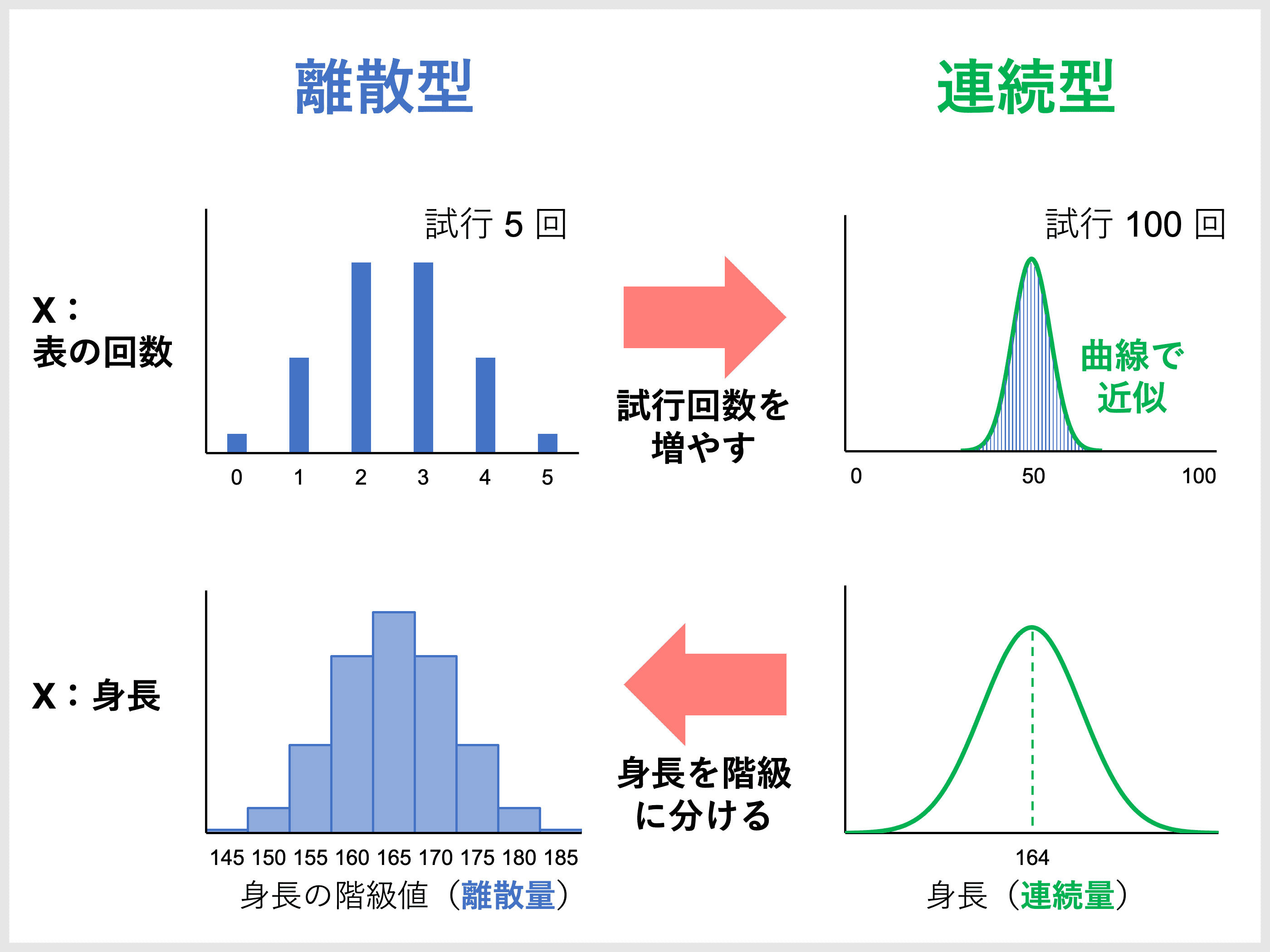
- 離散型→データ数を増やせば連続型とみなす(= 近似する)ことができる
- 連続型→値を階級ごとに区切れば離散型とみなすことができる
なお、以降に示す公式は離散型を前提にしています。
離散型と連続型は具体的な求め方(和か積分か)が違うだけで、根底の考え方はまったく同じです。
そのため、離散型のあとに連続型を勉強すると理解しやすくなりますよ。
確率分布のルール
ここでは、確率分布の表記ルールや、基本的な性質について説明します。
確率の表記
確率変数がある値(またはある範囲の値)をとるとき、そのときの確率は次のように表します。
- 確率変数 \(X\) が値 \(a\) をとる確率
\begin{align}P(X = a)\end{align} - \(X\) が \(a\) 以上 \(b\) 以下の値をとる確率
\begin{align}P(a \leq X \leq b)\end{align}
確率分布の性質
確率分布における確率には、次の \(2\) つの性質があります。
\(P(X = x_k) = p_k\) \((k = 1, 2, 3, \cdots, n)\) であるとき、次が成り立つ。
- 確率は負の値をとらない
\begin{align}p_k \geq 0\end{align} - 確率の和は必ず \(1\) になる
\begin{align}\displaystyle \sum_{k = 1}^n p_k = p_1 + p_2 + \cdots + p_n = 1\end{align}
確率分布の期待値・分散・標準偏差の公式
ここでは、確率分布の特徴を示す統計量、「確率変数の期待値(平均)」「確率変数の分散」「確率変数の標準偏差」の公式を示します。
確率変数の期待値(平均) \(E(X)\), \(m\)
確率変数 \(X\) のとりうる各値と確率をかけて、それらをすべて足した値を \(X\) の「期待値」または「平均」といい、\(E(X)\) または \(m\) で表します。
確率変数 \(X\) において、\(P(X = x_k) = p_k\) \((k = 1, 2, 3, \cdots, n)\) であるとき、
\(X\) の期待値は
\begin{align}E(X) = m &= \sum_{k = 1}^n x_kp_k \\&= x_1p_1 + x_2p_2 + \cdots + x_np_n\end{align}
このとき、確率変数 \(X\) の各値と期待値(平均 \(m\))との差を偏差 \((X − m)\) といいます。
確率変数の分散 \(V(X)\)
確率変数 \(X\) の偏差の二乗 \((X − m)^2\) の期待値(平均)を \(X\) の「分散」といい、\(V(X)\) で表します。
確率変数 \(X\) において、\(P(X = x_k) = p_k\) \((k = 1, 2, 3, \cdots, n)\) であるとき、\(X\) の期待値を \(m\) とすると、\(X\) の分散 \(V(X)\) は
\begin{align}V(X) &= E((X − m)^2) \\&= \sum_{k = 1}^n (x_k − m)^2p_k \\&= (x_1 − m)^2p_1 + (x_2 − m)^2p_2 + \cdots + (x_n − m)^2p_n\end{align}
(見切れる場合は横へスクロール)
なお、\(V(X)\) は \((X^2 \ \text{の期待値}) − (X \ \text{の期待値})^2\) でも求められる。
\begin{align}V(X) = E(X^2) − \{E(X)\}^2\end{align}
\(2\) つ目の公式の方が計算が楽になることも多いので、どちらの公式もしっかり覚えておきましょう!
\(2\) つ目の公式は、\(1\) つ目の公式を式変形すると導けます。
\(\begin{align}V(X) &= \color{red}{E((X − m)^2)} \\&= \sum_{k = 1}^n (x_k − m)^2p_k \\&= \sum_{k = 1}^n (x_k^2 − 2mx_k + m^2)p_k \\&= \sum_{k = 1}^n x_k^2p_k − 2m \sum_{k = 1}^n x_kp_k + m^2 \sum_{k = 1}^n p_k \end{align}\)
ここで、\(\displaystyle \sum_{k = 1}^n x_k^2p_k = E(X^2)\), \(\displaystyle \sum_{k = 1}^n x_kp_k = E(X) = m\), \(\displaystyle \sum_{k = 1}^n p_k = 1\) であるから、
\(\begin{align}V(X) &= \sum_{k = 1}^n x_k^2p_k − 2m \sum_{k = 1}^n x_kp_k + m^2 \sum_{k = 1}^n p_k \\&= E(X^2) − 2m^2 + m^2 \\&= E(X^2) − m^2 \\&= \color{red}{E(X^2) − \{E(X)\}^2} \end{align}\)
(証明終わり)
途中の式変形はシグマ \(\sum\) の計算規則に従っています。
 シグマ Σ とは?記号の意味や和の公式、証明や計算問題
シグマ Σ とは?記号の意味や和の公式、証明や計算問題
確率変数の標準偏差 \(\sigma(X)\)
確率変数 \(X\) の分散 \(V(X)\) の正の平方根を「標準偏差」といい、\(\sigma(X)\) (または \(s(X)\) など)で表します。
確率変数 \(X\) の分散を \(V(X)\) とすると、\(X\) の標準偏差 \(\sigma(X)\) は
\begin{align}\sigma(X) = \sqrt{V(X)}\end{align}
分散 \(V(X)\) の単位は \(X\) の \(2\) 乗になっているため、平方根をとって \(X\) と単位を合わせた標準偏差 \(\sigma(X)\) はばらつきの指標として使い勝手がよいといえます。
平均(期待値)、分散、標準偏差の考え方や求め方は、数Aの「データの分析」と全く同じです。
記号や言い回しが違うだけなので、関連性を頭の中で整理しておくといいですね!
 データの分析を総まとめ!数Iで習う公式一覧と裏ワザ
データの分析を総まとめ!数Iで習う公式一覧と裏ワザ
確率変数 \(aX + b\) の計算規則
確率変数 \(X\) に対して、一次式 \(aX + b\) も確率変数であり、以下の計算規則が成り立ちます。
\(X\) を確率変数、\(a\), \(b\) を \(0\) でない定数とする。
- \(aX + b\) の期待値(平均)
\begin{align}E(aX + b) = aE(x) + b\end{align} - \(aX + b\) の分散
\begin{align}V(aX + b) = a^2V(x)\end{align} - \(aX + b\) の標準偏差
\begin{align}\sigma(aX + b) = |a|\sigma(x)\end{align}
\(E(aX + b)\) は、元の期待値 \(E(X)\) を \(a\) 倍し、\(b\) を足した値になります。
一方、ばらつきを表す分散 \(V(aX + b)\) と標準偏差 \(\sigma(aX + b)\) には、一律に足した \(b\) の大きさは影響せず、\(a\) の影響だけがかかります。
確率変数 \(X\) と確率変数 \(aX + b\) は \(1\) 対 \(1\) で対応するので、同じ確率分布をもちます。

よって、\(E(aX + b)\), \(V(aX + b)\), \(\sigma(aX + b)\) はそれぞれ次のように計算できます。
\(\begin{align}E(aX + b) &= \displaystyle \sum_{k = 1}^n (ax_k + b)p_k \\&= \displaystyle a \sum_{k = 1}^n x_kp_k + b\sum_{k = 1}^n p_k\end{align}\)
ここで、\(E(X) = \displaystyle \sum_{k = 1}^n x_kp_k\), \(\displaystyle \sum_{k = 1}^n p_k = 1\) であるから
\(\begin{align}E(aX + b) &= \displaystyle a \sum_{k = 1}^n x_kp_k + b\sum_{k = 1}^n p_k\\&= \color{red}{aE(X) + b}\end{align}\)
\(V(aX + b)\)
\(= E((aX + b)^2) − \{E(aX + b)\}^2\)
\(= E(a^2X^2 + 2abX + b^2) − \{aE(X) + b\}^2\)
\(= a^2E(X^2) + 2abE(X) + b^2 − [a^2\{E(X)\}^2 + 2abE(X) + b^2]\)
\(= a^2E(X^2) + 2abE(X) + b^2 − a^2\{E(X)\}^2 − 2abE(X) − b^2\)
\(= a^2[E(X^2) − \{E(X)\}^2]\)
\(= \color{red}{a^2V(X)}\)
(見切れる場合は横へスクロール)
\(\begin{align}\sigma(aX + b) &= \sqrt{V(aX + b)}\\&= \sqrt{a^2V(X)}\\&= |a|\sqrt{V(X)}\\&= \color{red}{|a|\sigma(X)}\end{align}\)
(証明終わり)
複数の確率変数の扱い方
ここでは、\(2\) つ以上の確率変数を同時に扱う際の考え方を説明します。
同時分布
ある試行によって、\(2\) つ以上の変数の値が同時に定まるとき、それらの値と確率の対応を「同時分布」といいます。
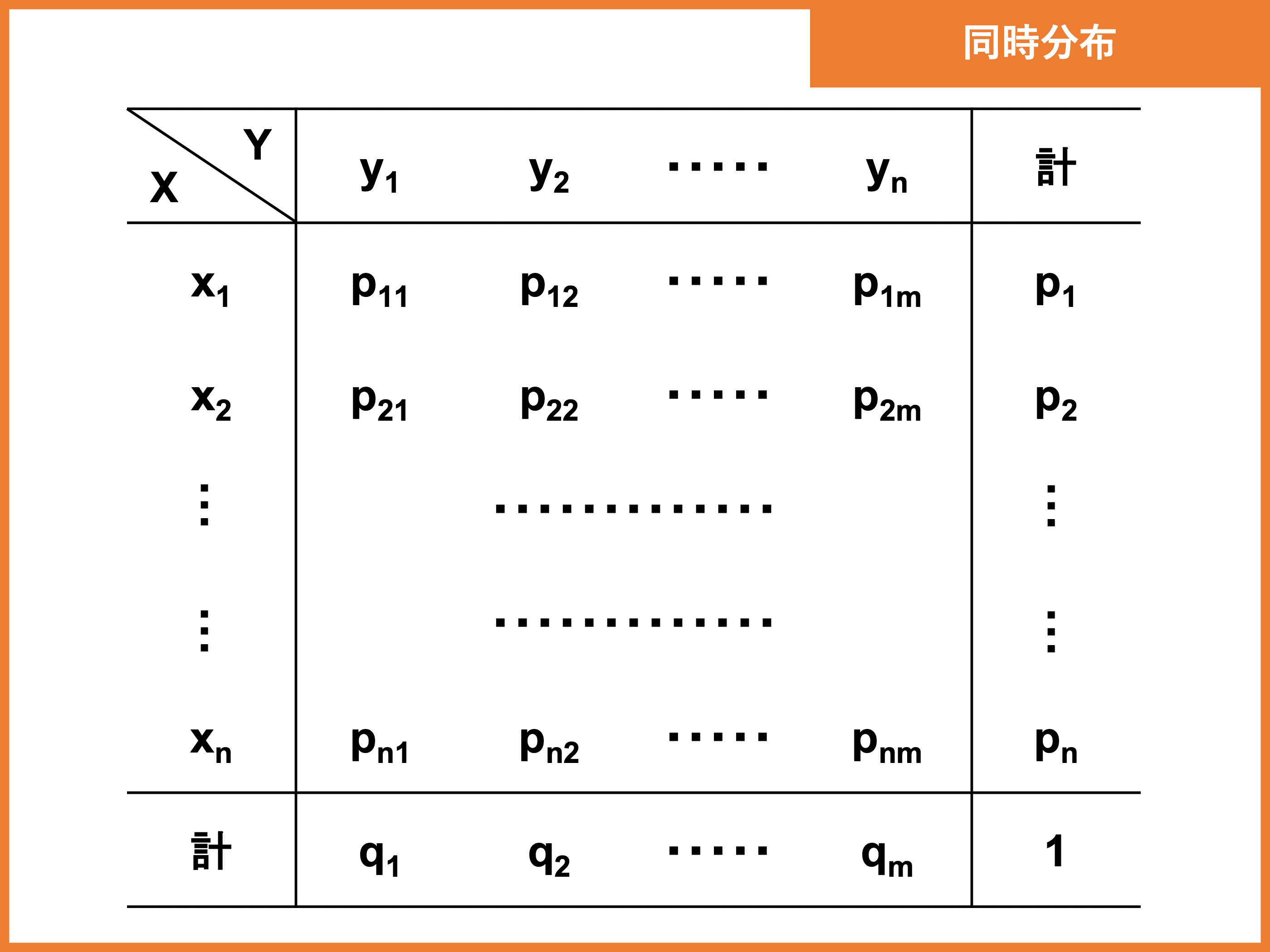
同時分布における確率は次のように表します。
確率変数 \(X, Y\) について、\(X = a\) かつ \(Y = b\) である確率は
\begin{align}P(X = a, Y = b)\end{align}
なお、確率変数が \(3\) つ以上に増えても同じ要領で記述できます。
確率変数 \(x_i\) \(i = 1, 2, \cdots, n\) について、
\(X_1 = a_1\) かつ \(X_2 = a_2\) かつ \(\cdots\) かつ \(X_n = a_n\) である確率
\begin{align}P(X_1 = a_1, X_2 = a_2, \cdots, X_n = a_n)\end{align}
確率変数の独立性を考えよう
\(2\) つ以上の確率変数を扱うときは、確率変数同士が独立であるか従属であるかに注意する必要があります。
変数 \(X, Y\) について、
\begin{align}P(X = a, Y = b) = P(X = a) \cdot P(Y = b)\end{align}
が \(a, b\) の値によらず常に成り立つとき、「確率変数 \(X, Y\) は互いに独立である」という。
こちらも、確率変数が \(3\) つ以上に増えても同じ要領で記述できます。
変数 \(X_i \ (i = 1, 2, \cdots, n)\) について、
\begin{align}&P(X_1 = a_1, X_2 = a_2, \cdots, X_n = a_n) \\&= P(X_1 = a_1) \cdot P(X_2 = a_2) \cdot \cdots \cdot P(X_n = a_n)\end{align}
(見切れる場合は横へスクロール)
が \(a_i\) の値によらず常に成り立つとき、確率変数 \(X_1, X_2, \cdots, X_n\) は互いに独立である。
確率変数同士が独立か従属かを知るには、それぞれの事象が独立か従属かを確認します。
事象 \(A, B\) が互いに独立ならば、
\begin{align}P_A(B) = P(B) &\iff P_B(A) = P(A) \\&\iff P(A \cap B) = P(A)P(B)\end{align}
(見切れる場合は横へスクロール)
が成り立つ。
一方、事象 \(A, B\) が互いに独立でないとき、「\(A\) と \(B\) は従属である」という。
条件付き確率
ある事象が起きたという条件のもとで別の事象が起きる確率。
(例)\(P_A(B)\) :「事象 \(A\) が起きたという条件のもとで事象 \(B\) が起きる確率」
 条件付き確率とは?公式や問題、ベイズの定理(不良品の例)も!
条件付き確率とは?公式や問題、ベイズの定理(不良品の例)も!
複数の確率変数の期待値の性質
確率変数の和や積の期待値には、次の性質が成り立ちます。
確率変数 \(X\), \(Y\) について、
\begin{align}E(X + Y) = E(X) + E(Y)\end{align}
一般に、\(3\) つ以上の確率変数 \(X_1\), \(X_2\), \(\cdots\), \(X_n\) についても、
\begin{align}E(X_1 + X_2 + \cdots + X_n) = E(X_1) + E(X_2) + \cdots + E(X_n)\end{align}
(見切れる場合は横へスクロール)
確率変数 \(X\), \(Y\) について、
\begin{align}E(aX + bY) = aE(X) + bE(Y)\end{align}
(ただし \(a\), \(b\) は \(0\) でない定数)
一般に、\(3\) つ以上の確率変数 \(X_1\), \(X_2\), \(\cdots\), \(X_n\) についても、
\begin{align}E(a_1X_1 + a_2X_2 + \cdots + a_nX_n) = a_1E(X_1) + a_2E(X_2) + \cdots + a_nE(X_n)\end{align}
(見切れる場合は横へスクロール)
(ただし \(a_i\) \((i = 1, 2, \cdots, n)\) は \(0\) でない定数)
確率変数 \(X\), \(Y\) が互いに独立ならば
\begin{align}E(XY) = E(X)E(Y)\end{align}
一般に、互いに独立な \(3\) つ以上の確率変数 \(X_1\), \(X_2\), \(\cdots\), \(X_n\) についても、
\begin{align}E(X_1X_2 \cdots X_n) = E(X_1) \cdot E(X_2) \cdot \cdots \cdot E(X_n)\end{align}
(見切れる場合は横へスクロール)
積の期待値だけ、「確率変数同士が独立」という条件があることを覚えておきましょう。
複数の確率変数の分散の性質
確率変数の和の分散には、次の性質が成り立ちます。
確率変数 \(X\), \(Y\) が互いに独立ならば
\begin{align}V(X + Y) = V(X) + V(Y)\end{align}
一般に、互いに独立な \(3\) つ以上の確率変数 \(X_1\), \(X_2\), \(\cdots\), \(X_n\) についても、
\begin{align}V(X_1 + X_2 + \cdots + X_n) = V(X_1) + V(X_2) + \cdots + V(X_n)\end{align}
(見切れる場合は横へスクロール)
確率変数 \(X\), \(Y\) が互いに独立ならば
\begin{align}V(aX + bY) = a^2V(X) + b^2V(Y)\end{align}
(ただし \(a\), \(b\) は \(0\) でない定数)
一般に、互いに独立な \(3\) つ以上の確率変数 \(X_1\), \(X_2\), \(\cdots\), \(X_n\) についても、
\begin{align}V(a_1X_1 + a_2X_2 + \cdots + a_nX_n) = a_1^2V(X_1) + a_2^2V(X_2) + \cdots + a_n^2V(X_n)\end{align}
(見切れる場合は横へスクロール)
(ただし \(a_i\) \((i = 1, 2, \cdots, n)\) は \(0\) でない定数)
分散の公式を使うには、常に「確率変数同士が独立」という条件が前提となることを覚えておきましょう。
確率分布の計算問題
それでは、確率分布の基本的な計算問題に挑戦してみましょう。
計算問題①「\(E(X)\), \(V(X)\), \(\sigma(X)\) を求める」
\(1\) から \(6\) までの数字の中から、重複しないように \(3\) つの数字を無作為に選んだとき、その中の最大の数字を \(X\) とする。確率変数 \(X\) の期待値 \(E(X)\)、分散 \(V(X)\) および標準偏差 \(\sigma(X)\) を求めよ。

問題文をよく読んで、まずは \(X\) がとりうる値を考えましょう。
確率分布を得るには、場合の数と確率の考え方を利用します。
\(X\) のとりうる値は \(X = 3, 4, 5, 6\)
\(X = i\) である場合の数は、\(3\) つの数字のうち \(1\) つが \(i\) で、\(i − 1\) 以下の他の \(2\) つを選べばよいから
\({}_{i − 1} \mathrm{C}_2 = \displaystyle \frac{(i − 1)(i − 2)}{2}\) (通り)
また、\(6\) つの数字から \(3\) つ選ぶ場合の数は
\({}_6 \mathrm{C}_3 = \displaystyle \frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} = 20\)(通り)
よって
\(\begin{align}P(X = i) &= \displaystyle \frac{{}_{i − 1} \mathrm{C}_2}{{}_6 \mathrm{C}_3} \\&= \displaystyle \frac{(i − 1)(i − 2)}{40} \ (i = 3, 4, 5, 6)\end{align}\)
\(X\) の確率分布は次のようになる。
|
\(X\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
計 |
|
\(P\) |
\(\displaystyle \frac{1}{20}\) |
\(\displaystyle \frac{3}{20}\) |
\(\displaystyle \frac{6}{20}\) |
\(\displaystyle \frac{10}{20}\) |
\(1\) |
したがって、
\(X\) の期待値 \(E(X)\) は
\(E(X)\)
\(= 3 \cdot \displaystyle \frac{1}{20} + 4 \cdot \displaystyle \frac{3}{20} + 5 \cdot \displaystyle \frac{6}{20} + 6 \cdot \displaystyle \frac{10}{20}\)
\(= \displaystyle \frac{3 + 12 + 30 + 60}{20}\)
\(= \displaystyle \frac{105}{20}\)
\(= \displaystyle \frac{21}{4}\)
また
\(E(X^2)\)
\(= 3^2 \cdot \displaystyle \frac{1}{20} + 4^2 \cdot \displaystyle \frac{3}{20} + 5^2 \cdot \displaystyle \frac{6}{20} + 6^2 \cdot \displaystyle \frac{10}{20}\)
\(= \displaystyle \frac{9 + 48 + 150 + 360}{20}\)
\(= \displaystyle \frac{567}{20}\)
より、
分散 \(V(X)\) および標準偏差 \(\sigma(X)\) は
\(\begin{align}V(X) &= E(X^2) − \{E(X)\}^2 \\&= \displaystyle \frac{567}{20} − \left(\displaystyle \frac{21}{4}\right)^2 = \displaystyle \frac{567}{20} − \displaystyle \frac{441}{16} \\&= \displaystyle \frac{2268 − 2205}{80} \\&= \displaystyle \frac{63}{80}\end{align}\)
\(\sigma(X) = \sqrt{V(X)} = \sqrt{\displaystyle \frac{63}{80}} = \displaystyle \frac{3\sqrt{35}}{20}\)
答え: \(E(X) = \displaystyle \frac{21}{4}\)、\(V(X) = \displaystyle \frac{63}{80}\)、\(\sigma(X) = \displaystyle \frac{3\sqrt{35}}{20}\)
計算問題②「\(E(2X + 5)\), \(V(2X + 5)\) を求める」
\(1\) から \(17\) までの整数を \(1\) つずつ記入した \(17\) 枚のカードがある。この中から無作為に \(1\) 枚のカードを抜き取り、記入してある数を \(X\) とする。\(X\) は確率変数である。
確率変数 \(2X + 5\) の平均 \(E(2X + 5)\)、分散 \(V(2X + 5)\) を求めよ。

\(E(X)\), \(V(X)\) を求め、一次式の確率変数の公式に当てはめます。
自然数の和および自然数の平方の和を求めるときは、\(\sum\) の公式を思い出しましょう。
Σの公式
・\(\displaystyle \sum_{k = 1}^n k = \displaystyle \frac{1}{2}n(n + 1)\)
・\(\displaystyle \sum_{k = 1}^n k^2 = \displaystyle \frac{1}{6}n(n + 1)(2n + 1)\)
 シグマ Σ とは?記号の意味や和の公式、証明や計算問題
シグマ Σ とは?記号の意味や和の公式、証明や計算問題
\(\begin{align}E(X) &= \displaystyle \frac{1}{17}(1 + 2 + \cdots + 17) \\&= \displaystyle \frac{1}{17} \cdot \frac{17(17 + 1)}{2} \\&= 9\end{align}\)
\(\begin{align}E(X^2) &= \displaystyle \frac{1}{17}(1^2 + 2^2 + \cdots + 17^2)\\& = \displaystyle \frac{1}{17} \cdot \frac{17(17 + 1)(2 \cdot 17 + 1)}{6} \\&= \displaystyle \frac{18 \cdot 35}{6} \\&= 105\end{align}\)
\(\begin{align}V(X) &= E(X^2) − \{E(X)\}^2 \\&= 105 − 9^2 \\&= 105 − 81 \\&= 24\end{align}\)
よって
\(\begin{align}E(2X + 5) &= 2E(X) + 5 \\&= 2 \cdot 9 + 5 \\&= 23\end{align}\)
\(\begin{align}V(2X + 5) &= 2^2 V(X) \\&= 4 \cdot 24 \\&= 96\end{align}\)
答え: \(E(2X + 5) = 23\)、\(V(2X + 5) = 96\)
計算問題③「\(E(X + 3Y)\), \(E(XY)\) を求める」
袋 \(A\) の中に赤玉 \(3\) 個、黒玉 \(2\) 個、袋 \(B\) の中に白玉 \(3\) 個、緑玉 \(2\) 個が入っている。\(A\) から玉 \(2\) 個同時に取り出したときの赤玉の個数を \(X\)、\(B\) から玉を \(2\) 個取り出したときの緑玉の個数を \(Y\) とするとき、\(X\), \(Y\) は確率変数である。このとき、期待値 \(E(X + 3Y)\) と \(E(XY)\) を求めよ。

\(E(X)\), \(E(Y)\) を求めてから、目的の期待値を求めましょう。\(E(XY)\) を求めるときは、「\(X\) と \(Y\) が独立であること」を必ず確認し、明記しましょう。
確率変数 \(X\), \(Y\) のとりうる値はともに \(0\), \(1\), \(2\) であり、\(X = k\), \(Y = i\) となる確率は
\(P(X = k) =\displaystyle \frac{{}_3 \mathrm{C}_k \cdot {}_2 \mathrm{C}_{2 − k}}{{}_5 \mathrm{C}_2} \ (k = 0, 1, 2)\)
\(P(Y = i) =\displaystyle \frac{{}_2 \mathrm{C}_i \cdot {}_3 \mathrm{C}_{2 − i}}{{}_5 \mathrm{C}_2} \ (i = 0, 1, 2)\)
よって \(X\), \(Y\) の確率分布はそれぞれ次のようになる。
|
\(X\) |
\(0\) |
\(1\) |
\(2\) |
計 |
|
\(P\) |
\(\displaystyle \frac{1}{10}\) |
\(\displaystyle \frac{6}{10}\) |
\(\displaystyle \frac{3}{10}\) |
\(1\) |
|
\(Y\) |
\(0\) |
\(1\) |
\(2\) |
計 |
|
\(P\) |
\(\displaystyle \frac{3}{10}\) |
\(\displaystyle \frac{6}{10}\) |
\(\displaystyle \frac{1}{10}\) |
\(1\) |
それぞれの期待値 \(E(X)\), \(E(Y)\) は
\(\begin{align}E(X) &= 0 \cdot \displaystyle \frac{1}{10} + 1 \cdot \displaystyle \frac{6}{10} + 2 \cdot \displaystyle \frac{3}{10} \\&= \displaystyle \frac{6}{5}\end{align}\)
\(\begin{align}E(Y) &= 0 \cdot \displaystyle \frac{3}{10} + 1 \cdot \displaystyle \frac{6}{10} + 2 \cdot \displaystyle \frac{1}{10} \\&= \displaystyle \frac{4}{5}\end{align}\)
よって、
\(\begin{align}E(X + 3Y) &= E(X) + 3E(Y) \\&= \displaystyle \frac{6}{5} + 3 \cdot \frac{4}{5} \\&= \frac{18}{5}\end{align}\)
また、\(X\) と \(Y\) は互いに独立であるから
\(\begin{align}E(XY) &= E(X)E(Y) \\&= \displaystyle \frac{6}{5} \cdot \frac{4}{5} \\&= \frac{24}{25}\end{align}\)
答え: \(E(X + 3Y) = \displaystyle \frac{18}{5}\)、\(E(XY) = \displaystyle \frac{24}{25}\)
以上で問題も終わりです!
確率分布の問題では、用語の意味・記号・公式をしっかり理解して、設問に応じて適切に立式する力が求められます。
確率の求め方がよくわからない…という人は、「場合の数と確率」を復習するところから始めてくださいね!
 場合の数と確率を総まとめ!数aで習う公式・法則一覧
場合の数と確率を総まとめ!数aで習う公式・法則一覧
