この記事では、「ベクトル方程式」をできるだけわかりやすく解説していきます。
直線、円といったさまざまな図形のベクトル方程式とそれぞれの問題の解き方を解説していきますので、この記事を通してぜひマスターしてくださいね。
目次
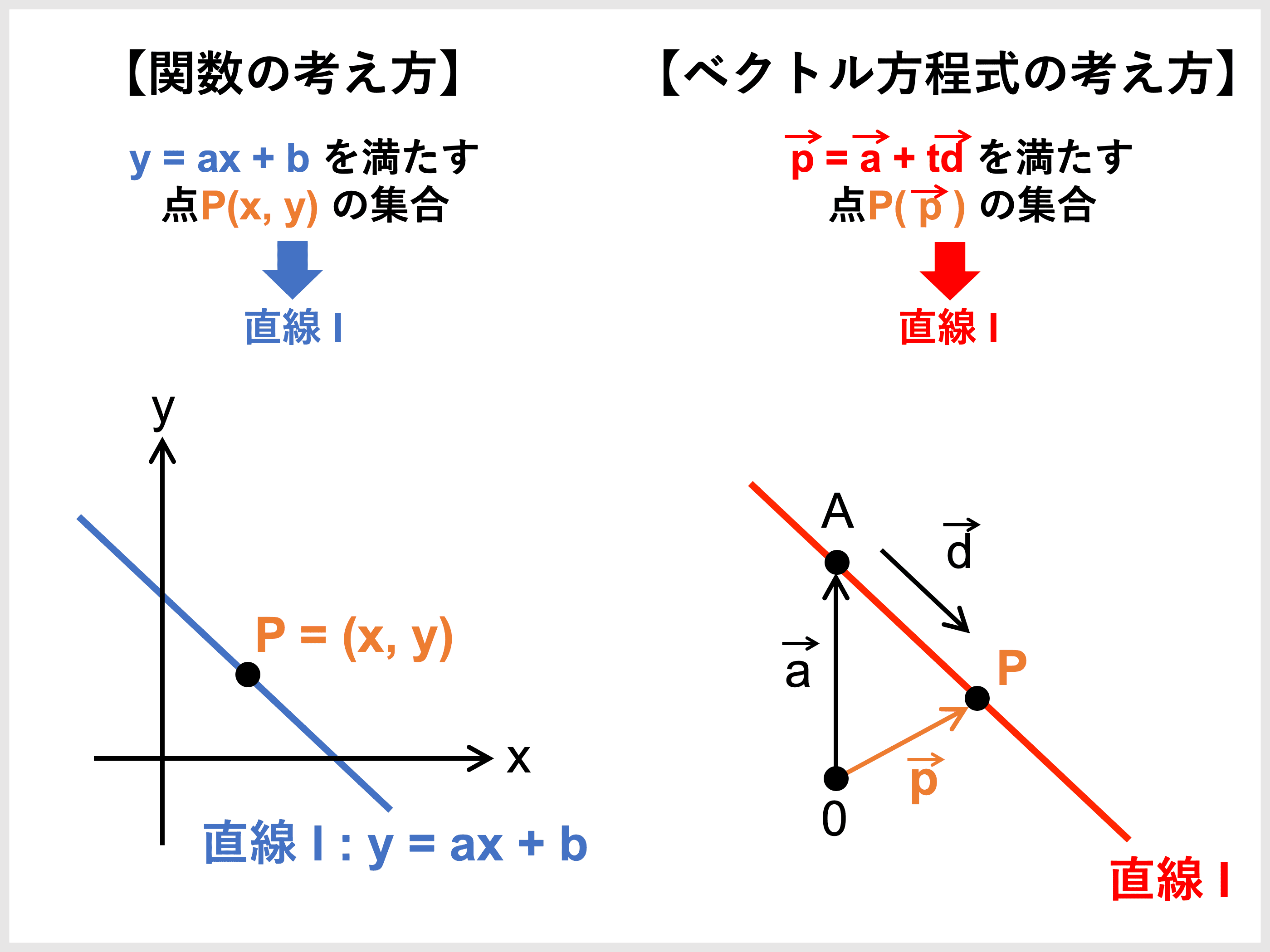
ベクトル方程式とは?
ベクトル方程式とは、平面上または空間内にある図形をベクトルで表現した式のことです。
さまざまな図形は、数学的には点の集合と見ることができます。
ベクトルでは、点の位置を表す「位置ベクトル」という便利なツールがあります。
この位置ベクトルを利用した、ある図形上の任意の点が満たす関係式を「ベクトル方程式」と呼びます。
次の章から、具体的なベクトル方程式の公式と問題の解き方を説明していきます。
【公式】直線のベクトル方程式
まずは、直線のベクトル方程式です。
一般的に、直線を特定するには「通る \(2\) 点」か「通る \(1\) 点と傾き」が定まればよいので、直線のベクトル方程式には次の \(3\) パターンがあります。
直線上の任意の点 \(\mathrm{P}\) の位置ベクトルを \(\vec{p}\) とし、\(s\), \(t\) を実数の変数とする。
[1] 通る \(\bf{2}\) 点がわかっている場合
異なる \(2\) 点 \(\mathrm{A}(\vec{a})\), \(\mathrm{B}(\vec{b})\) を通る直線のベクトル方程式は
\(\color{red}{\vec{p} = (1 − t)\vec{a} + t\vec{b}}\)
または
\(\color{red}{\vec{p} = s\vec{a} + t\vec{b} (s + t = 1)}\)
[2] 通る \(\bf{1}\) 点と平行なベクトルがわかっている場合
定点 \(\mathrm{A}(\vec{a})\) を通り、ベクトル \(\vec{d}\) に平行な直線のベクトル方程式は
\begin{align}\color{red}{\vec{p} = \vec{a} + t\vec{d}}\end{align}
(ただし、 \(\vec{d} \neq \vec{0}\) )
[3] 通る \(\bf{1}\) 点と垂直なベクトルがわかっている場合
定点 \(\mathrm{A}(\vec{a})\) を通り、ベクトル \(\vec{n}\) に垂直な直線のベクトル方程式は
\begin{align}\color{red}{\vec{n} \cdot (\vec{p} − \vec{a}) = 0}\end{align}
(ただし、\(\vec{n}\) は直線の法線ベクトル)
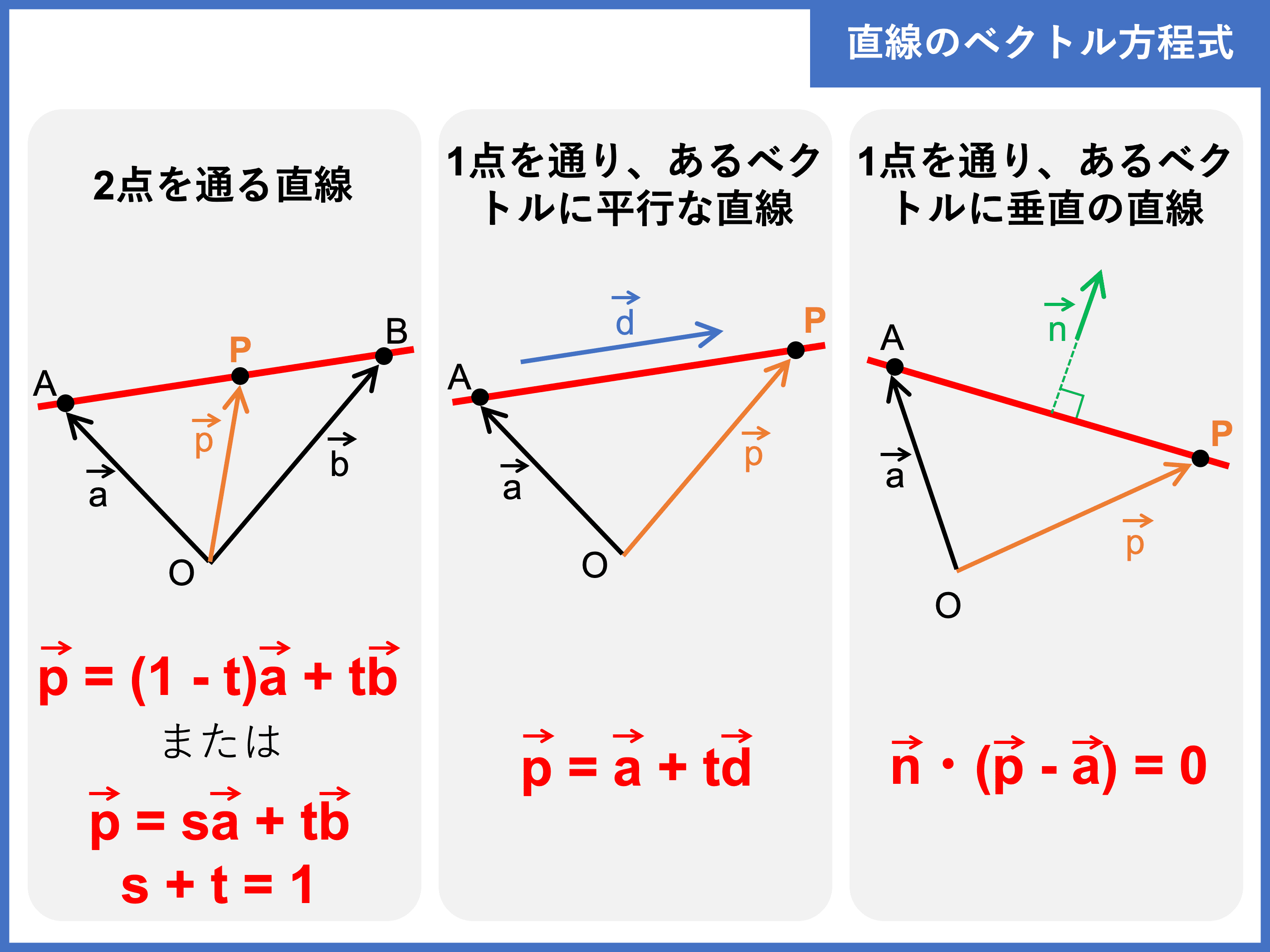
ある直線に平行なベクトルを「方向ベクトル」、垂直なベクトルを「法線ベクトル」といいます。
方向ベクトルは \(\vec{d}\)、法線ベクトルは \(\vec{n}\) と表すのが一般的です。
説明ばかりではなんだかよくわかりませんね。
例題を通して、直線のベクトル方程式への理解を深めましょう。
例題①「ある直線に平行な直線」
\(3\) 点 \(\mathrm{A}(\vec{a})\), \(\mathrm{B}(\vec{b})\), \(\mathrm{C}(\vec{c})\) を頂点にもつ \(\triangle \mathrm{ABC}\) がある。
辺 \(\mathrm{CA}\) を \(3 : 1\) に内分する点 \(\mathrm{M}(\vec{m})\) を通り、辺 \(\mathrm{AB}\) に平行な直線のベクトル方程式を求めよ。

問題文を見てもピンとこない場合は、とにかく図を描いてみましょう。
求めたい直線上に点 \(\mathrm{P}\) をとり、始点 \(\mathrm{O}\) からどこを通れば点 \(\mathrm{P}\) にたどり着くかな?と考えると、おのずとベクトル方程式が求められますよ。

\(\vec{m}\) は辺 \(\mathrm{CA}\) を \(3 : 1\) に内分するから、
\(\vec{m} = \displaystyle \frac{\vec{c} + 3\vec{a}}{3 + 1} = \frac{\vec{c} + 3\vec{a}}{4}\)
求める直線上の点を \(\mathrm{P}(\vec{p})\)、\(\overrightarrow{\mathrm{MP}} = t\overrightarrow{\mathrm{AB}}\)(\(t\) は実数の変数)とおくと、
\(\begin{align}\vec{p} &= \overrightarrow{\mathrm{OM}} + \overrightarrow{\mathrm{MP}} \\ &= \vec{m} + t\overrightarrow{\mathrm{AB}}\\ &= \displaystyle \frac{\vec{c} + 3\vec{a}}{4} + t(\vec{b} − \vec{a})\\ &= \displaystyle \frac{1}{4} \vec{c} + \frac{3}{4} \vec{a} + t\vec{b} − t\vec{a} \\ &= \displaystyle \left( \frac{3}{4} − t \right) \vec{a} + t\vec{b} + \frac{1}{4} \vec{c} \end{align}\)
答え: \(\color{red}{\displaystyle \left( \frac{3}{4} − t \right) \vec{a} + t\vec{b} + \frac{1}{4} \vec{c}}\)
例題②「2 点を通る直線」
\(2\) 点 \(\mathrm{A}(2, 3)\), \(\mathrm{B}(−1, 8)\) を通る直線の方程式を媒介変数 \(t\) を用いて表せ。
また、\(t\) を消去した式で表せ。

\(2\) 点の成分が与えられているので、\(2\) 点を通る直線のベクトル方程式 \(\vec{p} = (1 − t)\vec{a} + t\vec{b}\) に成分を代入して計算を進めましょう。
求める直線上の点を \(\mathrm{P}(x, y)\) とする。

\(\overrightarrow{\mathrm{OP}} = (1 − t)\overrightarrow{\mathrm{OA}} + t\overrightarrow{\mathrm{OB}}\) より、
\(\begin{align} (x, y) &= (1 − t)(2, 3) + t(−1, 8) \\ &= (2 − 2t, 3 − 3t) + (−t, 8t) \\ &= (2 − 3t, 3 + 5t) \end{align}\)
より、
\(\left\{\begin{array}{l} x = 2 − 3t \text{…①}\\ y = 3 + 5t \text{…②}\end{array}\right.\)
①より
\(3t = 2 − x\)
\(\displaystyle t = \frac{1}{3}(2 − x)\)
②に代入して
\(\begin{align} y &= 3 + \frac{5}{3}(2 − x) \\ &= 3 + \frac{10}{3} − \frac{5}{3}x \\ &= −\frac{5}{3}x + \frac{19}{3} \end{align}\)
答え:
\(t\) あり \((x, y) = (2 − 3t, 3 + 5t)\)
\(t\) なし \(\displaystyle y = −\frac{5}{3}x + \frac{19}{3}\)
例題③「1 点と法線ベクトルがわかる直線」
点 \((2, −1)\) を通り、\(\vec{n} = (3, 4)\) に垂直な直線の方程式を求めよ。

法線ベクトルから直線の方程式を求める問題です。
直線上の点を \(\mathrm{P}(x, y)\) として式を立ててみましょう。
通る点を \(\mathrm{A}(2, −1)\) 、求める直線上の点を \(\mathrm{P}(x, y)\) とすると、
求める直線のベクトルは
\(\overrightarrow{\mathrm{AP}} = (x − 2, y − (−1)) = (x − 2, y + 1)\)
これが \(\vec{n} = (3, 4)\) と垂直に交わるから、
\(\overrightarrow{\mathrm{AP}} \cdot \vec{n} = 0\)
すなわち
\((x − 2) \cdot 3 + (y + 1) \cdot 4 = 0\)
\(3x − 6 + 4y + 4 = 0\)
\(3x + 4y − 2 = 0\)
したがって、求める直線の方程式は \(3x + 4y − 2 = 0\)
答え: \(\color{red}{3x + 4y − 2 = 0}\)
【公式】円のベクトル方程式
円のベクトル方程式には次の \(2\) パターンがあります。
\(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\), \(\overrightarrow{\mathrm{OC}} = \vec{c}\), \(\overrightarrow{\mathrm{OP}} = \vec{p}\) とし、\(\mathrm{P}\) は円周上の任意の点とする。
[1] 中心が点 \(\bf{C}\)、半径 \(\bf{r}\) の円
\(\color{red}{|\vec{p} − \vec{c}| = r}\)
または
\(\color{red}{(\vec{p} − \vec{c}) \cdot (\vec{p} − \vec{c}) = r^2}\)
[2] 線分 \(\bf{AB}\) を直径とする円
\begin{align}\color{red}{(\vec{p} − \vec{a}) \cdot (\vec{p} − \vec{b}) = 0}\end{align}
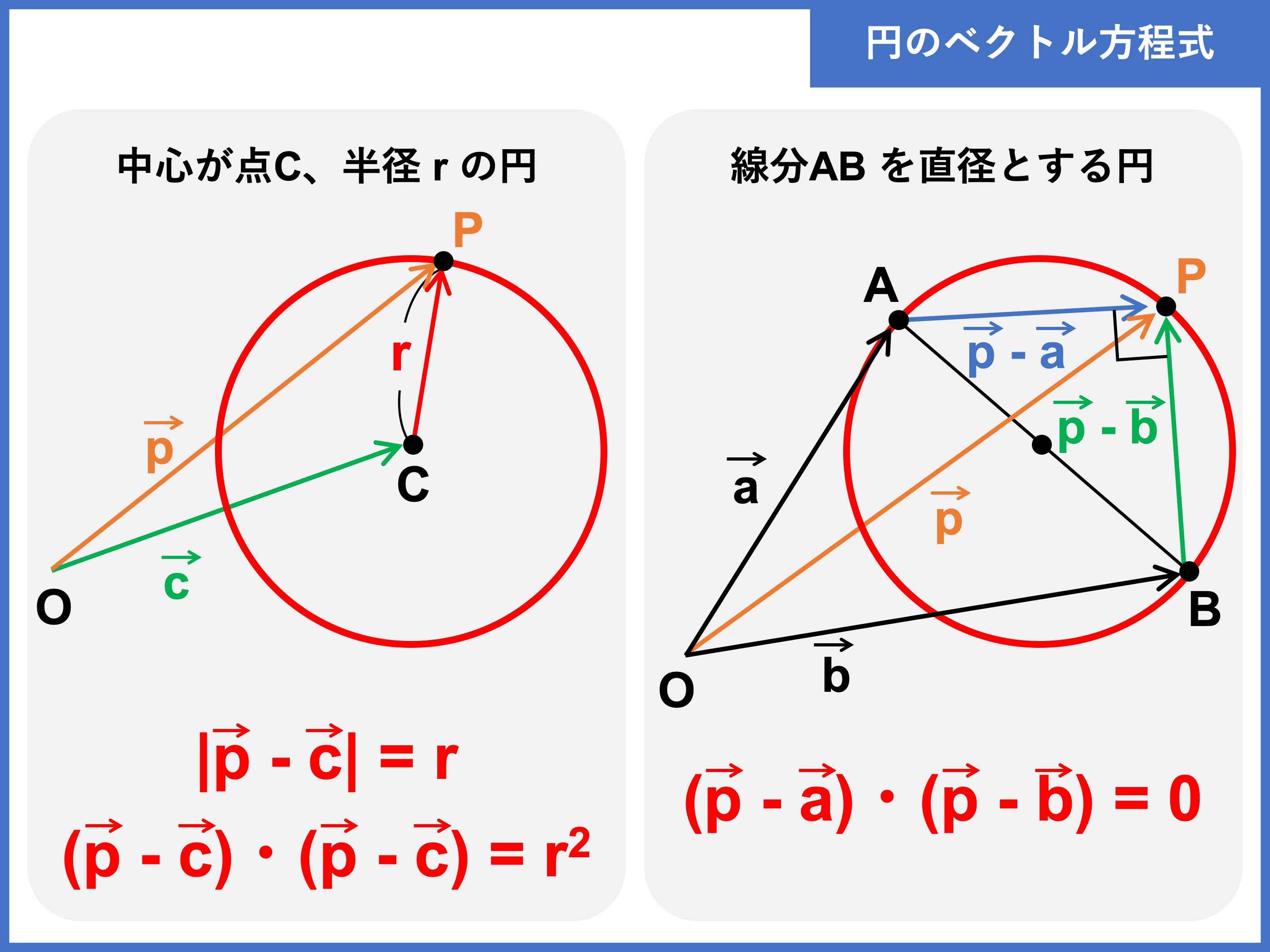
\(1\) つ目は、円周上の点から中心への距離が半径に等しいことから導かれる式ですね。
\(2\) つ目は、直径に対する円周角が常に \(90^\circ\) 、つまり「\(\overrightarrow{\mathrm{AP}} \perp \overrightarrow{\mathrm{BP}}\)」となることを利用した内積の垂直条件の式です。
それでは、例題を見てみましょう。
例題「ベクトル方程式から図形を求める」
平面上の異なる \(2\) つの定点 \(\mathrm{A}\), \(\mathrm{B}\) と任意の点 \(\mathrm{P}\) に対し、\(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\), \(\overrightarrow{\mathrm{OP}} = \vec{p}\) とする。
ベクトル方程式 \(|3\vec{a} + 2\vec{b} − 5\vec{p}| = 10\) はどのような図形を表すか。

左辺がベクトルの絶対値で右辺が数値ということは、あるベクトルの大きさが常に一定ということです。
このような場合は、円のベクトル方程式を疑います。
円のベクトル方程式 \(|\vec{p} − \vec{c}| = r\) の形になるように、式を変形していきましょう。
\(|3\vec{a} + 2\vec{b} − 5\vec{p}| = 10\) を変形すると
\(\displaystyle \left| −5\vec{p} + 5 \cdot \frac{3\vec{a} + 2\vec{b}}{5} \right| = 10\)
\(\displaystyle 5\left| \vec{p} − \frac{3\vec{a} + 2\vec{b}}{5} \right| = 10\)
\(\displaystyle \left| \vec{p} − \frac{3\vec{a} + 2\vec{b}}{5} \right| = 2\)
よって、線分 \(\mathrm{AB}\) を \(2 : 3\) に内分する点を中心とする半径 \(2\) の円を表す。

答え: 線分 \(\mathrm{AB}\) を \(2 : 3\) に内分する点を中心とする半径 \(2\) の円
【公式】球面のベクトル方程式
実は、空間ベクトルにおける球面のベクトル方程式も、平面上の円のベクトル方程式とまったく同じ式になります。
\(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\), \(\overrightarrow{\mathrm{OC}} = \vec{c}\), \(\overrightarrow{\mathrm{OP}} = \vec{p}\) とし、\(\mathrm{P}\) は球面上の任意の点とする。
[1] 中心が点 \(\bf{C}\)、半径 \(\bf{r}\) の球面
\(\color{red}{|\vec{p} − \vec{c}| = r}\)
または
\(\color{red}{(\vec{p} − \vec{c}) \cdot (\vec{p} − \vec{c}) = r^2}\)
[2] 線分 \(\bf{AB}\) を直径とする球面
\begin{align}\color{red}{(\vec{p} − \vec{a}) \cdot (\vec{p} − \vec{b}) = 0}\end{align}
点 \(\mathrm{C}\), \(\mathrm{P}\) の \(2\) 点、または点 \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{P}\) の \(3\) 点だけに注目するので、それらの点を通る平面で球を切り開くと、平面上の円と同じように考えることができますね。
それでは、例題に挑戦しましょう。
例題「球面のベクトル方程式を求める」
\(2\) 点 \(\mathrm{O}(\vec{o})\), \(\mathrm{A}(\vec{a})\) を直径の両端とする球面のベクトル方程式を求めよ。

球面であっても、円のベクトル方程式と同じなのでしたね。
始点 \(\mathrm{O}\) が球面上にあることに留意しながら、ベクトル方程式を導きましょう。

求める球面上の点を \(\mathrm{P}(\vec{p})\) とおくと、
\(\mathrm{OP} \perp \mathrm{AP}\) より、
\(\vec{p} \cdot (\vec{p} − \vec{a}) = 0\)
答え: \(\color{red}{\vec{p} \cdot (\vec{p} − \vec{a}) = 0}\)
【公式】平面上の点の存在範囲
平面上のベクトルが異なる \(2\) つのベクトルに分解できることを利用すると、ある点が平面上のどのような位置に存在するかを調べることができます。
点の存在範囲となりうる代表的な図形は以下のとおりです。
\(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\), \(\overrightarrow{\mathrm{OP}} = \vec{p}\) とする。
(ただし、\(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\), \(\vec{a} \neq \vec{b}\)、\(s\) と \(t\) は実数の変数とする。)
\(\color{red}{\vec{p} = s\vec{a} + t\vec{b}}\) について、\(s\), \(t\) に条件があると、\(\vec{p}\) の終点 \(\mathrm{P}\) の存在範囲は次のようになる。
[1] 直線 \(\bf{AB}\)
\begin{align}\color{red}{s + t = 1}\end{align}
[2] 線分 \(\bf{AB}\)
\begin{align}\color{red}{s + t = 1, s \geq 0, t \geq 0}\end{align}
[3] \(\bf{\triangle OAB}\) の周および内部
\begin{align}\color{red}{s + t \leq 1, s \geq 0, t \geq 0}\end{align}
[4] 平行四辺形 \(\bf{OACB}\) の周および内部
\begin{align}\color{red}{0 \leq s \leq 1, 0 \leq t \leq 1}\end{align}
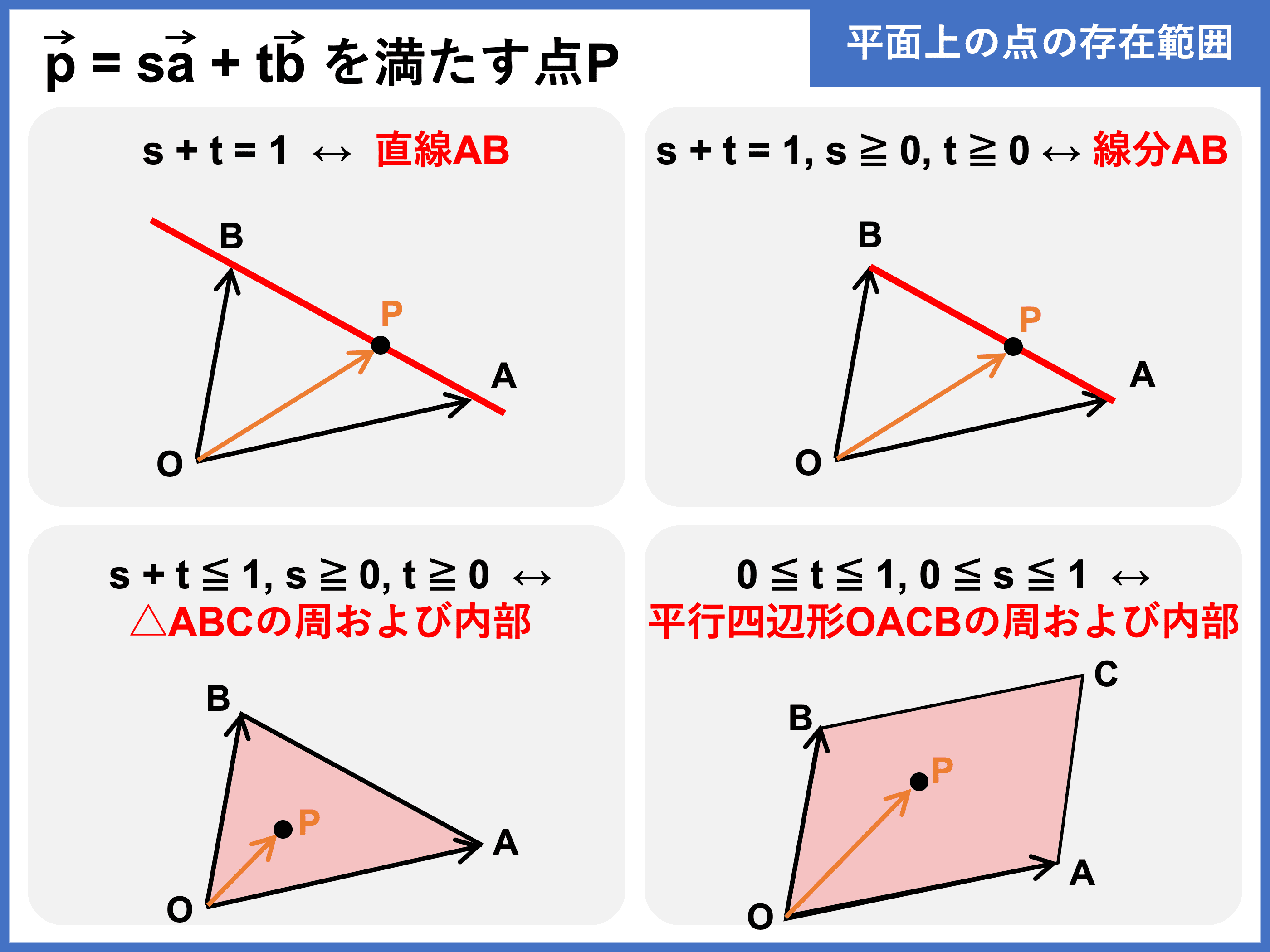
ベクトル \(\vec{p}\) を \(s\) 倍した \(\vec{a}\) と \(t\) 倍した \(\vec{b}\) の和に分解すると、\(s\) と \(t\) がとる値の範囲から、\(\vec{p}\) の終点 \(\mathrm{P}\) が存在する範囲を特定できます。
問題でよく登場する存在範囲は上記のとおりですが、\(s\), \(t\) の値を変えれば平面上に存在するあらゆる点を自由自在に表現できます。
\(s\) や \(t\) の値と点の存在範囲の関係は次のようになっています。
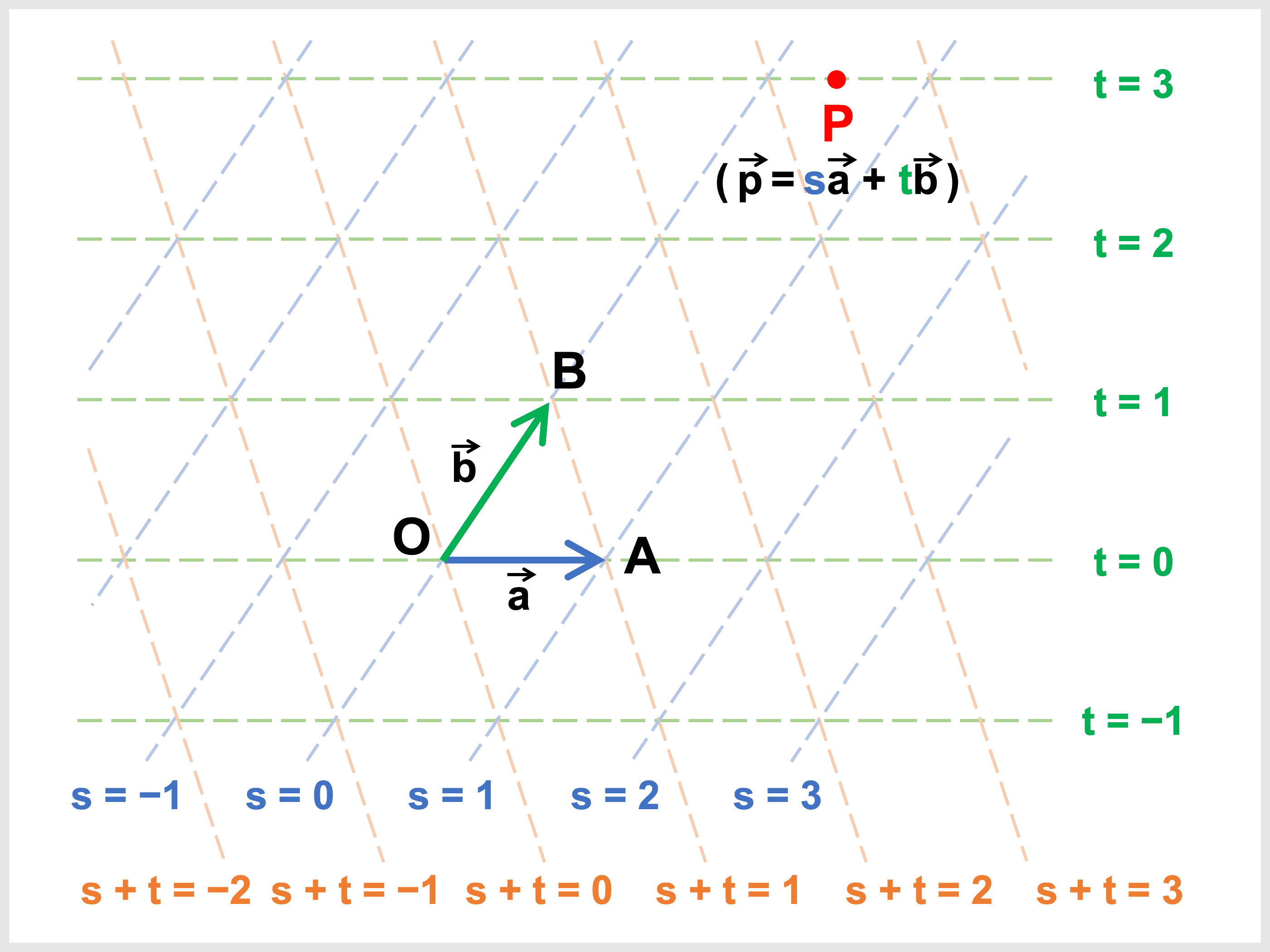
覚える必要はまったくありませんが、なんとなくこういう規則で \(s\), \(t\) と点の存在範囲が連動しているんだな〜という感覚をつかんでみてください!
例題①「s + t ≠ 1 の点の存在範囲」
\(\triangle \mathrm{OAB}\) に対し、\(\overrightarrow{\mathrm{OP}} = s\overrightarrow{\mathrm{OA}} + t\overrightarrow{\mathrm{OB}}\)(\(s\), \(t\) は実数)とする。
\(s\), \(t\) が次の条件を満たしながら変化するとき、点 \(\mathrm{P}\) の描く図形を図示せよ。
\(s + t = 3\), \(s \geq 0\), \(t \geq 0\)

\(s\) と \(t\) の和が \(1\) 以外の場合なんて習っていないよ!と思うかもしれませんね。
そんなときは、和が \(1\) になるように \(s + t = 3\) を無理やり変形し、計算を進めましょう。
そうすると、新しい図形が見えてきますよ。
\(s + t = 3\) より、
\(\displaystyle \frac{s}{3} + \frac{t}{3} = 1\)
\(\begin{align} \overrightarrow{\mathrm{OP}} &= s\overrightarrow{\mathrm{OA}} + t\overrightarrow{\mathrm{OB}} \\ &= \frac{s}{3} (3\overrightarrow{\mathrm{OA}}) + \frac{t}{3} (3\overrightarrow{\mathrm{OB}}) \end{align}\)
ここで、\(\displaystyle \frac{s}{3} = s’\)、\(\displaystyle \frac{t}{3} = t’\)、\(3\overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{OA’}}\)、\(3\overrightarrow{\mathrm{OB}} = \overrightarrow{\mathrm{OB’}}\) とおくと、
\(\overrightarrow{\mathrm{OP}} = s’\overrightarrow{\mathrm{OA’}} + t’\overrightarrow{\mathrm{OB’}}\)
\(s’ + t’ = 1\) , \(s’ \geq 0\) , \(t’ \geq 0\)

よって、点 \(\mathrm{P}\) が描く図形は線分 \(\mathrm{A’B’}\)
答え:

例題②「s + t の不等式と点の存在範囲」
\(\mathrm{O}\) を原点、\(\mathrm{A}(2, 1)\), \(\mathrm{B}(1, 2)\)、\(\overrightarrow{\mathrm{OP}} = s\overrightarrow{\mathrm{OA}} + t\overrightarrow{\mathrm{OB}}\)(\(s\), \(t\) は実数)とする。
\(s\), \(t\) が次の関係を満たしながら変化するとき、点 \(\mathrm{P}\) の描く図形を図示せよ。
\(1 \leq s + t \leq 2\) , \(s \geq 0\) , \(t \geq 0\)

\(s\), \(t\) のどちらにも範囲の幅があるはずなので、このままだと考えにくいですね。
このような場合は、次の考え方で進めていきましょう。
- \(s + t = k\) とおく
- まず \(k\) を固定し、\(s\), \(t\) を動かす(点 \(\mathrm{P}\) が動ける図形の範囲を定める)
- \(k\) を動かす(1 の図形が動ける範囲を定める)
\(s + t = k\) とすると、
\(\displaystyle \frac{s}{k} + \frac{t}{k} = 1\)
\(1 \leq k \leq 2\)
\(k\overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{OQ}}\)、\(k\overrightarrow{\mathrm{OB}} = \overrightarrow{\mathrm{OR}}\) とおくと、
\(\begin{align} \overrightarrow{\mathrm{OP}} &= s\overrightarrow{\mathrm{OA}} + t\overrightarrow{\mathrm{OB}} \\ &= \frac{s}{k} \overrightarrow{\mathrm{OQ}} + \frac{t}{k} \overrightarrow{\mathrm{OR}} \end{align}\)
\(\displaystyle \frac{s}{k} + \frac{t}{k} = 1\), \(\displaystyle \frac{s}{k} \geq 0\), \(\displaystyle \frac{t}{k} \geq 0\)
よって、点 \(\mathrm{P}\) は線分 \(\mathrm{QR}\) 上を動く。

さらに、\(k\) を \(1 \leq k \leq 2\) の範囲で動かすと、点 \(\mathrm{Q}\) は下図の線分 \(\mathrm{AA’}\) 上を動く。

よって、点 \(\mathrm{P}\) は四角形 \(\mathrm{ABB’A’}\) の周上および内部を動く。
答え: 図の赤く塗りつぶした部分(境界線含む)。

【公式】空間ベクトルの共面条件
異なる \(4\) つの空間ベクトルの終点が同じ平面上にある条件を、「共面条件」といいます。
点 \(\mathrm{P}(\vec{p})\) が、同一直線上にない \(3\) 点 \(\mathrm{A}(\vec{a})\), \(\mathrm{B}(\vec{b})\), \(\mathrm{C}(\vec{c})\) の定める平面上にある
\(\iff \color{red}{\overrightarrow{\mathrm{AP}} = s\overrightarrow{\mathrm{AB}} + t\overrightarrow{\mathrm{AC}}}\) となる実数 \(\color{red}{s, t}\) がある
\(\iff \color{red}{\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}}\) となる実数 \(\color{red}{s, t, u}\) で \(\color{red}{s + t + u = 1}\) を満たすものがある
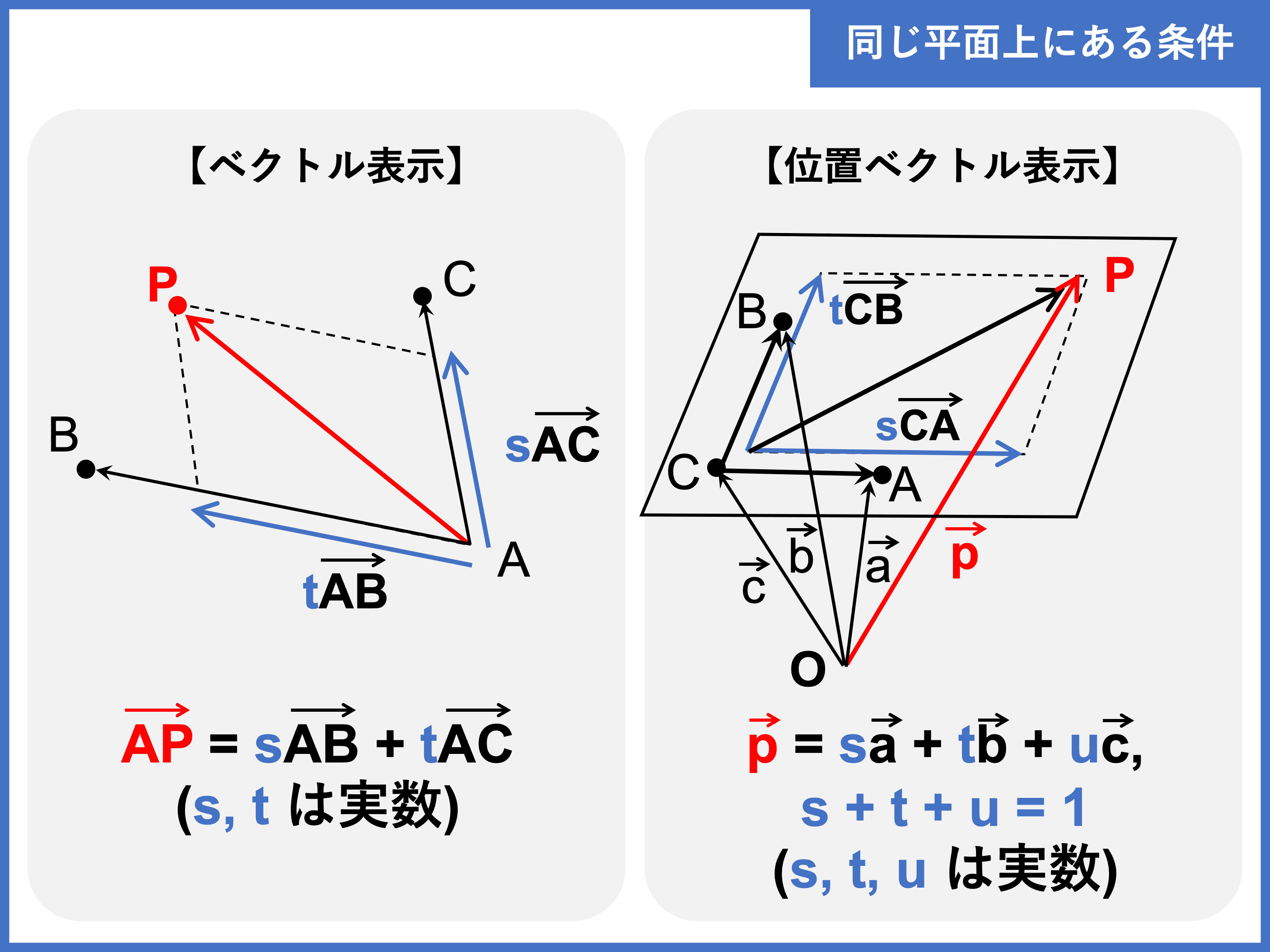
考え方としては先ほどの点の存在範囲と同じです。
同じ平面上にあればよいので、実数 \(s\), \(t\)(または \(u\))が存在することさえ示せれば範囲は絞らなくてよいのです。
例題「4 点が同一平面上にあることを利用」
共面条件を利用する問題の解き方を確認しましょう。
\(4\) 点 \(\mathrm{A}(3, 1, 0)\), \(\mathrm{B}(2, 4, 1)\), \(\mathrm{C}(1, 0, −1)\), \(\mathrm{P}(x, 8, 1)\) が同一平面上にあるとき、定数 \(x\) の値を求めよ。

異なる \(4\) 点が同じ平面上にある条件から、式を立てましょう。
その前に、\(\mathrm{P}\) 以外の \(3\) 点がちゃんと平面をなしていること(同一直線上にないこと)を確認しておくことに注意です。
\(\begin{align} \overrightarrow{\mathrm{AC}} &= (1, 0, −1) − (3, 1, 0) \\ &= (−2, −1, −1) \end{align}\)
\(\begin{align} \overrightarrow{\mathrm{AB}} &= (2, 4, 1) − (3, 1, 0) \\ &= (−1, 3, 1) \end{align}\)
より、\(\overrightarrow{\mathrm{AC}} = k\overrightarrow{\mathrm{AB}}\) を満たす実数 \(k\) は存在しないから、\(3\) 点 \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\) は一直線上にない。
点 \(\mathrm{P}\) が平面 \(\mathrm{ABC}\) 上にある条件は、
\(\overrightarrow{\mathrm{AP}} = s\overrightarrow{\mathrm{AB}} + t\overrightarrow{\mathrm{AC}}\)
となる実数 \(s\), \(t\) が存在することである。
\(\begin{align} \overrightarrow{\mathrm{AP}} &= (x, 8, 1) − (3, 1, 0) \\ &= (x − 3, 7, 1) \end{align}\)
より
\((x − 3, 7, 1) = s(−1, 3, 1) + t(−2, −1, −1)\)
\((x − 3, 7, 1) = (−s − 2t, 3s − t, s − t)\)
よって
\(\left\{\begin{array}{l} x − 3 = −s − 2t \text{…①}\\ 7 = 3s − t \text{…②}\\ 1 = s − t \text{…③}\end{array}\right.\)
② − ③より、
\(6 = 2s\)
\(s = 3\)
\(t = s − 1 = 3 − 1 = 2\)
①より
\(\begin{align} x &= −s − 2t + 3 \\ &= −3 − 4 + 3 \\ &= −4 \end{align}\)
答え: \(\color{red}{x = −4}\)
【公式】平面のベクトル方程式
三次元空間に存在する平面のベクトル方程式には次の \(2\) パターンがあります。
\(\mathrm{P}\) は平面上の任意の点とし、\(s\), \(t\), \(u\) を実数の変数とする。
[1] 同じ直線上にない \(\bf{3}\) 点 \(\bf{A(\vec{a})}\), \(\bf{B(\vec{b})}\), \(\bf{C(\vec{c})}\) を通る平面
\begin{align}\color{red}{\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}, s + t + u = 1}\end{align}
[2] 点 \(\bf{A(\vec{a})}\) を通り、\(\bf{\vec{0}}\) でないベクトル \(\bf{\vec{n}}\) に垂直な平面
\begin{align}\color{red}{\vec{n} \cdot (\vec{p} − \vec{a}) = 0}\end{align}
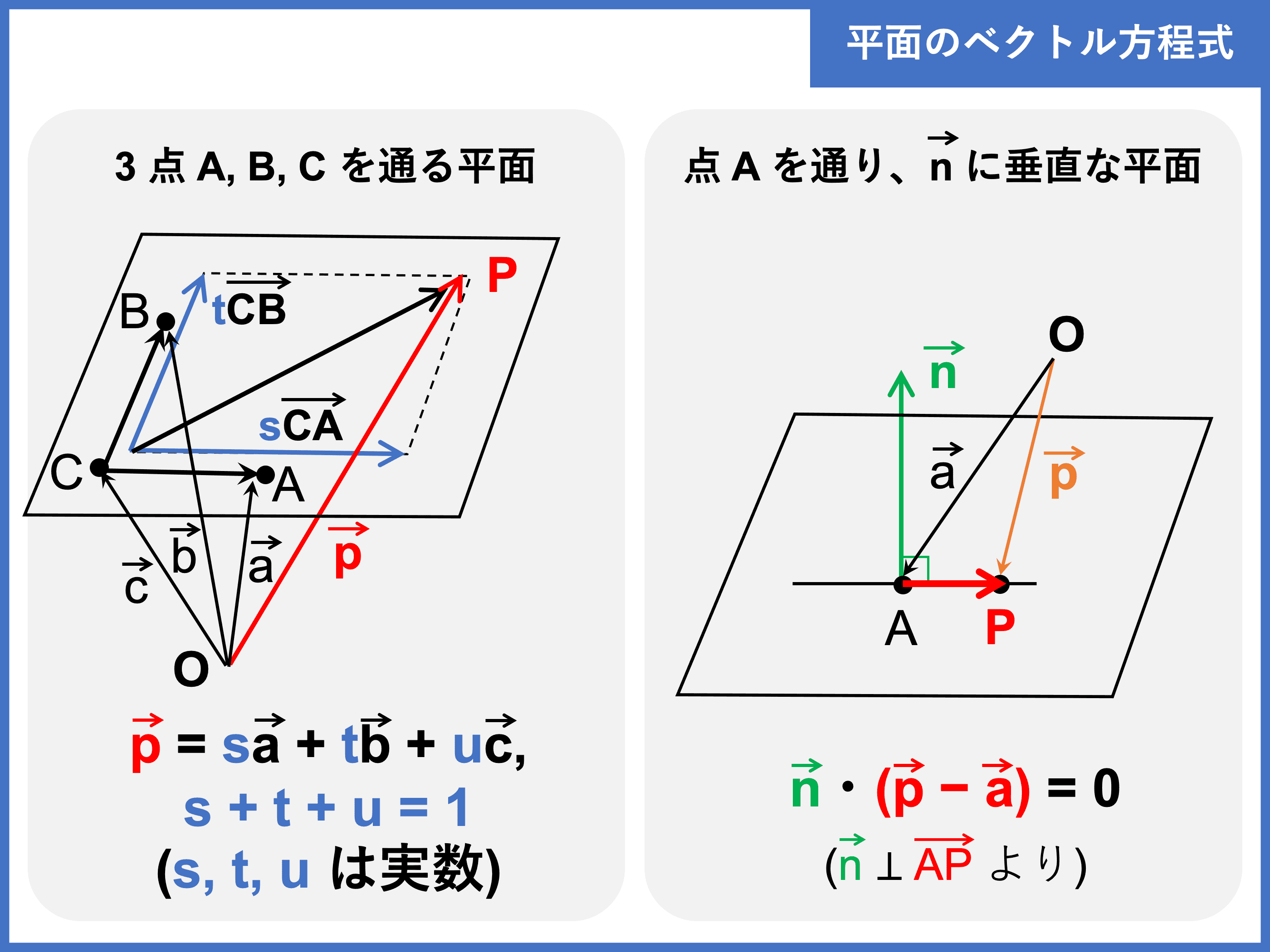
例題「平面の方程式を求める」
\(3\) 点 \(\mathrm{A}(1, 0, 2)\), \(\mathrm{B}(0, 1, 0)\), \(\mathrm{C}(2, 1, −3)\) を通る平面の方程式を求めよ。

平面の方程式の公式 \(ax + by + cz + d = 0\) から求めることもできますが、ここでは平面のベクトル方程式 [2] で法線ベクトルを利用する方法を説明します。
求める平面の法線ベクトルを \(\vec{n} = (a, b, c)\) とする。
\(\begin{align} \overrightarrow{\mathrm{AB}} &= (0, 1, 0) − (1, 0, 2) \\ &= (−1, 1, −2) \end{align}\)
\(\begin{align} \overrightarrow{\mathrm{AC}} &= (2, 1, −3) − (1, 0, 2) \\ &= (1, 1, −5) \end{align}\)
であるから、
\(\begin{align}\vec{n} \perp \overrightarrow{\mathrm{AB}} &\iff \vec{n} \cdot \overrightarrow{\mathrm{AB}} = 0 \\ &\iff −a + b − 2c = 0 \cdots ①\end{align}\)
\(\begin{align}\vec{n} \perp \overrightarrow{\mathrm{AC}} &\iff \vec{n} \cdot \overrightarrow{\mathrm{AC}} = 0 \\ &\iff a + b − 5c = 0 \cdots ②\end{align}\)
\(① − ②\) より
\(−2a + 3c = 0\) すなわち \(c = \displaystyle \frac{2}{3}a\)
\(① \times 5 − ② \times 2\) より
\(−7a + 3b = 0\) すなわち \(b = \displaystyle \frac{7}{3}a\)
そこで、\(\vec{n} = (3, 7, 2)\) とする。
求める平面は、点 \(\mathrm{A}(1, 0, 2)\) を通り \(\vec{n} = (3, 7, 2)\) に垂直であるから、
平面上の任意の点を \(\mathrm{P}(x, y, z)\) とおくと
\(\begin{align}\vec{n} \perp \overrightarrow{\mathrm{AP}} &\iff \vec{n} \cdot \overrightarrow{\mathrm{AP}} = 0 \\ & \iff \vec{n} \cdot (\vec{p} − \vec{a}) = 0\end{align}\)
\(\begin{align}\vec{p} − \vec{a} &= (x, y, z) − (1, 0, 2) \\&= (x − 1, y, z − 2)\end{align}\)
より、求める平面の方程式は
\(3(x − 1) + 7y + 2(z − 2) = 0\)
\(3x − 3 + 7y + 2z − 4 = 0\)
すなわち
\(3x + 7y + 2z − 7 = 0\)
答え: \(\color{red}{3x + 7y + 2z − 7 = 0}\)
ここまでで、さまざまなベクトル方程式をご紹介してきました。いかがでしたか?
ベクトル方程式は種類も多く、丸暗記しようと思うととても負担になります。
どういう考えでベクトル方程式が立つかを理解し、あとはとにかくたくさんの問題を解いて慣れていきましょう!
ベクトルに関するほかの公式や問題について調べたい方は、以下のまとめ記事から探してみてくださいね!
 ベクトルを総まとめ!高校で習う公式一覧
ベクトルを総まとめ!高校で習う公式一覧




例題 平面の方程式を求める
の解答で
3(x−1)+7y−2(z−2)=0
となっている式は間違いで
正しくは
3(x−1)+7y+2(z−2)=0
より答え3x+7y+2z=0
ではありませんか?
コメントありがとうございます。
ご指摘のとおり、途中式の符号が誤っていたようです。該当部分を修正いたしました。
このようにご指摘いただけるととても助かります。
今後ともどうぞ当サイトをよろしくお願いいたします。