この記事では、ベクトルの「平行条件」と「垂直条件」をできるだけわかりやすく解説していきます。
計算問題や証明問題の解き方も解説していきますので、この記事を通してぜひマスターしてくださいね。
目次
ベクトルの平行条件「\(\vec{a} = k\vec{b}\)」
\(2\) つのベクトルが平行であるための条件を「ベクトルの平行条件」といいます。
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a}\), \(\vec{b}\) に対して、
\(\vec{a} \ // \ \vec{b} \iff \vec{a} = k \vec{b}\) となる実数 \(k\) がある
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a}\) と \(\vec{b}\) が平行であるとき、\(\vec{b}\) は平行移動によって \(\vec{a}\) が定める直線上に移すことができます。
そして、移動した \(\vec{b}\) は適当な大きさに拡大または縮小すると \(\vec{a}\) に一致させることができます。
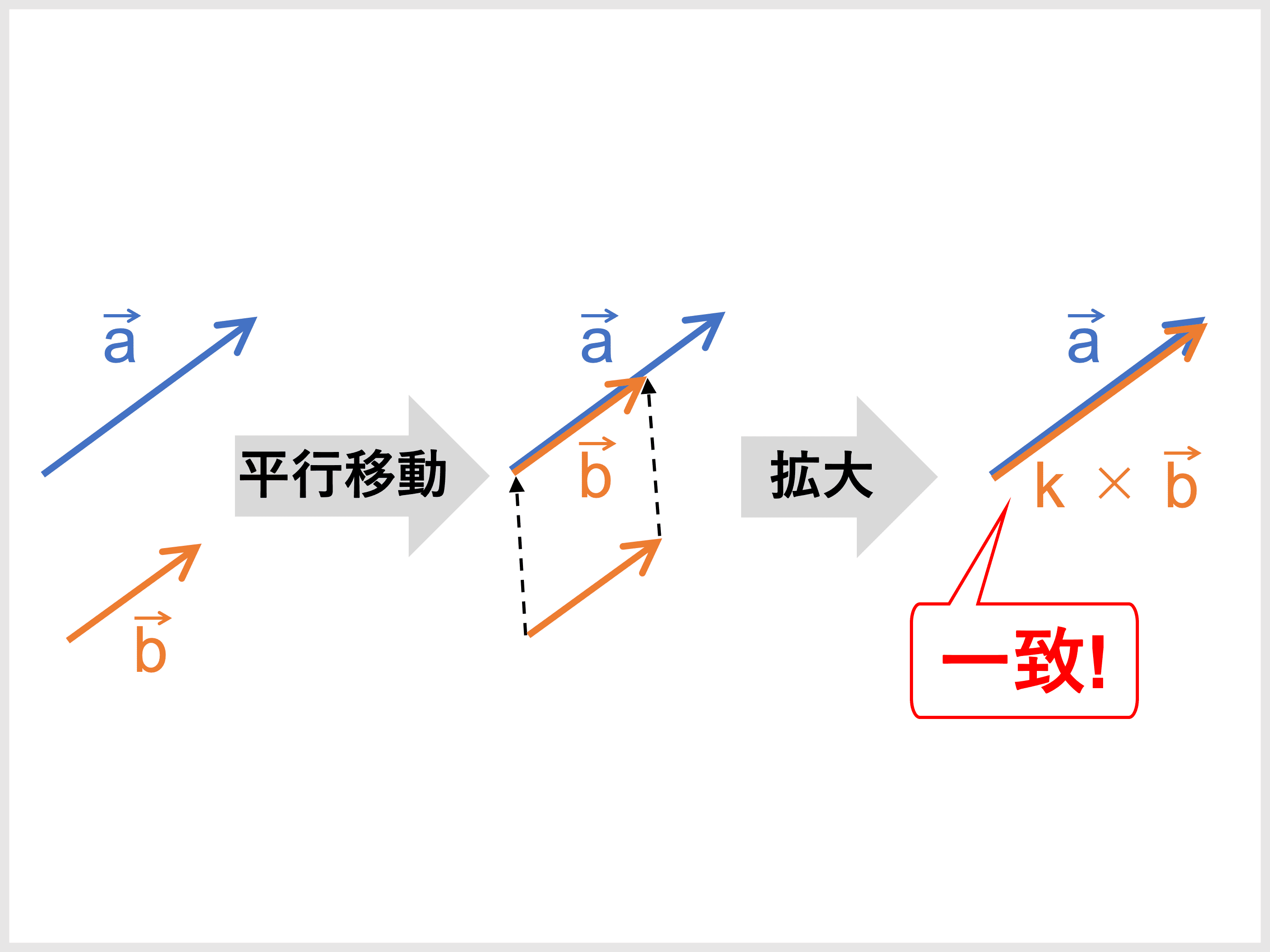
だから、任意の実数 \(k\) を使って \(\vec{a} = k \vec{b}\) と表せるのですね。
平行条件は平面ベクトルであろうと空間ベクトルであろうと共通ですが、成分表示では式が異なります。
平面ベクトルの平行条件
平面ベクトル(二次元)における平行条件は、次のように表せます。
\(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\)(ただし \(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\))のとき、
\begin{align}\vec{a} \ // \ \vec{b} &\iff \vec{a} = k \vec{b} \ \text{となる実数} \ k \ \text{がある} \\ &\iff \color{red}{a_1b_2 − a_2b_1 = 0 \ \text{(成分表示)}}\end{align}
最初の条件式 \(\vec{a} = k \vec{b}\) から、\((a_1, a_2) = k(b_1, b_2)\) となる \(k\) を探すことでも平行は示せます(詳しくは計算問題①で解説)。
\(2\) つのベクトルが平行ということは、それぞれの \(x\), \(y\) 成分の比は等しくなります。
\(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\) が平行であるとき、
\(a_1 : a_2 = b_1 : b_2\) より
\(a_1b_2 = a_2b_1\)
したがって、
\(\color{red}{\vec{a} \ // \ \vec{b} \iff a_1 b_2 − a_2 b_1 = 0}\)
空間ベクトルの平行条件
空間ベクトル(三次元)における平行条件は、次のように表せます。
\(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\)(ただし \(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\))のとき、
\begin{align}\vec{a} \ // \ \vec{b} &\iff \vec{a} = k \vec{b} \ \text{となる実数} \ k \ \text{がある} \\ &\iff \color{red}{\left\{\begin{array}{l} a_1 b_2 − a_2 b_1 = 0 \\ a_2b_3 − a_3b_2 = 0 \\ a_3b_1 − a_1b_3 = 0 \end{array}\right. \ \text{(成分表示)}}\end{align}
最初の条件式 \(\vec{a} = k \vec{b}\) から、\((a_1, a_2, a_3) = k(b_1, b_2, b_3)\) となる \(k\) を探すことでも平行を示すことができるので、成分表示の公式は無理に覚えなくても大丈夫です。
\(2\) つの空間ベクトルが平行ということは、それぞれの \(x\), \(y\), \(z\) 成分の比は等しくなります。
\(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\) が平行であるとき、
\(a_1 : a_2 : a_3 = b_1 : b_2 : b_3\)
\(a_1 : a_2 = b_1 : b_2\) より
\(a_1b_2 = a_2b_1\) すなわち \(a_1 b_2 − a_2 b_1 = 0\)
\(a_2 : a_3 = b_2 : b_3\) より
\(a_2b_3 = a_3b_2\) すなわち \(a_2 b_3 − a_3 b_2 = 0\)
\(a_3 : a_1 = b_3 : b_1\) より
\(a_3b_1 = a_1b_3\) すなわち \(a_3 b_1 − a_1 b_3 = 0\)
したがって、
\(\color{red}{\vec{a} \ // \ \vec{b} \iff \left\{\begin{array}{l} a_1 b_2 − a_2 b_1 = 0 \\ a_2b_3 − a_3b_2 = 0 \\ a_3b_1 − a_1b_3 = 0 \end{array}\right.}\)
平行なベクトルの内積
\(2\) つのベクトルが平行な場合、内積は次のように計算できます。
\(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\) のとき、
\begin{align}\color{red}{\vec{a} \ // \ \vec{b} \iff \vec{a} \cdot \vec{b} = \pm |\vec{a}||\vec{b}|}\end{align}
もちろんこれは、平面・空間ベクトルのどちらでも成り立ちます。
\(2\) つのベクトルが平行でさえあればいいので、お互いに逆向きでも問題ありません。
つまり、両者のなす角度は \(\theta = 0^\circ\) または \(180^\circ\) なので、
\(\cos \theta = \cos 0^\circ\) または \(\cos 180^\circ\)
すなわち \(\cos \theta = 1\) または \(−1\)
よって
\(\begin{align}\vec{a} \cdot \vec{b} &= |\vec{a}||\vec{b}| \cos \theta \\&= |\vec{a}||\vec{b}| \cdot (\pm 1) \\&= \color{red}{\pm |\vec{a}||\vec{b}|}\end{align}\)
と計算できますね。
ベクトルの垂直条件「内積 \(\vec{a} \cdot \vec{b} = 0\)」
\(2\) つのベクトルが垂直であるための条件を「ベクトルの垂直条件」といいます。
\(2\) つのベクトルが垂直であれば、内積は必ず \(0\) となります。
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a}\), \(\vec{b}\) に対して、
\begin{align}\vec{a} \perp \vec{b} \iff \vec{a} \cdot \vec{b} = 0\end{align}
ベクトルの垂直条件は、内積の定義から求められます。
ベクトルの内積
\(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\) のとき、\(\vec{a}\), \(\vec{b}\) のなす角を \(\theta\) \((0^\circ \leq \theta \leq 180^\circ)\) とすると、
\begin{align}\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta\end{align}
\(\vec{a}\) と \(\vec{b}\) が垂直、すなわち \(2\) つのベクトルのなす角が \(90^\circ\) なので、
\(\cos 90^\circ = 0\) より、このときの内積は
\(\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}| \cos 90^\circ = \color{red}{0}\)
この条件は問題を解く上で重要なヒントになるので、必ず覚えておきましょう。
垂直条件は平面ベクトルであろうと空間ベクトルであろうと共通ですが、成分表示では式が異なります。
平面ベクトルの垂直条件
平面ベクトル(二次元)における垂直条件は、次のように表せます。
\(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\)(ただし \(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\))のとき、
\begin{align}\vec{a} \perp \vec{b} &\iff \vec{a} \cdot \vec{b} = 0 \\&\iff \color{red}{a_1b_1 + a_2b_2 = 0 \ (成分表示)}\end{align}
これは、内積を成分表示しただけですね。
内積の成分表示については次の記事で説明しています。
 ベクトルの内積とは?公式や求め方をわかりやすく解説!
ベクトルの内積とは?公式や求め方をわかりやすく解説!
空間ベクトルの垂直条件
空間ベクトル(三次元)における垂直条件は、次のように表せます。
\(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\)(ただし \(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\))のとき、
\begin{align}\vec{a} \perp \vec{b} &\iff \vec{a} \cdot \vec{b} = 0 \\&\iff \color{red}{a_1 b_1 + a_2 b_2 + a_3 b_3 = 0 \ (成分表示)}\end{align}
(見切れる場合は横へスクロール)
こちらも、空間ベクトルの内積を成分表示しただけです。
平行条件と垂直条件の計算問題
ベクトルの平行条件や垂直条件を使った問題の解き方を説明します。
計算問題①「2 ベクトルが平行となる x の値」
\(\vec{a} = (2, x)\) と \(\vec{b} = (−3, 6)\) が平行となるように \(x\) の値を定めよ。

ベクトルが成分表示されているときは、次の \(2\) 通りの解き方ができます。
- 平行条件 \(\vec{a} = k\vec{b}\) を利用
- 成分表示の平行条件 \(a_1b_2 − a_2b_1 = 0\) を利用
\(1\) つ目は、文字 \(k\) を宣言して平行条件 \(\vec{a} = k\vec{b}\) を解く方法です。
\(\vec{a}\) と \(\vec{b}\) が平行となるとき、\(\vec{a} = k\vec{b}\) となる実数 \(k\) がある。
\((2, x) = k(−3, 6) = (−3k, 6k)\)
より、
\(\left\{\begin{array}{l} 2 = −3k …①\\ x = 6k …②\end{array}\right.\)
①より \(\displaystyle k = −\frac{2}{3}\)
②より \(x = 6 \left( − \displaystyle \frac{2}{3} \right) = −4\)
答え: \(\color{red}{x = −4}\)
\(2\) つ目は、成分表示の平行条件 \(a_1b_2 − a_2b_1 = 0\) を利用する方法です。
\(\vec{a} = (2, x)\) と \(\vec{b} = (−3, 6)\) が平行となるとき、ベクトルの平行条件より
\(2 \cdot 6 − x \cdot (−3) = 0\)
\(12 + 3x = 0\)
よって \(x = −4\)
答え: \(\color{red}{x = −4}\)
計算問題②「\(\vec{a}\) に垂直な単位ベクトルの成分」
\(\vec{a} = (2, −1)\) に垂直な単位ベクトル \(\vec{b}\) を成分で表せ。

単位ベクトル
長さが \(1\) であるベクトル。
\(\vec{b} = (x, y)\) とおいたとき、「\(\vec{b}\) の長さが \(1\) であること」と「\(\vec{a}\) と \(\vec{b}\) が垂直であること」から、\(2\) つの関係式が得られます。
\(\vec{b} = (x, y)\) とする。
\(|\vec{b}| = 1\) より
\(x^2 + y^2 = 1\) …①
ベクトルの垂直条件より、
\(\vec{a} \perp \vec{b}\) ならば \(\vec{a} \cdot \vec{b} = 0\)
\(\vec{a} = (2, −1)\)、\(\vec{b} = (x, y)\) より
\(2x + (−1)y = 0\)
\(2x − y = 0\)
\(y = 2x\) …②
②を①に代入して
\(x^2 + (2x)^2 = 1\)
\(5x^2 = 1\)
\(\displaystyle x^2 = \frac{1}{5}\)
\(\displaystyle x = \pm \frac{1}{\sqrt{5}}\)
\(\displaystyle x = \frac{1}{\sqrt{5}}\) のとき、②より \(\displaystyle y = \frac{2}{\sqrt{5}}\)
\(\displaystyle x = −\frac{1}{\sqrt{5}}\) のとき、②より \(\displaystyle y = −\frac{2}{\sqrt{5}}\)
よって、
\(\displaystyle \vec{b} = \left( \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right)\), \(\displaystyle \left( −\frac{1}{\sqrt{5}}, −\frac{2}{\sqrt{5}} \right)\)
答え:
\(\color{red}{\displaystyle \vec{b} = \left( \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right), \displaystyle \left( −\frac{1}{\sqrt{5}}, −\frac{2}{\sqrt{5}} \right)}\)
平行条件と垂直条件の証明問題
ベクトルの平行条件や垂直条件を利用する証明問題にもチャレンジしてみましょう。
証明問題①「中点連結定理を示す」
\(\triangle \mathrm{ABC}\) の \(2\) 辺 \(\mathrm{AB}\), \(\mathrm{AC}\) の中点をそれぞれ \(\mathrm{M}\), \(\mathrm{N}\) とする。
このとき、\(\mathrm{MN} \ // \ \mathrm{BC}\) であることと、\(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) であることを、ベクトルを用いて証明せよ。

まずは、ベクトルの平行条件から「\(\mathrm{MN} \ // \ \mathrm{BC} \iff \) \( \overrightarrow{\mathrm{MN}} = k \overrightarrow{\mathrm{BC}}\) となる実数 \(k\) があること」がいえます。
また、\(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\) を示すには、上記の \(k\) が \(\displaystyle \frac{1}{2}\) であることを示せばよいですね。
したがって、\(\displaystyle \overrightarrow{\mathrm{MN}} = \frac{1}{2} \overrightarrow{\mathrm{BC}}\) を示せば証明終了です。
\(\displaystyle \overrightarrow{\mathrm{MN}} = \frac{1}{2} \overrightarrow{\mathrm{BC}}\) …(*) を示せばよい。
\(\vec{b} = \overrightarrow{\mathrm{AB}}\), \(\vec{c} = \overrightarrow{\mathrm{AC}}\) とおく。
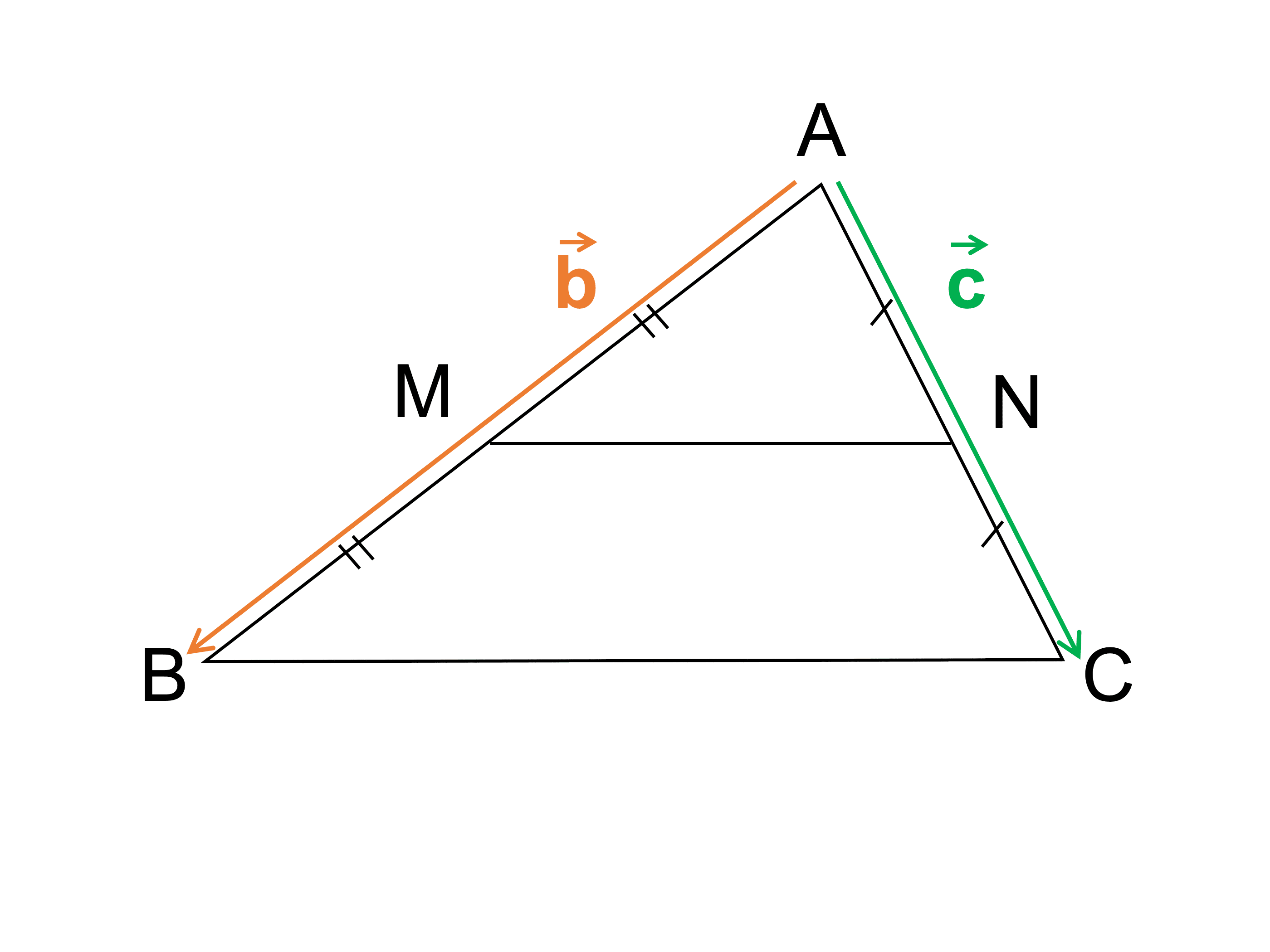
点 \(\mathrm{M}\) と点 \(\mathrm{N}\) はそれぞれ \(\mathrm{AB}\), \(\mathrm{AC}\) の中点なので、
\(\displaystyle \overrightarrow{\mathrm{AM}} = \frac{1}{2} \vec{b}\)
\(\displaystyle \overrightarrow{\mathrm{AN}} = \frac{1}{2} \vec{c}\)
(*) の両辺を \(\vec{b}\), \(\vec{c}\) を用いて表すと
\(\begin{align} \text{(左辺)} &= \overrightarrow{\mathrm{AN}} − \overrightarrow{\mathrm{AM}} \\ &= \frac{1}{2} \vec{c} − \frac{1}{2} \vec{b} \end{align}\)
\(\begin{align}\text{(右辺)} &= \frac{1}{2} (\overrightarrow{\mathrm{AC}} − \overrightarrow{\mathrm{AB}}) \\ &= \frac{1}{2} \vec{c} − \frac{1}{2}\vec{b} \end{align}\)
よって、(*) が成り立つ。
したがって、
\(\mathrm{MN} \ // \ \mathrm{BC}\) \(\) かつ \(\displaystyle \mathrm{MN} = \frac{1}{2} \mathrm{BC}\)
が示された。
(証明終わり)
証明問題②「平行四辺形とひし形の対角線」
\(4\) 本の辺の長さがすべて等しい平行四辺形をひし形という。
ひし形 \(\mathrm{ABCD}\) の \(2\) つの対角線が互いに垂直に交わることを、ベクトルを用いて証明せよ。

ベクトルの垂直条件を使って証明します。
対角線が垂直に交わることを示すので、\(2\) つの対角線をベクトルとみて、内積が \(0\) になることを示せばよいですね。
\(\overrightarrow{\mathrm{AB}} = \vec{b}\), \(\overrightarrow{\mathrm{AD}} = \vec{d}\) とおく。
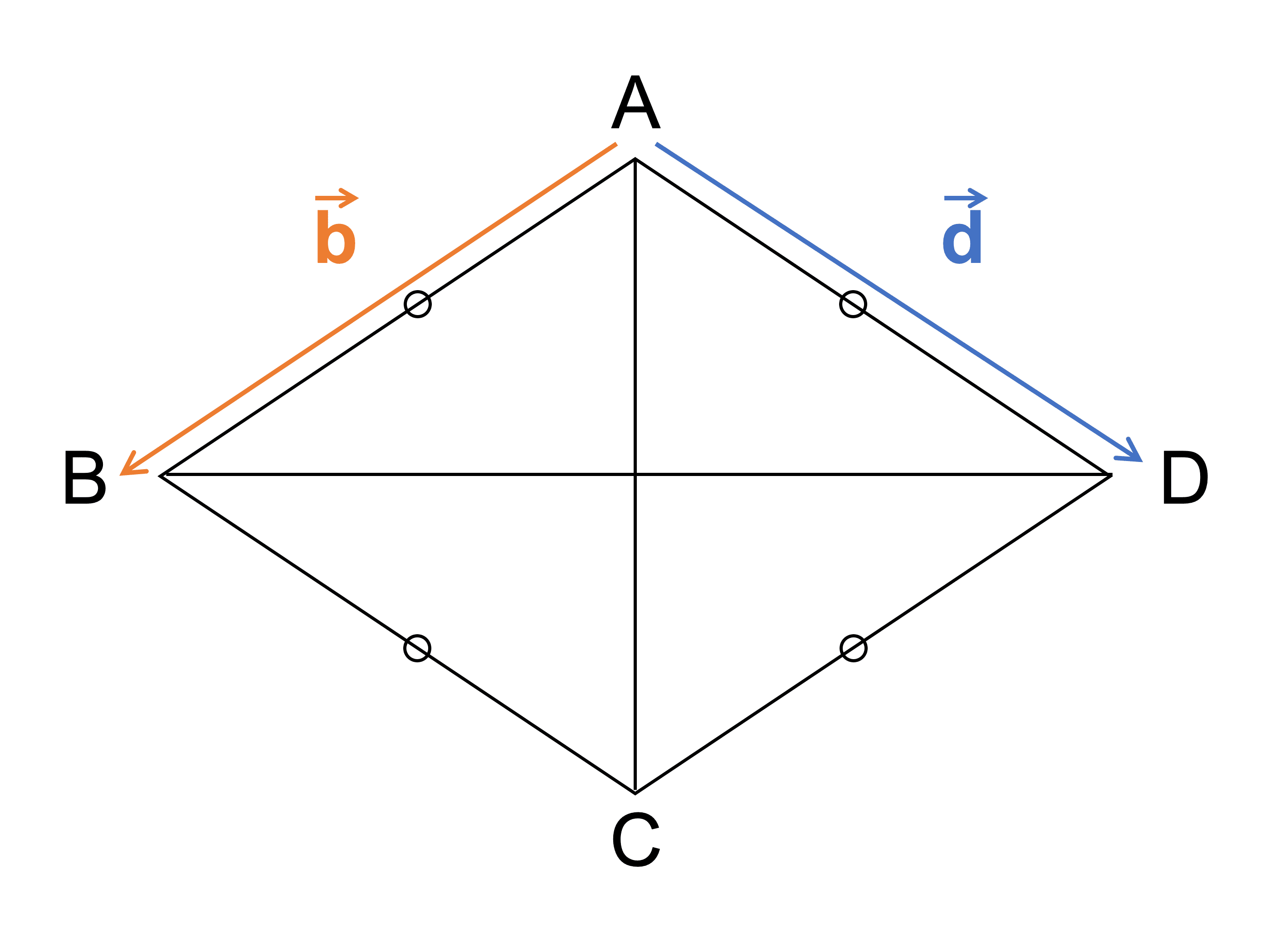
四角形 \(\mathrm{ABCD}\) は平行四辺形であるから、
\(\overrightarrow{\mathrm{BC}} = \vec{d}\), \(\overrightarrow{\mathrm{DC}} = \vec{b}\)
である。
よって
\(\overrightarrow{\mathrm{AC}} = \overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{BC}} = \vec{b} + \vec{d}\)
\(\overrightarrow{\mathrm{BD}} = \overrightarrow{\mathrm{BA}} + \overrightarrow{\mathrm{AD}} = −\vec{b} + \vec{d}\)
ここで、
\(\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BD}}\)
\(= (\vec{b} + \vec{d}) \cdot (−\vec{b} + \vec{d})\)
\(= −|\vec{b}|^2 + |\vec{d}|^2\)
四角形 \(\mathrm{ABCD}\) はひし形なので、\(|\vec{b}| = |\vec{d}|\) であるから、
\(−|\vec{b}|^2 + |\vec{d}|^2 = 0\)
すなわち
\(\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BD}} = 0\)
よって、\(\mathrm{AC} \perp \mathrm{BD}\)
ゆえに、ひし形 \(\mathrm{ABCD}\) の \(2\) つの対角線は互いに垂直に交わる。
(証明終わり)
以上で、問題も終わりです!
ベクトルの問題では、平行条件や垂直条件を使う場面がたくさんあります。
平行条件や垂直条件に慣れて、自由自在に使えるようになりましょう!
ベクトルに関するほかの公式や問題について調べたい方は、以下のまとめ記事から探してみてくださいね!
 ベクトルを総まとめ!高校で習う公式一覧
ベクトルを総まとめ!高校で習う公式一覧



