この記事では、「ベクトルの内積」の意味や公式をできるだけわかりやすく解説していきます。
内積の求め方や性質、計算問題も説明していきますので、この記事を通してぜひマスターしてくださいね。
目次
ベクトルの内積とは?
内積とは、\(2\) つのベクトル同士の向きをそろえてかけ算したものです。
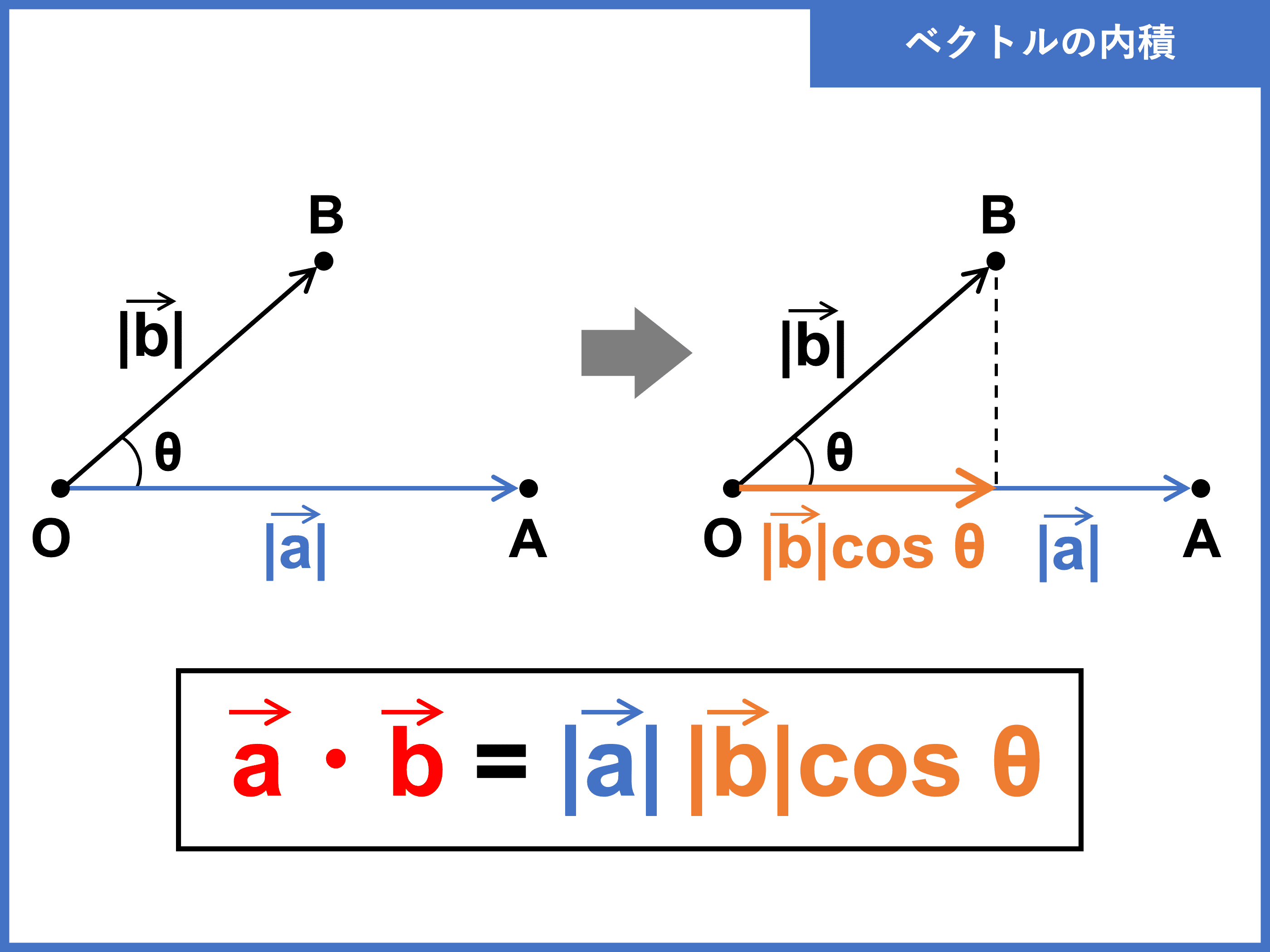
ベクトルは「大きさ」と「向き」をもつものなので、向きの異なるベクトル同士を純粋にかけ算できません。
そこで、三角比 \(\cos\theta\) を用いてベクトルの向きをそろえ、内積として定義したのです。
\(|\vec{a}|\) はベクトル \(\vec{a}\) の「大きさ」です。
\(\vec{a} = (x, y)\) のとき、 \(\vec{a}\) の大きさは三平方の定理より
\begin{align}|\vec{a}| = \sqrt{x^2 + y^2}\end{align}
と計算できます。
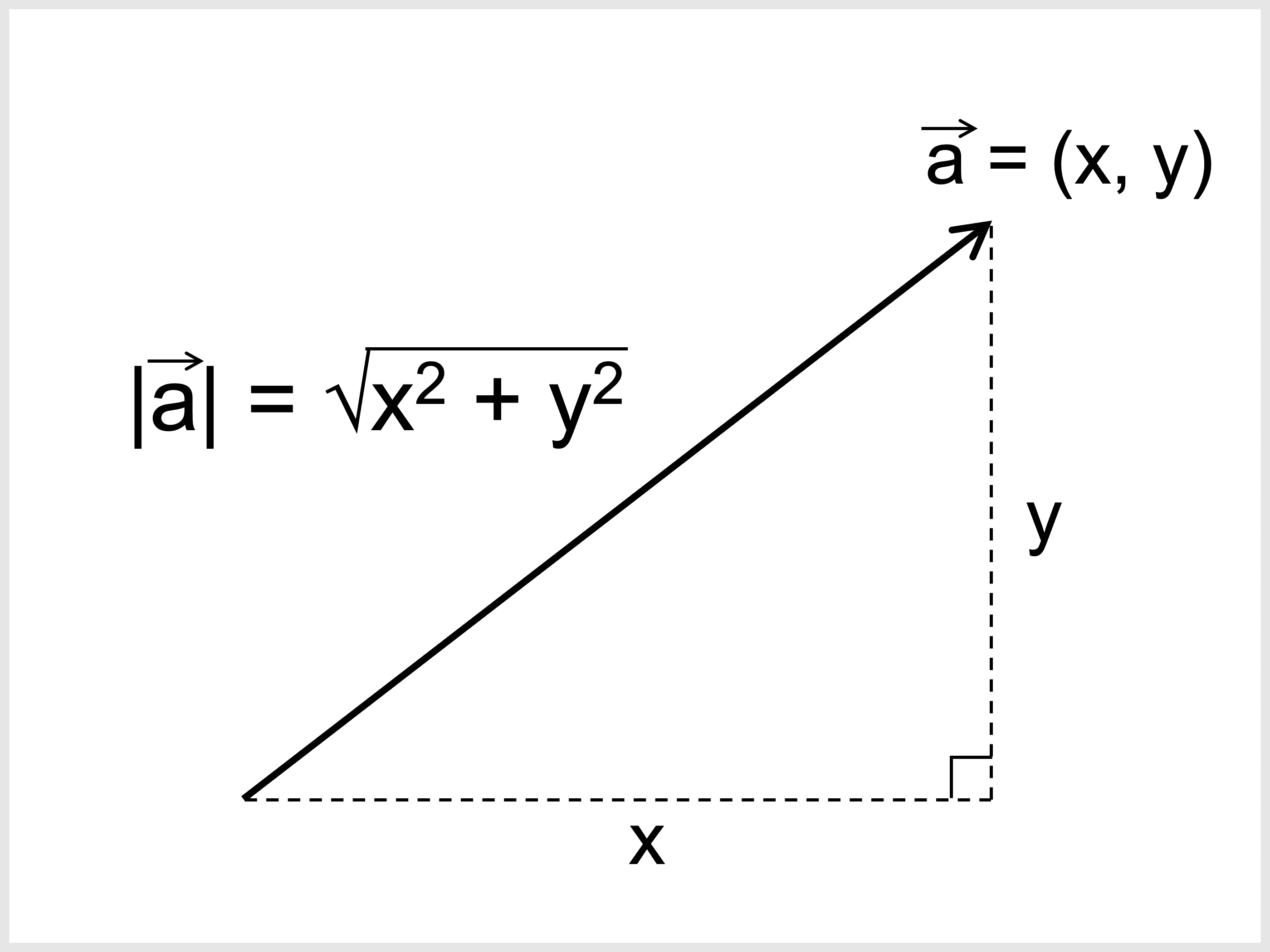
ベクトルの内積の公式
ベクトルの内積に関わる公式を示します。
公式① 内積のベクトル表示(定義)
内積の定義は、そのままベクトル表示の公式として覚えましょう。
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a}\), \(\vec{b}\) に対して、\(\vec{a}\), \(\vec{b}\) のなす角を \(\theta\) \((0^\circ \leq \theta \leq 180^\circ)\) とすると、\(\vec{a}\), \(\vec{b}\) の内積は次のように定義される。
\begin{align}\color{red}{\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta}\end{align}
なお、\(\vec{a} = \vec{0}\) または \(\vec{b} = \vec{0}\) のときは
\begin{align}\vec{a} \cdot \vec{b} = 0\end{align}
内積を求めるときは、\(2\) つのベクトルの始点をそろえるのが暗黙のルールです。
始点をそろえないと、\(2\) つのベクトルのなす角 \(\theta\) が定義できないためです。
ですので、図形問題で内積を計算する際は、始点がそろっているかを必ず確認しましょう。

公式② 内積の成分表示
\(2\) つのベクトルが成分表示されている場合、内積は次のように求められます。
\(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\) のとき
\begin{align}\color{red}{\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2}\end{align}
ベクトルが成分で表されている場合は、\(x\) 成分同士、\(y\) 成分同士の積を足し算すれば内積を求められるということですね。
なぜこの公式が成り立つのかは、余弦定理を使えば簡単に確かめられます。
余弦定理
\(\triangle \mathrm{ABC}\) について、
\begin{align}a^2 = b^2 + c^2 − 2bc \cos \mathrm{A}\end{align}
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\) の始点を合わせて点 \(\mathrm{O}\) とし、\(\vec{\mathrm{OA}} = \vec{a}\), \(\vec{\mathrm{OB}} = \vec{b}\) となるように点 \(\mathrm{A}, \mathrm{B}\) をとる。
また、\(\angle \mathrm{AOB} = \theta\) とおく。
\(\triangle \mathrm{OAB}\) について、余弦定理より
\(\mathrm{AB^2} = \mathrm{OA^2} + \mathrm{OB^2} − 2 \mathrm{OA} \cdot \mathrm{OB} \cos \theta\)
ここで、\(\mathrm{AB^2} = |\vec{b} − \vec{a}|\), \(\mathrm{OA} = |\vec{a}|\), \(\mathrm{OB} = |\vec{b}|\) より
\(|\vec{b} − \vec{a}|^2 = |\vec{a}|^2 + |\vec{b}|^2 − 2 |\vec{a}| |\vec{b}| \cos \theta\)
移項して
\(|\vec{a}| |\vec{b}| \cos \theta = \displaystyle \frac{1}{2} (|\vec{a}|^2 + |\vec{b}|^2 − |\vec{b} − \vec{a}|^2)\) …(*)
(*)の右辺を成分表示して展開・整理すると
\(\displaystyle \frac{1}{2} (|\vec{a}|^2 + |\vec{b}|^2 − |\vec{b} − \vec{a}|^2)\)
\(= \displaystyle \frac{1}{2} [(a_1^2 + a_2^2) + (b_1^2 + b_2^2) − \{(b_1 − a_1)^2 + (b_2 − a_2)^2\}]\)
\(= \displaystyle \frac{1}{2} \{a_1^2 + a_2^2 + b_1^2 + b_2^2 − (b_1^2 − 2a_1b_1 + a_1^2 + b_2^2 − 2a_2b_2 + a_2^2)\}\)
\(= \displaystyle \frac{1}{2} (a_1^2 + a_2^2 + b_1^2 + b_2^2 − b_1^2 + 2a_1b_1 − a_1^2 − b_2^2 + 2a_2b_2 − a_2^2)\)
\(= \displaystyle \frac{1}{2} (2a_1b_1 + 2a_2b_2)\)
\(= \displaystyle \frac{1}{2} \cdot 2(a_1b_1 + a_2b_2)\)
\(= a_1b_1 + a_2b_2\)
(見切れる場合は横へスクロール)
ここで、(*)の左辺は内積 \(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta\) であるから、
\(\color{red}{\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2}\)
が成り立つ。
(証明終わり)
公式③ ベクトルのなす角
内積の公式①を \(\cos \theta\) について解くと、\(2\) つのベクトルのなす角がわかります。
\(\vec{0}\) でない \(2\) つのベクトル \(\vec{a} = (a_1, a_2)\), \(\vec{b} = (b_1, b_2)\) のなす角を \(\theta\) とすると
\begin{align}\displaystyle \cos \theta &= \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} \\&= \displaystyle \frac{a_1 b_1 + a_2 b_2}{\sqrt{a_1^2 + a_2^2} \sqrt{b_1^2 + b_2^2}}\end{align}
このように内積は角度の情報をもち合わせているので、ベクトル同士の関係性や両者がなす角を知るのにとても便利なツールなのです。
ベクトルの内積の求め方
例題を通してベクトルの内積の求め方を説明していきます。
ポイントは、与えられた情報から適切な内積の公式を選ぶことです。
例題①「ベクトルの大きさと角度から求める」
\(|\vec{a}| = 4\), \(|\vec{b}| = 3\)、\(\vec{a}\), \(\vec{b}\) のなす角 \(\theta = 45^\circ\) のとき、内積 \(\vec{a} \cdot \vec{b}\) を求めよ。
「大きさ」と「角度」が与えられているときは、ベクトル表示の公式① \(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta\) で内積を求めます。
\(\begin{align} \vec{a} \cdot \vec{b} &= |\vec{a}| |\vec{b}| \cos 45^\circ \\ &= 4 \cdot 3 \cdot \frac{\sqrt{2}}{2} \\ &= 6\sqrt{2} \end{align}\)
答え: \(\color{red}{6\sqrt{2}}\)
例題②「ベクトルの成分から求める」
\(\vec{a} = (2, 3)\), \(\vec{b} = (−5,4)\) のとき、内積 \(\vec{a} \cdot \vec{b}\) を求めよ。
ベクトルの「成分」が与えられているときは、成分表示の公式② \(\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2\) で内積を求めます。
\(\begin{align} \vec{a} \cdot \vec{b} &= a_1 b_1 + a_2 b_2 \\&= 2 \cdot (−5) + 3 \cdot 4 \\&= −10 + 12 \\ &= 2 \end{align}\)
答え: \(\color{red}{2}\)
ベクトルの内積の性質
ベクトルの内積がもつ性質を説明していきます。
性質① 内積の計算法則
内積記号「\(\cdot\)」を扱うときは、基本的にふつうのかけ算記号「\(\times\)」と同じように交換・分配・定数のくくり出しができます。
ベクトル \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) について、次が成り立つ。
- 交換法則
\begin{align}\color{red}{\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}}\end{align} - 分配法則
\begin{align}\color{red}{\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}}\end{align} - 定数倍
\begin{align}\color{red}{(k \vec{a}) \cdot \vec{b} = \vec{a} \cdot (k \vec{b}) = k (\vec{a} \cdot \vec{b})}\end{align}
性質② ベクトルの大きさと内積
ベクトルの大きさと内積には、次の関係があります。
ベクトル \(\vec{a}\), \(\vec{b}\) について、次が成り立つ。
- \(\color{red}{\vec{a} \cdot \vec{a} = |\vec{a}|^2}\)
- \(\color{red}{|\vec{a}| = \sqrt{\vec{a} \cdot \vec{a}}}\)
- \(\color{red}{−|\vec{a}| |\vec{b}| \leq \vec{a} \cdot \vec{b} \leq |\vec{a}| |\vec{b}|}\)
ポイントは、「\(\vec{a}^2\) は存在しない」ということです。
\(\vec{a}\) が \(\vec{a}\) 自身となす角は \(0^\circ\) ですから、内積の定義に当てはめると
\(\begin{align} \vec{a} \cdot \vec{a} &= |\vec{a}| |\vec{a}| \cos 0^\circ \\ &= |\vec{a}|^2 \end{align}\)
(ベクトルの大きさの \(2\) 乗)
となり、決して \(\vec{a}^2\)(ベクトルの \(2\) 乗)にはなりません。
「ベクトル(\(\vec{a}\))」「ベクトルの大きさ(\(|\vec{a}|\))」「ベクトルの内積(\(\vec{a} \cdot \vec{b}\))」の違いは明確に理解しておきましょう。
性質③ 平行・垂直なベクトルの内積
平行な \(2\) つのベクトルの内積は(\(\pm\) 大きさの積)に、垂直な \(2\) つのベクトルの内積は \(0\) になります。
\(\vec{a} \neq \vec{0}\), \(\vec{b} \neq \vec{0}\) のとき、
- 平行なベクトルの内積
\begin{align}\vec{a} \ // \ \vec{b} &\iff \vec{a} \cdot \vec{b} = \pm |\vec{a}||\vec{b}|\end{align} - 垂直なベクトルの内積
\begin{align}\vec{a} \perp \vec{b} &\iff \vec{a} \cdot \vec{b} = 0 \\&\iff a_1b_1 + a_2b_2 = 0\end{align}
これらの条件は問題を解く上で重要なヒントになるので、必ず覚えておきましょう。
\(2\) つのベクトルが平行であるとき、ベクトルの向きはどちらでもよいので、
両者のなす角度は \(\theta = 0^\circ\) または \(180^\circ\)
よって
\(\cos \theta = \cos 0^\circ\) または \(\cos 180^\circ\)
すなわち \(\cos \theta = 1\) または \(−1\)
よって
\(\begin{align}\vec{a} \cdot \vec{b} &= |\vec{a}||\vec{b}| \cos \theta \\&= |\vec{a}||\vec{b}| \cdot (\pm 1) \\&= \color{red}{\pm |\vec{a}||\vec{b}|}\end{align}\)
(証明終わり)
\(2\) つのベクトルのなす角が \(90^\circ\) のとき、
\(\begin{align}\vec{a} \cdot \vec{b} &= |\vec{a}||\vec{b}| 90^\circ \\&= |\vec{a}||\vec{b}| \cdot 0 \\&= \color{red}{0}\end{align}\)
(証明終わり)
内積以外にも、ベクトルが平行または垂直であることを示す条件がいくつかあります。
 ベクトルの平行条件、垂直条件とは?内積公式や証明問題を解説
ベクトルの平行条件、垂直条件とは?内積公式や証明問題を解説
ベクトルの内積の計算問題
ベクトルの内積がかかわる計算問題にチャレンジしてみましょう。
計算問題①「2 つのベクトルがなす角度を求める」
\(2\) つのベクトル \(\vec{a} = (−\sqrt{3}, 1)\), \(\vec{b} = (3, \sqrt{3})\) のなす角 \(\theta\) を求めよ。
ただし、\(0^\circ \leq \theta \leq 180^\circ\) とする。

\(2\) つのベクトルのなす角は公式③「\(\cos \theta = \) 〜」で求められましたね。
内積 \(\vec{a} \cdot \vec{b}\) のほかに、各ベクトルの大きさ \(|\vec{a}|\), \(|\vec{b}|\) も先に求めておくと計算がスムーズですよ!
まず、\(\vec{a} \cdot \vec{b}\), \(|\vec{a}|\), \(|\vec{b}|\) を求める。
\(\begin{align} \vec{a} \cdot \vec{b} &= (−\sqrt{3}) \cdot 3 + 1 \cdot \sqrt{3} \\&= −3\sqrt{3} + \sqrt{3} \\ &= −2\sqrt{3} \end{align}\)
\(\begin{align} |\vec{a}| &= \sqrt{(−\sqrt{3})^2 + 1^2} \\ &= \sqrt{4} \\ &= 2 \end{align}\)
\(\begin{align} |\vec{b}| &= \sqrt{3^2 + (\sqrt{3})^2} \\ &= \sqrt{12} \\ &= 2\sqrt{3} \end{align}\)
したがって、
\(\begin{align} \cos \theta &= \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} \\ &= \frac{−2\sqrt{3}}{2 \cdot 2\sqrt{3}} \\ &= −\frac{1}{2} \end{align}\)
\(0^\circ \leq \theta \leq 180^\circ\) より、\(\theta = 120^\circ\)
答え: \(\theta = 120^\circ\)
計算問題②「垂直なベクトルの成分を求める」
\(\vec{a} = (3, 5)\), \(\vec{b} = (x, 6)\) が垂直であるとき、\(x\) の値を求めよ。

ベクトルの問題で「垂直」というキーワードが出たら「内積は 0!」と瞬時に反応してください。
\(\vec{a}\) と \(\vec{b}\) は垂直なので、
\(\vec{a} \cdot \vec{b} = 0\)
\(\vec{a} \cdot \vec{b} = 3x + 30\) より、
\(3x + 30 = 0\)
\(x = −10\)
答え: \(x = −10\)
計算問題③「大きさから内積を求める」
\(|\vec{a}| = 1\), \(|\vec{b}| = 3\), \(|\vec{a} + \vec{b}| = \sqrt{6}\) のとき \(\vec{a} \cdot \vec{b}\) の値を求めよ。

\(|\vec{a} + \vec{b}| = \sqrt{6}\) を \(2\) 乗すると、\(\vec{a} \cdot \vec{b}\) に関する方程式が得られそうです。
\(|\vec{a} + \vec{b}| = \sqrt{6}\) の両辺を \(2\) 乗すると
\(|\vec{a} + \vec{b}|^2 = 6\)
\(|\vec{a}|^2 + 2\vec{a} \cdot \vec{b} + |\vec{b}|^2 = 6\)
\(|\vec{a}| = 1\), \(|\vec{b}| = 3\) より
\(1^2 + 2 \vec{a} \cdot \vec{b} + 3^2 = 6\)
\(2 \vec{a} \cdot \vec{b} + 10 = 6\)
\(2 \vec{a} \cdot \vec{b} = −4\)
\(\vec{a} \cdot \vec{b} = −2\)
答え: \(\vec{a} \cdot \vec{b} = −2\)
以上で計算問題も終わりです!
内積はベクトルの計算において大変重要です。
いろいろな問題を解きながら、ベクトルの内積に慣れていきましょう!
ベクトルに関するほかの公式や問題について調べたい方は、以下のまとめ記事から探してみてくださいね。
 ベクトルを総まとめ!高校で習う公式一覧
ベクトルを総まとめ!高校で習う公式一覧

