この記事では、「空間ベクトル」についてできるだけわかりやすく解説していきます。
空間ベクトルの内積、面積、垂直条件・平行条件といった公式や問題の解き方を説明していきますので、この記事を通してぜひマスターしてくださいね。
目次
空間ベクトルとは?
空間ベクトルとは、文字通り「空間内にあるベクトル」のことです。
平面ベクトルでは「\(x\), \(y\) 方向の二次元」を考えるのに対し、空間ベクトルでは 「\(x\), \(y\), \(z\) 方向の三次元」を考えます。
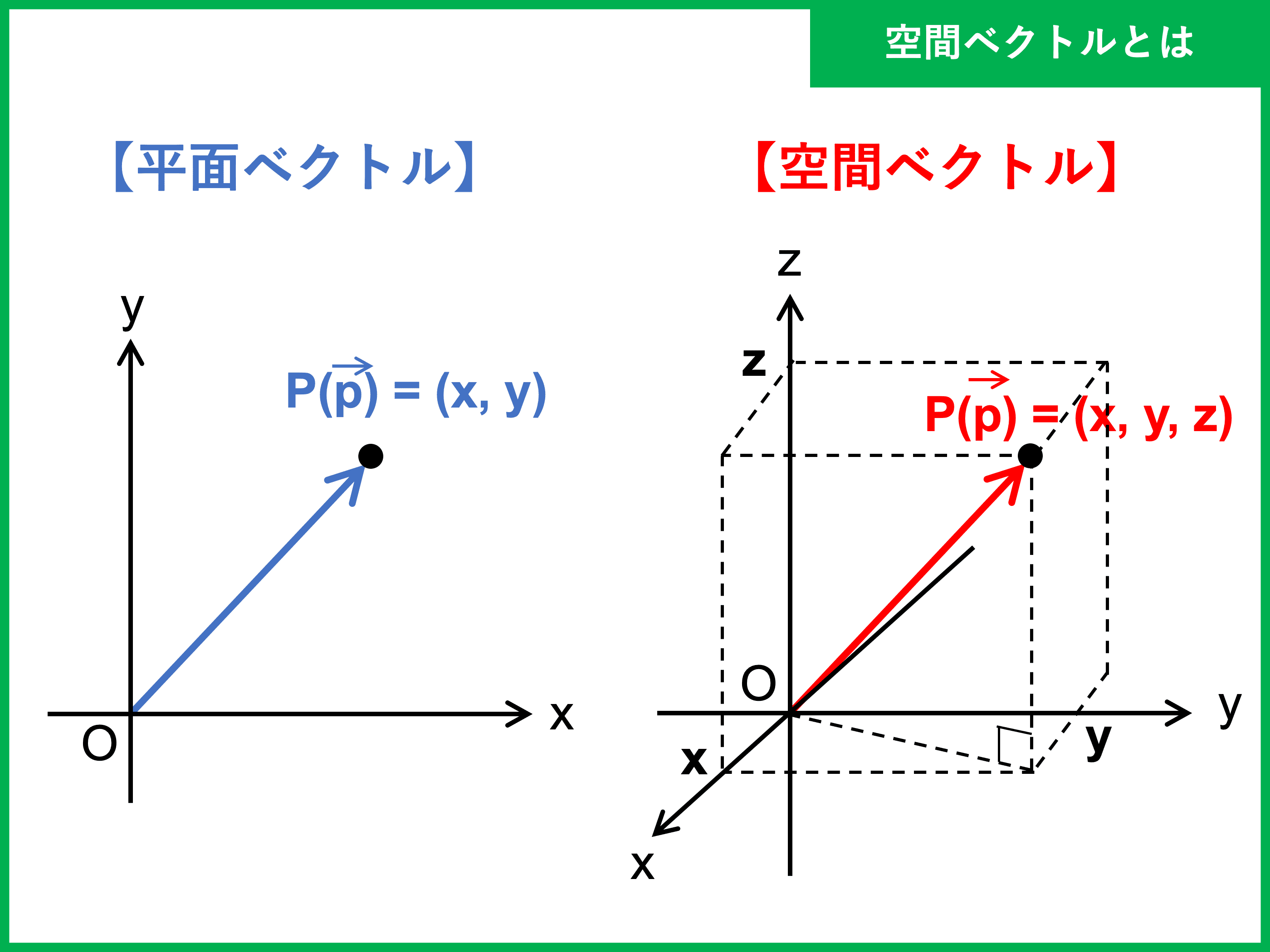
「空間」というと難しい印象があるかもしれませんが、平面のときと同じ考え方でいいのです。
以降、空間ベクトルに関する公式を紹介していきますが、新たに丸暗記するというよりは、「平面ベクトルの公式との関連性」を意識しましょう。
空間ベクトルの基本公式
空間ベクトルの基本公式を示します。
空間ベクトルの成分表示
原点を \(\mathrm{O}\) とする座標空間において、\(\vec{a} = \overrightarrow{\mathrm{OA}}\) となる点 \(\mathrm{A}(a_1, a_2, a_3)\) をとると、\(\vec{a}\) は次のように表される。
\begin{align}\vec{a} = (a_1, a_2, a_3)\end{align}
\(a_1\) を \(x\) 成分、\(a_2\) を \(y\) 成分、\(a_3\) を \(z\) 成分という。
なお、以下のまとめ記事で説明しているベクトルの計算規則は空間ベクトルでも当然成り立ちます。
空間ベクトルに関して特別に気をつけるべきなのは、成分が \(x\), \(y\), \(z\) の \(3\) 方向になることだけですね。
空間ベクトルの相等
\(2\) つの空間ベクトルが等しいということは、各成分が完全に一致するということです。
\(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\) について
\begin{align}\vec{a} = \vec{b} \iff a_1 = b_1, a_2 = b_2, a_3 = b_3\end{align}
空間ベクトルの大きさ
空間ベクトルの大きさは次のように計算できます。
- \(\vec{a}\) の大きさ
\(\vec{a} = (a_1, a_2, a_3)\) のとき、
\begin{align}\color{red}{|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}}\end{align}
- \(2\) 点を結ぶベクトルの大きさ
\(\mathrm{A}(a_1, a_2, a_3)\), \(\mathrm{B}(b_1, b_2, b_3)\) のとき、
\(\overrightarrow{\mathrm{AB}} = \overrightarrow{\mathrm{OB}} − \overrightarrow{\mathrm{OA}} = (b_1 − a_1, b_2 − a_2, b_3 − a_3)\) より
\begin{align}\color{red}{|\overrightarrow{\mathrm{AB}}| = \sqrt{(b_1 − a_1)^2 + (b_2 − a_2)^2 + (b_3 − a_3)^2}}\end{align}
(見切れる場合は横へスクロール)
座標空間における「\(2\) 点間の距離」と考え方は同じですね。
空間ベクトルの分解
平面ベクトルが平行でない \(2\) つのベクトルに分解できたように、空間ベクトルは同じ平面上にない \(3\) つのベクトルに分解できます。
同じ平面上にない \(4\) 点 \(\mathrm{O}\), \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\) に対して、\(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\), \(\overrightarrow{\mathrm{OC}} = \vec{c}\) とする。
このとき、空間内のどんなベクトル \(\vec{p}\) も、実数 \(s\), \(t\), \(u\) を用いてただ \(1\) 通りに
\begin{align}\color{red}{\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}}\end{align}
と表すことができる。

これは空間ベクトルの計算でよく使う考え方なので、しっかり把握しておきましょう。
空間ベクトルの内積の公式
空間ベクトルの内積は、ベクトル表示の場合は平面ベクトルとまったく同じ式です。
成分表示にしても \(z\) 成分が増えるだけで、「\(2\) つのベクトルの成分を、成分ごとにかけて足す」という演算は平面ベクトルと共通です。
\(\vec{0}\) でない \(2\) つの空間ベクトル \(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\) がなす角を \(\theta\) \((0^\circ \leq \theta \leq 180^\circ)\) とする。
- ベクトル表示の公式
\begin{align}\color{red}{\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta}\end{align}
- 成分表示の公式
\begin{align}\color{red}{\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3}\end{align}
- ベクトルのなす角の公式
\begin{align}\color{red}{\displaystyle \cos \theta \ } & \color{red}{= \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}} \\&\color{red}{= \displaystyle \frac{a_1 b_1 + a_2 b_2 + a_3b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2} \sqrt{b_1^2 + b_2^2 + b_3^2}}}\end{align}
(見切れる場合は横へスクロール)
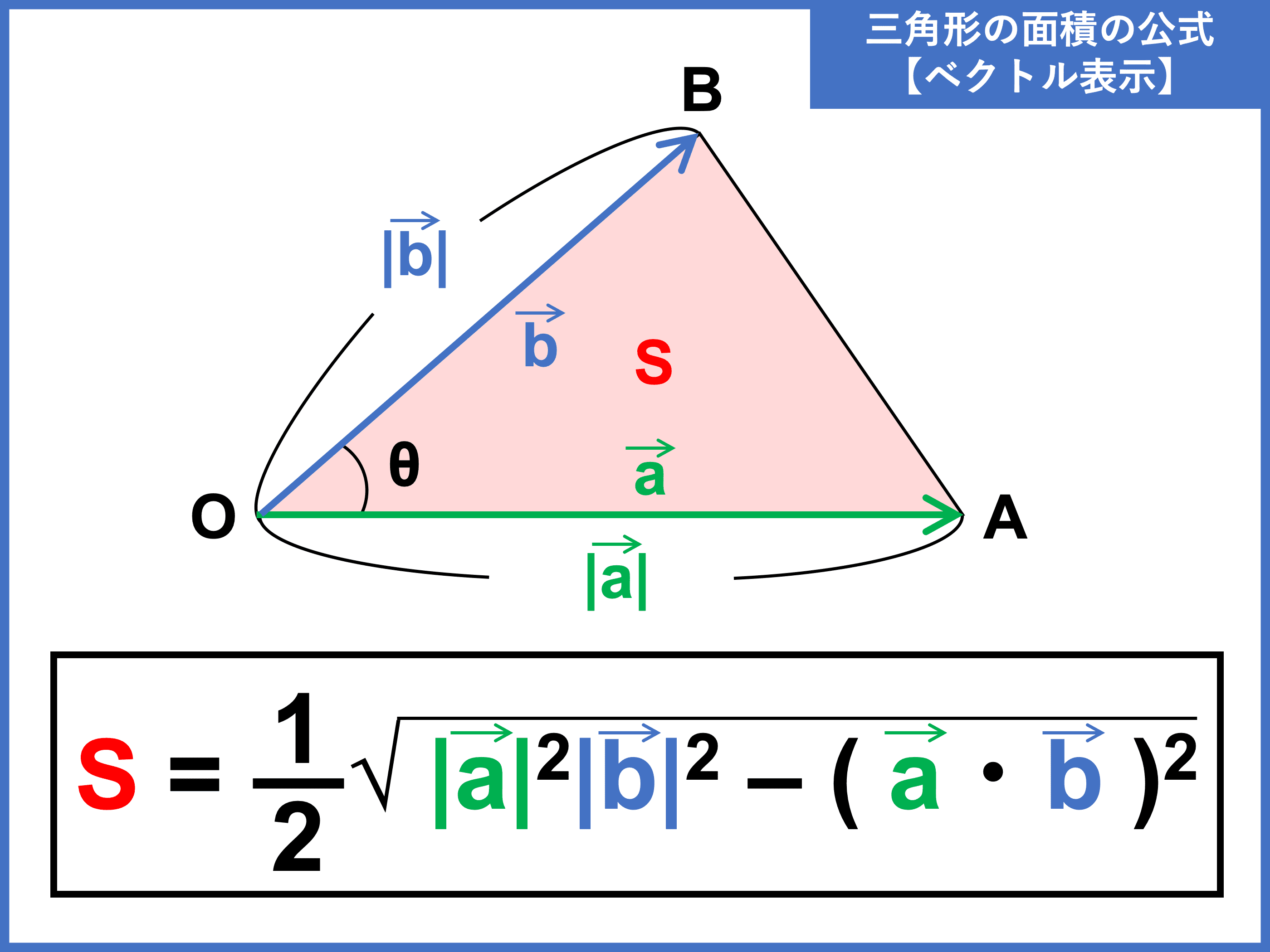
空間ベクトルと三角形の面積の公式
空間内にある三角形の面積の公式も、ベクトル表示なら平面のときとまったく同じです。
\(\triangle \mathrm{OAB}\) において、 \(\overrightarrow{\mathrm{OA}} = \vec{a}\), \(\overrightarrow{\mathrm{OB}} = \vec{b}\) とすると、 \(\triangle \mathrm{OAB}\) の面積 \(S\) は
\begin{align}\color{red}{\displaystyle S = \frac{1}{2} \sqrt{ |\vec{a}|^2 |\vec{b}|^2 − (\vec{a} \cdot \vec{b})^2 }}\end{align}
ちなみに、成分表示による三角形の面積は次のとおりですが、こちらはそれほど使わないので無理に暗記する必要はありません。
\(\mathrm{A}(\vec{a}) = (a_1, a_2, a_3)\), \(\mathrm{B}(\vec{b}) = (b_1, b_2, b_3)\) のとき、\(\triangle \mathrm{OAB}\) の面積 \(S\) は
\begin{align}\color{red}{S = \frac{1}{2} \sqrt{(a_1 b_2 − a_2 b_1)^2 + (a_2 b_3 − a_3 b_2)^2 + (a_3 b_1 − a_1 b_3)^2}}\end{align}
(見切れる場合は横へスクロール)
考え方は平面ベクトルのときと同じなものの、少し複雑になりますね。
空間ベクトルの平行条件と垂直条件
空間ベクトルの平行条件と垂直条件も、平面ベクトルの場合とまったく同じです。
成分表示のときの計算に注意しましょう。
\(\vec{0}\) でない \(2\) つの空間ベクトル \(\vec{a} = (a_1, a_2, a_3)\), \(\vec{b} = (b_1, b_2, b_3)\) において、
- 空間ベクトルの平行条件
\begin{align}\vec{a} \ // \ \vec{b} &\iff \vec{a} = k \vec{b} \ \text{となる実数} \ k \ \text{がある} \\ &\iff \left\{\begin{array}{l} a_1 b_2 − a_2 b_1 = 0 \\ a_2b_3 − a_3b_2 = 0 \\ a_3b_1 − a_1b_3 = 0 \end{array}\right. \ \text{(成分表示)}\end{align} - 空間ベクトルの垂直条件
\begin{align}\vec{a} \perp \vec{b} & \iff \vec{a} \cdot \vec{b} = 0 \\& \iff a_1 b_1 + a_2 b_2 + a_3 b_3 = 0 \ \text{(成分表示)}\end{align}
(見切れる場合は横へスクロール)
空間ベクトルの位置ベクトル
空間ベクトルの位置ベクトルの公式についても平面ベクトルと共通であり、成分表示で \(z\) 成分が増えるだけです。
(見切れる場合は横へスクロール)
- 内分点の位置ベクトル
線分 \(\mathrm{AB}\) を \(m : n\) に内分する点 \(\mathrm{P}\) の位置ベクトル \(\vec{p}\) は
\begin{align}\vec{p} &= \frac{n \vec{a} + m \vec{b}}{m + n} \\&= \left(\frac{n a_1 + m b_1}{m + n}, \frac{n a_2 + m b_2}{m + n}, \frac{n a_3 + m b_3}{m + n}\right) \end{align}
- 外分点の位置ベクトル
線分 \(\mathrm{AB}\) を \(m : n\) に外分する点 \(\mathrm{Q}\) の位置ベクトル \(\vec{q}\) は
\begin{align}\vec{q} &= \frac{−n \vec{a} + m \vec{b}}{m − n} \\&= \left(\frac{−n a_1 + m b_1}{m − n}, \frac{−n a_2 + m b_2}{m − n}, \frac{−n a_3 + m b_3}{m − n}\right) \end{align}
- 三角形の重心の位置ベクトル
\(3\) 点 \(\mathrm{A}(\vec{a}) = (a_1, a_2, a_3)\), \(\mathrm{B}(\vec{b}) = (b_1, b_2, b_3)\), \(\mathrm{C}(\vec{c}) = (c_1, c_2, c_3)\) を頂点とする \(\triangle \mathrm{ABC}\) の重心 \(\mathrm{G}\) の位置ベクトル \(\vec{g}\) は
\begin{align}\displaystyle \vec{g} &= \frac{\vec{a} + \vec{b} + \vec{c}}{3} \\&= \left(\frac{a_1 + b_1 + c_1}{3}, \frac{a_2 + b_2 + c_2}{3}, \frac{a_3 + b_3 + c_3}{3}\right)\end{align}
空間ベクトルのベクトル方程式
ベクトル方程式のほとんどは、平面ベクトルと共通です(直線、円、平面の方程式など)。
成分や座標を計算するときだけ、\(x, y, z\) 方向すべてを考えるようにします。
空間特有のベクトル方程式は、「空間における平面のベクトル方程式」「球面のベクトル方程式」「空間ベクトルの共面条件」などです。詳しくは以下の記事で説明しています。
空間ベクトルの問題の解き方
空間ベクトルの計算問題の解き方を説明します。
計算問題①「空間ベクトルの成分と分解」
\(3\) つのベクトル \(\vec{a} = (1, 2, 3)\), \(\vec{b} = (2, 5, 4)\), \(\vec{c} = (−2, 0, −1)\) が同一平面上にないとき、\(\vec{p} = (−3, 7, 4)\) を \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) を用いて表せ。

空間ベクトルは、同じ平面上にない \(3\) つのベクトルに分解できるのでしたね。
任意の定数を使って \(\vec{p}\) を \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) で表し、成分に関する連立方程式を解きましょう。
(見切れる場合は横へスクロール)
\(\vec{a}\), \(\vec{b}\), \(\vec{c}\) は同一平面上にないので、
\(\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}\) とおける。
\(\vec{a} = (1, 2, 3)\), \(\vec{b} = (2, 5, 4)\), \(\vec{c} = (−2, 0, −1)\) より、
\(\begin{align}\vec{p} &= (sa_1 + tb_1 + uc_1, sa_2 + tb_2 + uc_2, sa_3 + tb_3 + uc_3) \\&= (s \cdot 1 + t \cdot 2 + u \cdot (−2), s \cdot 2 + t \cdot 5 + u \cdot 0, s \cdot 3 + t \cdot 4 + u \cdot (−1))\\&= (s + 2t − 2u, 2s + 5t, 3s + 4t − u) \end{align}\)
これが \((−3, 7, 4)\) に等しいから、
\(\left\{\begin{array}{l} s + 2t − 2u = −3 \cdots ①\\ 2s + 5t = 7 \cdots ②\\ 3s + 4t − u = 4 \cdots ③\end{array}\right.\)
\(② − ① \times 2\) より
\(\begin{array}{rr} 2s + 5t =& 7 \color{white}{ \ }\\ −) 2s + 4t − 4u =& −6 \color{white}{ \ }\\ \hline t + 4u =& 13 \cdots ④ \end{array}\)
\(① \times 3 − ③\) より
\(\begin{array}{rr} 3s + 6t − 6u =& −9 \color{white}{ \ }\\ −) 3s + 4t − u =& 4 \color{white}{ \ }\\ \hline 2t − 5u =& −13 \cdots ⑤ \end{array}\)
\(④ \times 2 − ⑤\) より
\(\begin{array}{rr} 2t + 8u =& 26\\ −) 2t − 5u =& −13\\ \hline 13u =& 39 \end{array}\)
よって \(u = 3\)
\(④\) より
\(\begin{align}t &= 13 − 4u \\&= 13 − 4 \cdot 3 \\&= 13 − 12 \\&= 1\end{align}\)
\(①\) より
\(\begin{align}s &= −3 − 2t + 2u \\&= −3 − 2 \cdot 1 + 2 \cdot 3 \\&= −3 − 2 + 6 \\&= 1\end{align}\)
したがって、
\(\begin{align}\vec{p} &= s\vec{a} + t\vec{b} + u\vec{c} \\&= \vec{a} + \vec{b} + 3\vec{c}\end{align}\)
答え: \(\color{red}{\vec{p} = \vec{a} + \vec{b} + 3\vec{c}}\)
計算問題②「空間ベクトルがなす角」
\(2\) つのベクトル \(\vec{a} = (1, x, 0)\), \(\vec{b} = (x + 1, 0, x − 1)\) のなす角が \(45^\circ\) となるように \(x\) の値を定めよ。

\(2\) つのベクトルがなす角を求めるには、その内積を利用すればよいですね。
さきに各ベクトルの大きさ \(|\vec{a}|\), \(|\vec{b}|\) と内積 \(\vec{a} \cdot \vec{b}\) を成分で表しておくとスムーズです。
\(\begin{align} |\vec{a}| &= \sqrt{1^2 + x^2 + 0^2} \\ &= \sqrt{x^2 + 1} \end{align}\)
\(\begin{align} |\vec{b}| &= \sqrt{(x + 1)^2 + 0^2 + (x − 1)^2} \\ &= \sqrt{2x^2 + 2} \\ &= \sqrt{2} \sqrt{x^2 + 1} \end{align}\)
\(\begin{align} \vec{a} \cdot \vec{b} &= 1 \cdot (x + 1) + x \cdot 0 + 0 \cdot (x − 1) \\ &= x + 1 \end{align}\)
\(\vec{a}\) と \(\vec{b}\) のなす角が \(45^\circ\) になればよいので、
\(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos 45^\circ\)
よって
\(\displaystyle x + 1 = \sqrt{x^2 + 1} \cdot \sqrt{2} \sqrt{x^2 + 1} \cdot \frac{1}{\sqrt{2}}\)
\(x + 1 = x^2 + 1\)
\(x^2 + 1 = x + 1\)
\(x^2 − x = 0\)
\(x(x − 1) = 0\)
\(x = 0, 1\)
答え: \(\color{red}{x = 0, 1}\)
計算問題③「空間ベクトルと三角形の面積」
\(3\) 点 \(\mathrm{A}(1, 1, 4)\), \(\mathrm{B}(2, 1, 5)\), \(\mathrm{C}(3, −1, 8)\) を頂点とする \(\triangle \mathrm{ABC}\) の面積を求めよ。

三角形の面積を求める公式 \(\displaystyle S = \frac{1}{2} \sqrt{|\overrightarrow{\mathrm{AB}}|^2 |\overrightarrow{\mathrm{AC}}|^2 − (\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}})^2}\) を使います。
さきに \(\overrightarrow{\mathrm{AB}}\) と \(\overrightarrow{\mathrm{AC}}\) の大きさおよび内積を成分から計算しておきましょう。
\(\begin{align}\overrightarrow{\mathrm{AB}} &= \overrightarrow{\mathrm{OB}} − \overrightarrow{\mathrm{OA}} \\&= (2 − 1, 1 − 1, 5 − 4) \\&= (1, 0, 1)\end{align}\)
\(\begin{align}\overrightarrow{\mathrm{AC}} &= \overrightarrow{\mathrm{OC}} − \overrightarrow{\mathrm{OA}} \\&= (3 − 1, −1 − 1, 8 − 4) \\&= (2, −2, 4)\end{align}\)
であるから、
\(|\overrightarrow{\mathrm{AB}}| = \sqrt{1^2 + 0^2 + 1^2} = \sqrt{2}\)
\(|\overrightarrow{\mathrm{AC}}| = \sqrt{2^2 + (−2)^2 + 4^2} = \sqrt{24}\)
\(\begin{align} \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}} &= 1 \cdot 2 + 0 \cdot (−2) + 1 \cdot 4 \\ &= 6 \end{align}\)
\(\triangle \mathrm{ABC}\) の面積を \(S\) とすると
\(\begin{align} S &= \frac{1}{2} \sqrt{|\overrightarrow{\mathrm{AB}}|^2 |\overrightarrow{\mathrm{AC}}|^2 − (\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}})^2} \\ &= \frac{1}{2} \sqrt{2 \cdot 24 − 6^2} \\ &= \frac{1}{2} \sqrt{48 − 36} \\ &= \frac{1}{2} \sqrt{12} \\ &= \frac{1}{2} \cdot 2\sqrt{3} \\ &= \sqrt{3} \end{align}\)
答え: \(\color{red}{\sqrt{3}}\)
ちなみに、成分表示の公式を使っても求められます。
(見切れる場合は横へスクロール)
\(\begin{align}\overrightarrow{\mathrm{AB}} &= \overrightarrow{\mathrm{OB}} − \overrightarrow{\mathrm{OA}} \\&= (2 − 1, 1 − 1, 5 − 4) \\&= (1, 0, 1) \\&= (b_1, b_2, b_3)\end{align}\)
\(\begin{align}\overrightarrow{\mathrm{AC}} &= \overrightarrow{\mathrm{OC}} − \overrightarrow{\mathrm{OA}} \\&= (3 − 1, −1 − 1, 8 − 4) \\&= (2, −2, 4) \\&= (c_1, c_2, c_3)\end{align}\)
とするとき、
\(\triangle \mathrm{ABC}\) の面積 \(S\) は
\(\begin{align}S &= \frac{1}{2} \sqrt{(b_1 c_2 − b_2 c_1)^2 + (b_2 c_3 − b_3 c_2)^2 + (b_3 c_1 − b_1 c_3)^2} \\&= \frac{1}{2} \sqrt{\{1 \cdot (−2) − 0 \cdot 2\}^2 + \{0 \cdot 4 − 1 \cdot (−2)\}^2 + (1 \cdot 2 − 1 \cdot 4)^2} \\&= \frac{1}{2} \sqrt{(−2)^2 + 2^2 + (−2)^2} \\&= \frac{1}{2} \sqrt{4 + 4 + 4} \\&= \frac{1}{2} \sqrt{12} \\&= \frac{1}{2} \cdot 2\sqrt{3} \\&= \sqrt{3}\end{align}\)
答え: \(\color{red}{\sqrt{3}}\)
計算問題④「空間ベクトルと二次関数」
\(\vec{a} = (1, 1, −1)\), \(\vec{b} = (2, −1, −1)\) のとき、次の問いに答えよ。
(1) \(f(t) = |\vec{a} + t\vec{b}|^2\) とおく。 \(f(t)\) を \(t\) を用いて表せ。
(2) \(f(t)\) の値を最小にする \(t\) の値を求めよ。
(3) (2)で求めた \(t\) の値を \(t_0\) とすると、\(\vec{a} + t_0 \vec{b}\) は \(\vec{b}\) に垂直であることを示せ。

\(f(t)\) は \(t\) の二次関数になります。
二次関数の最小値を求めるときは、おなじみの平方完成を行います。
また、(3) で「垂直である」ことを示すには、ベクトルの垂直条件「内積が \(0\)」を示せばいいですね。
(1)
\(\vec{a} + t\vec{b} = (2t + 1, −t + 1, −t − 1)\)
であるから
\(\begin{align} f(t) &= |\vec{a} + t\vec{b}|^2 \\& = (2t + 1)^2 + (−t + 1)^2 + (−t − 1)^2 \\ &= 6t^2 + 4t + 3 \end{align}\)
答え: \(\color{red}{f(t) = 6t^2 + 4t + 3}\)
(2) \(f(t)\) は \(t\) の二次関数である。
\(f(t)\) を平方完成すると、
\(\begin{align} f(t) &= 6t^2 + 4t + 3 \\ &= 6 \left( t^2 + \frac{2}{3} t \right) + 3 \\ &= 6\left\{ \left(t + \frac{1}{3} \right)^2 − \frac{1}{9} \right\} + 3 \\ &= 6 \left( t + \frac{1}{3} \right)^2 − \frac{2}{3} + 3 \\ &= 6 \left( t + \frac{1}{3} \right)^2 + \frac{7}{3} \end{align}\)
となるので、 \(f(t)\) は \(\displaystyle t = −\frac{1}{3}\) のときに最小値 \(\displaystyle \frac{7}{3}\) をとる。
答え: \(\color{red}{\displaystyle t = −\frac{1}{3}}\)
(3) 証明
(2)より \(\displaystyle t_0 = −\frac{1}{3}\)
\(\vec{a} + t_0 \vec{b}\) と \(\vec{b}\) が垂直であることを示すためには、
\((\vec{a} + t_0 \vec{b}) \cdot \vec{b} = 0\)
を示せばよい。
\(\vec{a} + t_0 \vec{b}\)
\(\displaystyle = \vec{a} − \frac{1}{3} \vec{b}\)
\(\displaystyle = (1, 1, −1) + \left( −\frac{2}{3}, \frac{1}{3}, \frac{1}{3} \right)\)
\(\displaystyle = \left( \frac{1}{3}, \frac{4}{3}, −\frac{2}{3} \right)\)
より
\(\displaystyle \left( \vec{a} − \frac{1}{3} \vec{b} \right) \cdot \vec{b}\)
\(\displaystyle = \left( \frac{1}{3}, \frac{4}{3}, −\frac{2}{3} \right) \cdot (2, −1, −1)\)
\(\displaystyle = \frac{2}{3} − \frac{4}{3} + \frac{2}{3}\)
\(= 0\)
よって、\(\displaystyle \vec{a} + t_0 \vec{b}\) は \(\vec{b}\) に垂直である。
(証明終わり)
以上で問題も終わりです!
空間とはいえ、基本的にやることは平面上のベクトルと同じです。
「空間だから難しい、、、」と弱気にならず、問題演習を通して空間ベクトルに慣れていきましょう!








