この記事では、「楕円」の定義や方程式、グラフについてわかりやすく解説していきます。
また、楕円の焦点や接線の方程式、面積の求め方なども説明していくので、ぜひこの記事を通してマスターしてくださいね!
目次
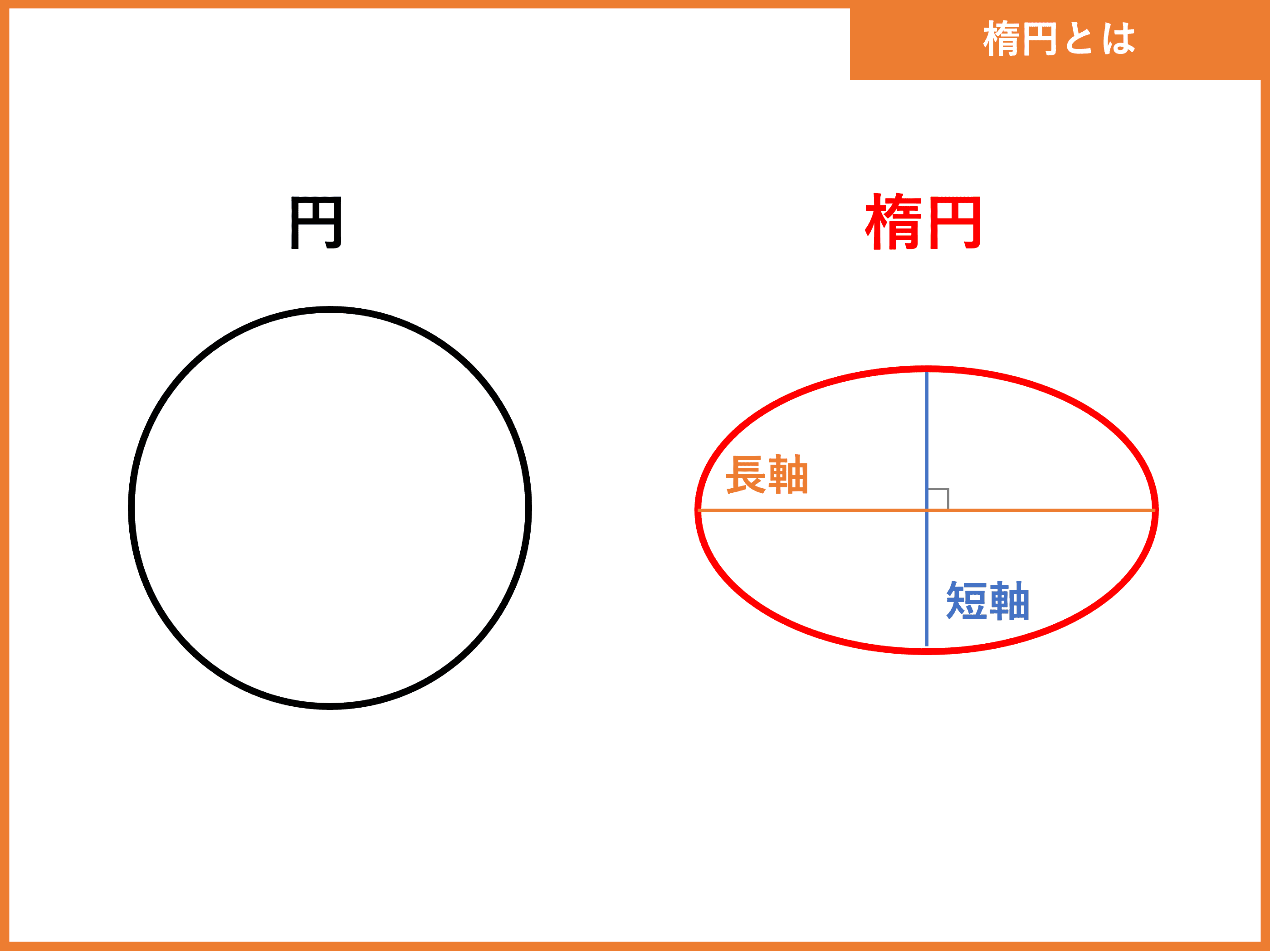
楕円とは?
楕円は、円を押しつぶしたような形をした曲線です。
このとき、楕円の径が最も長い部分の直線を「長軸」、長軸に直行し、最も径が短い部分を「短軸」といいます。
楕円の定義
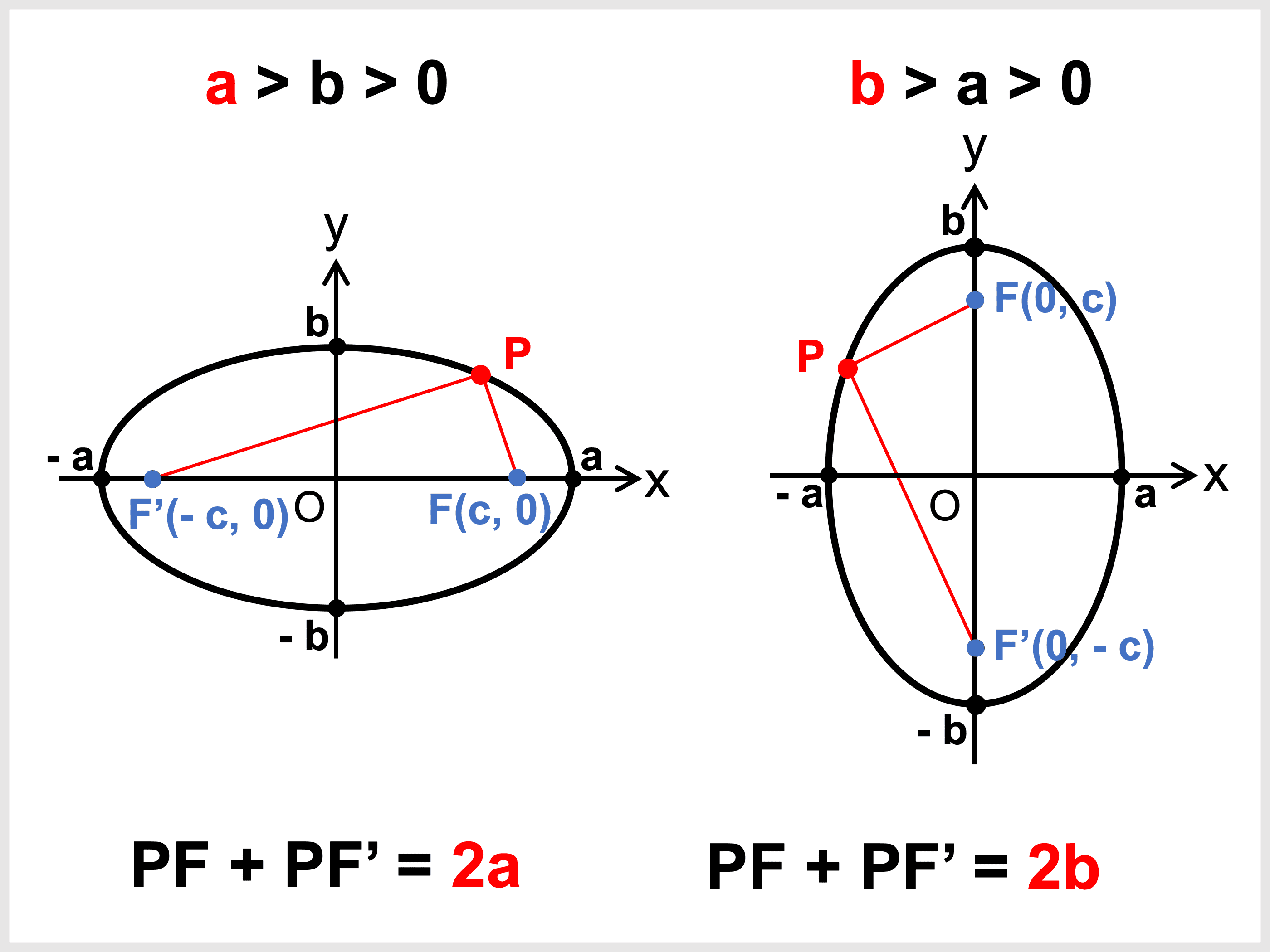
楕円は、\(2\) 定点からの距離の和によって定義されます。
\(2\) 定点 \(\mathrm{F}, \mathrm{F’}\) からの距離の和が一定である点 \(\mathrm{P}\) の軌跡を「楕円」という。
このとき、\(2\) 定点 \(\mathrm{F}, \mathrm{F’}\) を「焦点」という。
距離の和 \(\mathrm{PF} + \mathrm{PF’}\) は、楕円の長軸の長さに等しく、一定です。
- 横長の場合(焦点が \(x\) 軸上):\(\mathrm{PF} + \mathrm{PF’} = 2a\)
- 縦長の場合(焦点が \(y\) 軸上):\(\mathrm{PF} + \mathrm{PF’} = 2b\)
なお、長軸は必ず焦点を通ります。
上記の定義から、楕円の方程式を導くことができます(→ ① 定義から楕円の方程式を求める)。
定義の非常に似ている双曲線と間違えないようにしましょう。
 双曲線とは?方程式やグラフ、焦点・漸近線・接線の求め方
双曲線とは?方程式やグラフ、焦点・漸近線・接線の求め方
楕円の方程式
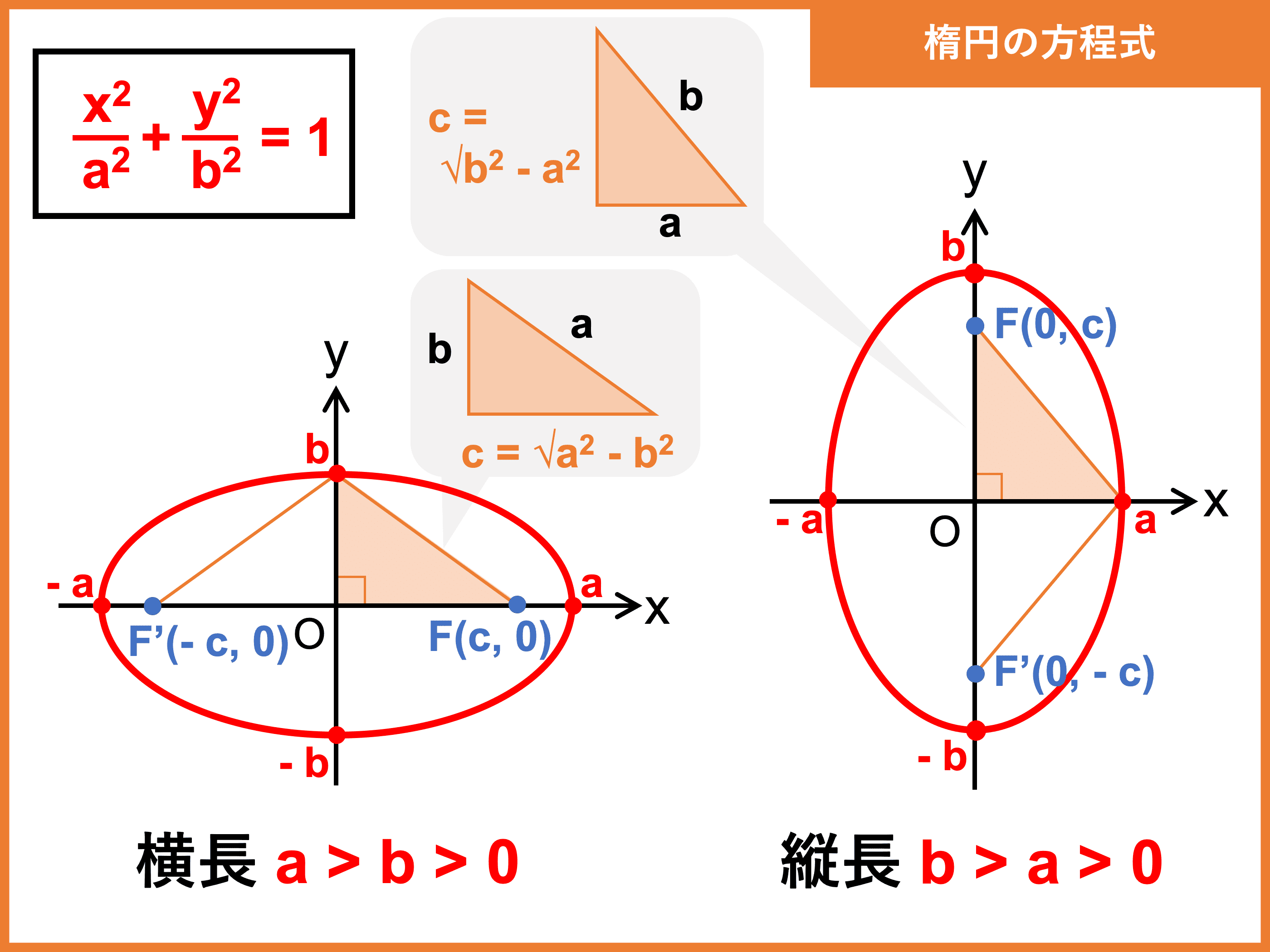
楕円の方程式は \((x \ \text{の項})^2 + (y \ \text{の項})^2 = \pm1\) のかたちで表すことができ、この表し方を「標準形」といいます。
原点を中心にもつ楕円の方程式(標準形)は次のとおりです。
横長の楕円(焦点が \(\bf{x}\) 軸上)
\begin{align}\color{red}{\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ \ (a > b > 0)}\end{align}
- 中心:原点 \((0, 0)\)
- 長軸の長さ:\(2a\)
- 短軸の長さ:\(2b\)
- 焦点:\((\pm c, 0) = (\pm \sqrt{a^2 − b^2}, 0)\)
- 焦点からの距離の和:\(2a\)
縦長の楕円(焦点が \(\bf{y}\) 軸上)
\begin{align}\color{red}{\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ \ (b > a > 0)}\end{align}
- 中心:原点 \((0, 0)\)
- 長軸の長さ:\(2b\)
- 短軸の長さ:\(2a\)
- 焦点:\((0, \pm c) = (0, \pm \sqrt{b^2 − a^2})\)
- 焦点からの距離の和:\(2b\)
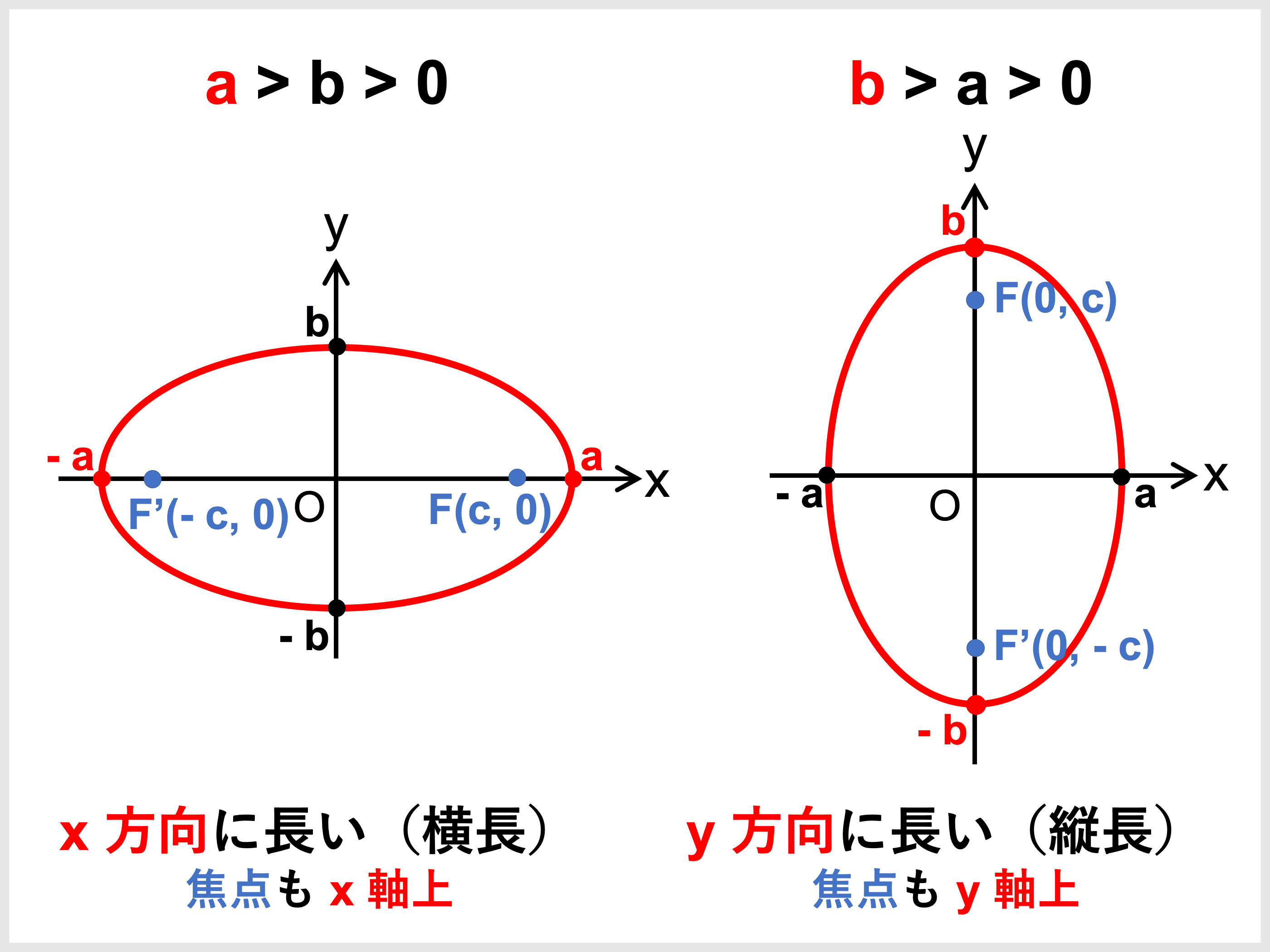
楕円が横長になるか縦長になるかは、\(a\) と \(b\) の大きさによってのみ決まるのですね。
なお、どちらの向きであっても、原点を中心にもつ楕円は \(x\) 軸、\(y\) 軸、原点について対称です。
標準形に対し、かっこがすべて展開されたかたち(\(x\), \(y\) の二次式)を「一般形」といいます。
中心が原点でない楕円の方程式(平行移動)
楕円はほかの曲線と同様、平行移動することができます。
例えば、横長の楕円を平行移動した、中心が原点でない楕円の方程式は次のとおりです。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \ \ (a > b > 0)\) を \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\) だけ平行移動した楕円の方程式は
\begin{align}\color{red}{\displaystyle \frac{(x − p)^2}{a^2} + \frac{(y − q)^2}{b^2} = 1}\end{align}
- 中心:\((p, q)\)
- 長軸の長さ:\(2a\)
- 短軸の長さ:\(2b\)
- 焦点:\((\pm c + p, q) = (\pm \sqrt{a^2 − b^2} + p, q)\)
- 焦点からの距離の和:\(2a\)
縦長の楕円でも、同じように考えることができます。
楕円の基本問題の解き方
ここまでの知識を使って解ける、楕円の基本問題の解き方を解説します。
① 定義から楕円の方程式を求める
(1) \(2\) 定点 \(\mathrm{F}(c, 0)\), \(\mathrm{F’}(−c, 0)\) からの距離の和が \(2a\) となる点の軌跡を求めよ。ただし、定数 \(a, c\) は \(a > c > 0\) を満たす。
(2) \(2\) 定点 \(\mathrm{F}(0, c)\), \(\mathrm{F’}(0, −c)\) からの距離の和が \(2b\) となる点の軌跡を求めよ。ただし、定数 \(b, c\) は \(b > c > 0\) を満たす。
楕円の定義式(距離の和に関する条件式)を変形していくと、楕円の方程式を導くことができます。
(見切れる場合は横へスクロール)
求める軌跡上の動点を \(\mathrm{P}(x, y)\) とおく。
点 \(\mathrm{P}(x, y)\), \(\mathrm{F}(c, 0)\), \(\mathrm{F’}(−c, 0)\) において、
\(2\) 点間の距離 \(\mathrm{PF}\) および \(\mathrm{PF’}\) は
\(\begin{align}\mathrm{PF} &= \sqrt{(x − c)^2 + (y − 0)^2} \\&= \sqrt{(x − c)^2 + y^2}\end{align}\)
\(\begin{align}\mathrm{PF’} &= \sqrt{\{x − (−c)\}^2 + (y − 0)^2} \\&= \sqrt{(x + c)^2 + y^2}\end{align}\)
条件 \(\mathrm{PF} + \mathrm{PF’} = 2a\) より、
\(\sqrt{(x − c)^2 + y^2} + \sqrt{(x + c)^2 + y^2} = 2a\)
移項して
\(\sqrt{(x − c)^2 + y^2} = 2a − \sqrt{(x + c)^2 + y^2} \)
両辺を \(2\) 乗して
\((x − c)^2 + y^2 = 4a^2 − 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2\)
展開して
\(x^2 − 2cx + c^2 + y^2 = 4a^2 − 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 + y^2\)
両辺から \(x^2\), \(c^2\), \(y^2\) を消去して
\(− 2cx = 4a^2 − 4a\sqrt{(x + c)^2 + y^2} + 2cx\)
移項して
\(4a\sqrt{(x + c)^2 + y^2} = 4a^2 + 4cx\)
両辺を \(4\) で割って
\(a\sqrt{(x + c)^2 + y^2} = a^2 + cx\)
両辺を \(2\) 乗して
\(a^2\{(x + c)^2 + y^2\} = a^4 + 2a^2cx + c^2x^2\)
展開して
\(a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2\)
\(a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2\)
両辺から \(2a^2cx\) を消去して
\(a^2x^2 + a^2c^2 + a^2y^2 = a^4 + c^2x^2\)
移項、整理して
\(a^2x^2 − c^2x^2 + a^2y^2 = a^4 − a^2c^2\)
\((a^2 − c^2)x^2 + a^2y^2 = a^2(a^2 − c^2)\)
ここで、両辺を \(a^2(a^2 − c^2)\) \((> 0)\) で割ると
\(\color{red}{\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2 − c^2} = 1}\)
この曲線上のすべての点は \(\mathrm{PF} + \mathrm{PF’} = 2a\) を満たす。
なお、\(a^2 − c^2 = b^2\) とおくと、
楕円の方程式の標準形 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((a > b > 0)\) が得られ、
\(c = \pm\sqrt{a^2 − b^2}\) より、焦点 \(\mathrm{F}\), \(\mathrm{F’}\) の座標は
- \(\mathrm{F}(c, 0) = (\sqrt{a^2 − b^2}, 0)\)
- \(\mathrm{F’}(−c, 0) = (−\sqrt{a^2 − b^2}, 0)\)
と表すことができます。
(見切れる場合は横へスクロール)
求める軌跡上の動点を \(\mathrm{P}(x, y)\) とおく。
点 \(\mathrm{P}(x, y)\), \(\mathrm{F}(0, c)\), \(\mathrm{F’}(0, −c)\) において、
\(2\) 点間の距離 \(\mathrm{PF}\) および \(\mathrm{PF’}\) は
\(\begin{align}\mathrm{PF} &= \sqrt{(x − 0)^2 + (y − c)^2} \\&= \sqrt{x^2 + (y − c)^2}\end{align}\)
\(\begin{align}\mathrm{PF’} &= \sqrt{(x − 0)^2 + \{y − (− c)\}^2} \\&= \sqrt{x^2 + (y + c)^2}\end{align}\)
条件 \(\mathrm{PF} + \mathrm{PF’} = 2b\) より、
\(\sqrt{x^2 + (y − c)^2} + \sqrt{x^2 + (y + c)^2} = 2b\)
移項して
\(\sqrt{x^2 + (y − c)^2} = 2b − \sqrt{x^2 + (y + c)^2} \)
両辺を \(2\) 乗して
\(x^2 + (y − c)^2 = 4b^2 − 4b\sqrt{x^2 + (y + c)^2} + x^2 + (y + c)^2\)
展開して
\(x^2 + y^2 − 2cy + c^2 = 4b^2 − 4b\sqrt{x^2 + (y + c)^2} + x^2 + y^2 + 2cy + c^2\)
両辺から \(x^2\), \(y^2\), \(c^2\) を消去して
\(− 2cy = 4b^2 − 4b\sqrt{x^2 + (y + c)^2} + 2cy\)
移項して
\(4b\sqrt{x^2 + (y + c)^2} = 4b^2 + 4cy\)
両辺を \(4\) で割って
\(b\sqrt{x^2 + (y + c)^2} = b^2 + cy\)
両辺を \(2\) 乗して
\(b^2\{x^2 + (y + c)^2\} = b^4 + 2b^2cy + c^2y^2\)
展開して
\(b^2(x^2 + y^2 + 2cy + c^2) = b^4 + 2b^2cy + c^2y^2\)
\(b^2x^2 + b^2y^2 + 2b^2cy + b^2c^2 = b^4 + 2b^2cy + c^2y^2\)
両辺から \(2b^2cy\) を消去して
\(b^2x^2 + b^2y^2 + b^2c^2 = b^4 + c^2y^2\)
移項、整理して
\(b^2x^2 + b^2y^2 − c^2y^2 = b^4 − b^2c^2\)
\(b^2x^2 + (b^2 − c^2)y^2 = b^2(b^2 − c^2)\)
ここで、両辺を \(b^2(b^2 − c^2)\) \((> 0)\) で割ると
\(\color{red}{\displaystyle \frac{x^2}{b^2 − c^2} + \frac{y^2}{b^2} = 1}\)
この曲線上のすべての点は \(\mathrm{PF} + \mathrm{PF’} = 2b\) を満たす。
こちらも \(b^2 − c^2 = a^2\) とおくと、標準形 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((b > a > 0)\) が得られ、
\(c = \pm\sqrt{b^2 − a^2}\) より、焦点 \(\mathrm{F}\), \(\mathrm{F’}\) の座標は
- \(\mathrm{F}(0, c) = (0, \sqrt{b^2 − a^2})\)
- \(\mathrm{F’}(0, −c) = (0, −\sqrt{b^2 − a^2})\)
と表すことができます。
② 楕円の焦点・長軸・短軸の求め方(標準形)
標準形で表された楕円の焦点の座標、および長軸・短軸の長さの求め方を説明します。
楕円 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) の焦点の座標、長軸・短軸の長さを求めよ。
\(x\) の項と \(y\) の項の分母の大きさを比較して、楕円の向きが横長か縦長かを特定します。
\(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) において、\(a > b > 0\) ならば横長、\(b > a > 0\) ならば縦長の楕円でしたね。
問題の方程式 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) は \(\sqrt{12} > \sqrt{4}\) なので、横長の楕円、つまり、「長軸・焦点は \(x\) 軸上にある」と意識しておきます。
\(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((a > b > 0)\) における長軸の長さは \(2a\)、短軸の長さは \(2b\) です。
分母の平方根に注目しましょう。
\(\displaystyle \frac{x^2}{(2\sqrt{3})^2} + \frac{y^2}{2^2} = 1\) から、
長軸の長さは \(2 \cdot 2\sqrt{3} = 4\sqrt{3}\)
短軸の長さは \(2 \cdot 2 = 4\)
\(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) における焦点の座標は \((\pm \sqrt{a^2 − b^2}, 0)\) です。
つまり、\(x\) の項と \(y\) の項の分母の差の平方根が、焦点の \(x\) 座標ですね。
\(\sqrt{12 − 4} = \sqrt{8} = 2\sqrt{2}\) より
焦点の座標は \((2\sqrt{2}, 0)\)、\((−2\sqrt{2}, 0)\)
\(\displaystyle \frac{x^2}{(2\sqrt{3})^2} + \frac{y^2}{2^2} = 1\) から、
長軸の長さは \(2 \cdot 2\sqrt{3} = 4\sqrt{3}\)
短軸の長さは \(2 \cdot 2 = 4\)
\(\sqrt{12 − 4} = \sqrt{8} = 2\sqrt{2}\) より
焦点の座標は \((2\sqrt{2}, 0)\)、\((−2\sqrt{2}, 0)\)
答え:
長軸の長さ \(\color{red}{4\sqrt{3}}\)、短軸の長さ \(\color{red}{4}\)
焦点 \(\color{red}{(2\sqrt{2}, 0)}\)、\(\color{red}{(−2\sqrt{2}, 0)}\)
③ 楕円の焦点・長軸・短軸の求め方(一般形)
一般形で表された楕円の焦点の座標、および長軸・短軸の長さの求め方を説明します。
楕円 \(x^2 + 4y^2 + 4x − 24y + 36 = 0\) の焦点の座標、長軸・短軸の長さを求めよ。
一般形で楕円の方程式が与えられた場合は、まず標準形に変形します。
\((x \ \text{の項})^2 + (y \ \text{の項})^2 = ◯\) のかたちになるよう、\(x\), \(y\) それぞれについて平方完成します。
平方完成の外に出た定数部分は右辺にもっていきます。
(見切れる場合は横へスクロール)
\(x^2 + 4y^2 + 4x − 24y + 36 = 0\)
\(x^2 + 4x + 4y^2 − 24y + 36 = 0\)
\((x^2 + 4x + 4) − 4 + 4(y^2 − 6y + 9) − 4 \cdot 9 + 36 = 0\)
\((x + 2)^2 − 4 + 4(y − 3)^2 − 36 + 36 = 0\)
\((x + 2)^2 + 4(y − 3)^2 = 4\)
右辺が \(1\) になるよう、両辺を同じ数で割ります。
そうすると、楕円の方程式の標準形 \(\displaystyle \frac{(x − p)^2}{a^2} + \frac{(y − q)^2}{b^2} = 1\) が得られます。
\((x + 2)^2 + 4(y − 3)^2 = 4\)
両辺を \(4\) で割って
\(\displaystyle \frac{(x + 2)^2}{4} + (y − 3)^2 = 1\)
原点を中心にもつ楕円をどれだけ平行移動したものかを求めます。
楕円 \(\displaystyle \frac{(x − p)^2}{a^2} + \frac{(y − q)^2}{b^2} = 1\) は、楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) を \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\) だけ平行移動したものでしたね。
\(\displaystyle \frac{(x + 2)^2}{4} + (y − 3)^2 = 1\) は
楕円 \(\displaystyle \frac{x^2}{4} + y^2 = 1\) を \(x\) 軸方向に \(−2\)、\(y\) 軸方向に \(3\) だけ平行移動したものである。
分母の平方根の大小関係に注目し、横長か縦長かを見極めた上で長軸・短軸の長さを求めます。
この問題では \(\sqrt{4} = 2 > \sqrt{1} = 1\) なので横長、つまり「長軸・焦点が \(x\) 軸上にある」楕円ですね。
\(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((a > b > 0)\) における長軸の長さは \(2a\)、短軸の長さは \(2b\) です。
\(\displaystyle \frac{(x + 2)^2}{2^2} + \frac{(y − 3)^2}{1^2} = 1\) \((2 > 1 > 0)\) から、
長軸の長さは \(2 \times 2 = 4\)
短軸の長さは \(1 \times 2 = 2\)
\(\displaystyle \frac{(x − p)^2}{a^2} + \frac{(y − q)^2}{b^2} = 1\) \((a > b > 0)\) における焦点の座標は \((\pm \sqrt{a^2 − b^2} + p, q)\) です。
\(x\) の項と \(y\) の項の分母の差の平方根 \(\pm \sqrt{a^2 − b^2}\) と、平行移動量 \((p, q)\) に注目しましょう。
\(\displaystyle \frac{(x + 2)^2}{4} + (y − 3)^2 = 1\)
(楕円 \(\displaystyle \frac{x^2}{4} + y^2 = 1\) を \(x\) 軸方向に \(−2\)、\(y\) 軸方向に \(3\) だけ平行移動したもの)
\(\sqrt{4 − 1} = \sqrt{3}\) より
焦点は \((\sqrt{3} − 2, 3)\)、\((−\sqrt{3} − 2, 3)\)
(見切れる場合は横へスクロール)
\(x^2 + 4y^2 + 4x − 24y + 36 = 0\)
\(x^2 + 4x + 4y^2 − 24y + 36 = 0\)
\((x^2 + 4x + 4) − 4 + 4(y^2 − 6y + 9) − 4 \cdot 9 + 36 = 0\)
\((x + 2)^2 − 4 + 4(y − 3)^2 − 36 + 36 = 0\)
\((x + 2)^2 + 4(y − 3)^2 = 4\)
\(\displaystyle \frac{(x + 2)^2}{4} + (y − 3)^2 = 1\)
よって、この楕円は
楕円 \(\displaystyle \frac{x^2}{4} + y^2 = 1\) を \(x\) 軸方向に \(−2\)、\(y\) 軸方向に \(3\) だけ平行移動したものである。
\(\displaystyle \frac{(x + 2)^2}{2^2} + \frac{(y − 3)^2}{1^2} = 1\) から、
長軸の長さは \(2 \times 2 = 4\)
短軸の長さは \(1 \times 2 = 2\)
また、
\(\sqrt{4 − 1} = \sqrt{3}\) より
焦点は \((\sqrt{3} − 2, 3)\)、\((−\sqrt{3} − 2, 3)\)
答え:
長軸の長さ \(\color{red}{4}\)、短軸の長さ \(\color{red}{2}\)
焦点 \(\color{red}{(\sqrt{3} − 2, 3)}\)、\(\color{red}{(−\sqrt{3} − 2, 3)}\)
④ 焦点から楕円の方程式を求める
\(2\) 点 \((0, 2)\), \((0, −2)\) を焦点とし、長軸の長さが \(6\) である楕円の方程式を求めよ。
焦点が \(x\) 軸上、\(y\) 軸上のどちらにあるかを考えて、定数 \(a\), \(b\) を使って楕円の方程式を自分で設定します。
長軸の長さ、焦点の座標から定数 \(a\), \(b\) を求めます。
(見切れる場合は横へスクロール)
焦点が \(y\) 軸上にあるから、求める楕円の方程式は \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((b > a > 0)\) とおける。
長軸の長さ \(2b = 6\) より
\(b = 3\)
焦点について、\(\sqrt{b^2 − a^2} = 2\) より
\(a^2 = b^2 − 4 = 9 − 4 = 5\)
よって、求める楕円の方程式は
\(\displaystyle \frac{x^2}{5} + \frac{y^2}{9} = 1\)
答え: \(\color{red}{\displaystyle \frac{x^2}{5} + \frac{y^2}{9} = 1}\)
楕円のグラフの書き方
次の例題を通して、楕円のグラフを書く手順を解説します。
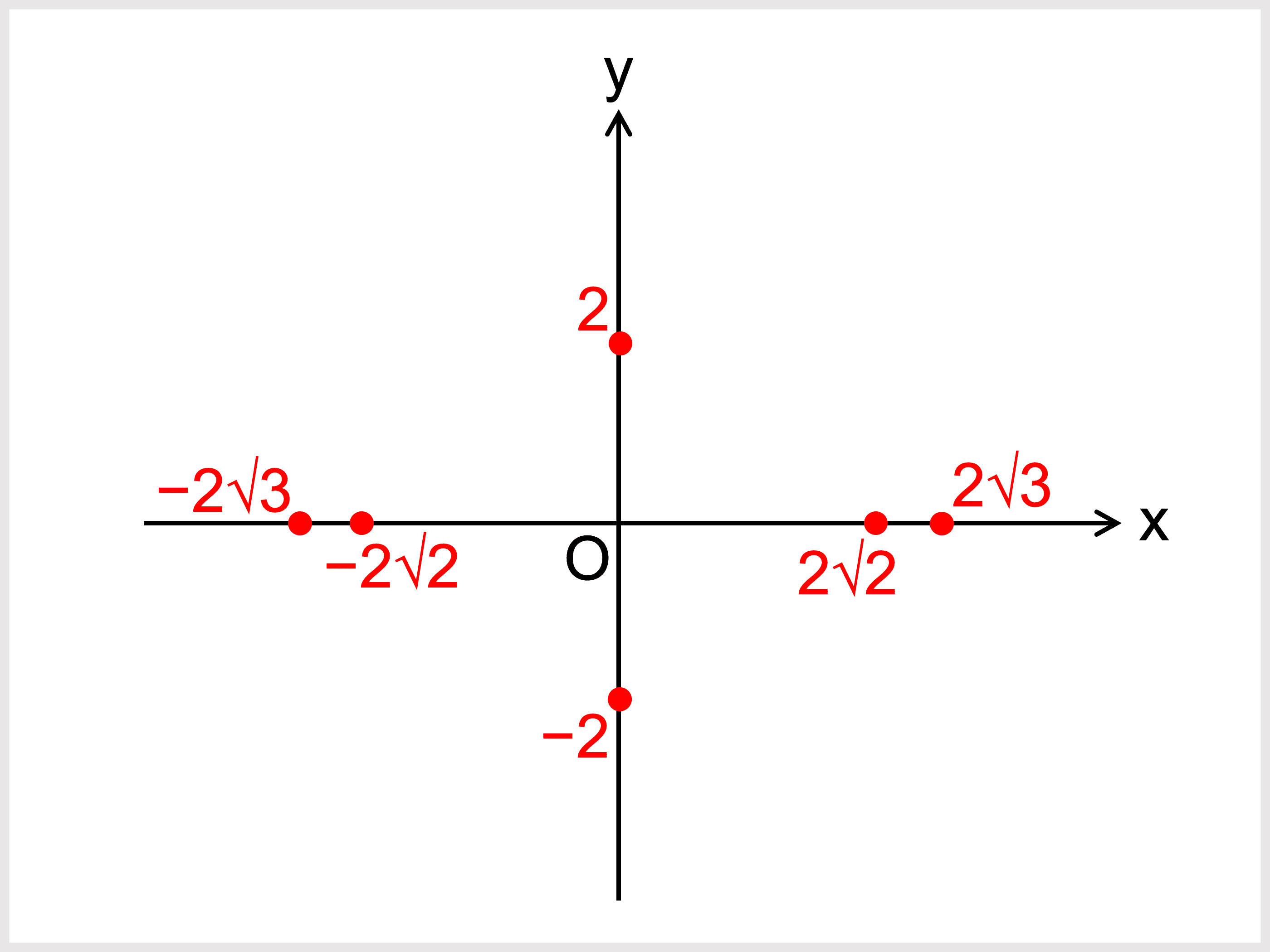
楕円 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) のグラフを書け。
まずは、楕円の向きが横長か縦長かを特定します。
楕円の方程式 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) において、\((a > b > 0)\) のときは横長(焦点が \(x\) 軸上)、\((b > a > 0)\) のときは縦長(焦点が \(y\) 軸上)のグラフとなります。
「分母が大きい方が長軸となる」ことを覚えておきましょう。
例題 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) では、\(x\) の項の分母の方が大きいので横長の楕円、つまり、「焦点は \(x\) 軸上にある」と意識しておきます。
長軸・短軸の長さと焦点の座標を求めておきます。
\(\displaystyle \frac{x^2}{(2\sqrt{3})^2} + \frac{y^2}{2^2} = 1\) から、
長軸の長さは \(2\sqrt{3} \times 2 = 4\sqrt{3}\)
短軸の長さは \(2 \times 2 = 4\)
\(\sqrt{12 − 4} = \sqrt{8} = 2\sqrt{2}\)
焦点の座標は \((2\sqrt{2}, 0)\)、\((−2\sqrt{2}, 0)\)
座標平面を用意し、求めておいた焦点、および長軸と短軸の両端の点(中心からの距離がそれぞれ \(a\), \(b\) の点)を打ちます。
焦点はなくてもグラフは書けますが、示しておく方が無難です。
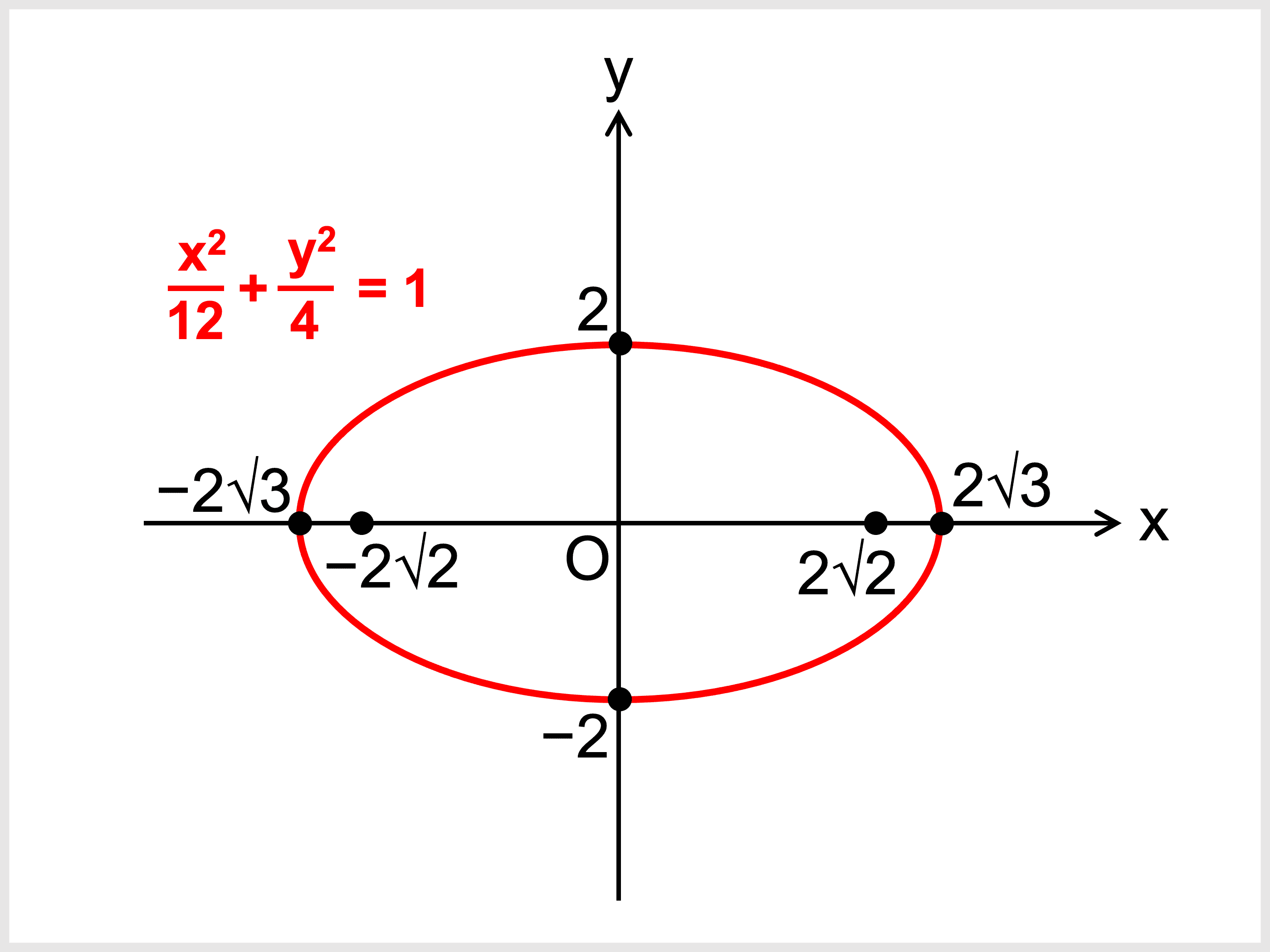
最後に、楕円を描けばグラフの完成です。
長軸と短軸の両端を通るなめらかな曲線を描きましょう。
楕円の接線の方程式
楕円の接線の方程式には、任意の点 \((x_1, y_1)\) が与えられた場合と、傾き \(m\) が与えられた場合の \(2\) 通りの表し方があります。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) の接線の方程式は、以下のように与えられる。
- 点 \((x_1, y_1)\) における接線の方程式
\begin{align}\color{red}{\frac{x_1x}{a^2} + \frac{y_1y}{b^2} = 1}\end{align} - 傾き \(m\) の接線の方程式
\begin{align}y = mx \pm \sqrt{a^2m^2 + b^2}\end{align}
問題でよく使うのは圧倒的に赤字の公式なので、そちらを重点的に覚えておきましょう。
「接線の方程式」については、以下の記事でより詳しく説明しています。
 接線、接線の方程式とは?公式や微分による傾きの求め方
接線、接線の方程式とは?公式や微分による傾きの求め方
楕円の接線の方程式の求め方
次の例題で、楕円の接線の方程式の求め方を説明します。
楕円 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) について、以下の問いに答えよ。
(1) 楕円上の点 \((\sqrt{3}, \sqrt{3})\) における接線の方程式を求めよ。
(2) 点 \((−1, 3)\) から楕円に引いた接線の方程式を求めよ。
\(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) の点 \((x_1, y_1)\) における接線の方程式は \(\displaystyle \frac{x_1x}{a^2} + \frac{y_1y}{b^2} = 1\) です。
つまり、\(x\), \(y\) の \(1\) つずつを接点の座標 \(x_1\), \(y_1\) で置き換えるだけですね。
(2) では、接点を \((x_1, y_1)\) とおいて接線の方程式を立ててから、通る点の座標を代入します。
楕円 \(\displaystyle \frac{x^2}{12} + \frac{y^2}{4} = 1\) の点 \((\sqrt{3}, \sqrt{3})\) における接線の方程式は、
\(\displaystyle \frac{\sqrt{3}x}{12} + \frac{\sqrt{3}y}{4} = 1\)
\(x + 3y = \displaystyle \frac{12}{\sqrt{3}}\)
\(x + 3y = 4\sqrt{3}\)
(\(y =\) 〜 のかたちに変形する場合は以下)
\(y = −\displaystyle \frac{1}{3}x + \displaystyle \frac{4\sqrt{3}}{3}\)
答え:
\(x + 3y = 4\sqrt{3}\)
(\(y = −\displaystyle \frac{1}{3}x + \displaystyle \frac{4\sqrt{3}}{3}\))
接点の座標を \((x_1, y_1)\) とおくと、
接線の方程式は
\(\displaystyle \frac{x_1 x}{12} + \frac{y_1 y}{4} = 1\)
すなわち
\(x_1 x + 3y_1 y = 12\) …①
これが点 \((−1, 3)\) を通るから
\(−x_1 + 9y_1 = 12\)
よって
\(x_1 = 9y_1 − 12\) …②
また、接点は楕円上にあるから
\(x_1^2 + 3y_1^2 = 12\)
②を代入すると
\((9y_1 − 12)^2 + 3y_1^2 = 12\)
\(81y_1^2 − 216y_1 + 144 + 3y_1^2 = 12\)
\(84y_1^2 − 216y_1 + 132 = 0\)
\(7y_1^2 − 18y_1 + 11 = 0\)
因数分解すると
\((y_1 − 1)(7y_1 − 11) = 0\)
よって
\(\displaystyle y_1 = 1, \frac{11}{7}\)
②より、
\(y_1 = 1\) のとき \(x_1 = 9 − 12 = −3\)
\(\displaystyle y_1 = \frac{11}{7}\) のとき \(\displaystyle x_1 = \frac{99}{7} − 12 = \frac{15}{7}\)
それぞれ①に代入すると、接線の方程式は
\(−3x + 3y = 12\)、\(\displaystyle \frac{15}{7}x + \frac{33}{7}y = 12\)
すなわち
\(x − y = −4\)、\(5x + 11y = 28\)
答え:
\(x − y = −4\)、\(5x + 11y = 28\)
楕円の媒介変数表示
楕円は媒介変数表示もできます。
三角関数を使った以下の媒介変数表示が有名です。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) の媒介変数表示は、
\begin{align}\color{red}{\left\{\begin{array}{l}x = a\cos \theta\\y = b\sin \theta \end{array}\right.}\end{align}
楕円の媒介変数表示は、円の媒介変数表示から導けます。
円の媒介変数表示は、単位円でおなじみですね。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) は、半径 \(a\) の円 \(x^2 + y^2 = a^2\) を \(y\) 軸方向に \(\displaystyle \frac{b}{a}\) 倍したものである。
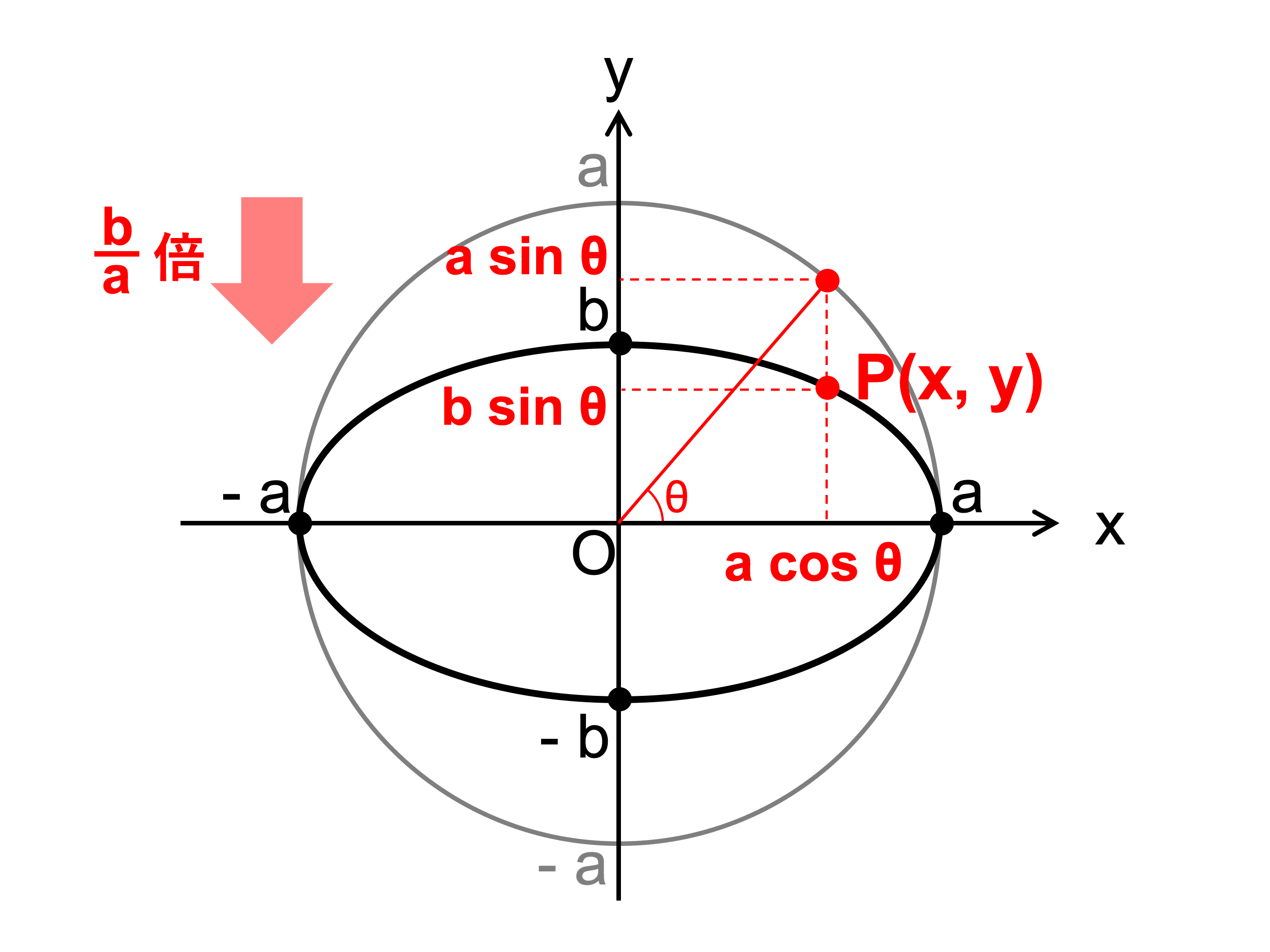
よって、円 \(x^2 + y^2 = a^2\) 上の点 \((a\cos\theta, a\sin\theta)\) に対して、\(y\) 軸方向に \(\displaystyle \frac{b}{a}\) 倍した点を \(\mathrm{P}(x, y)\) とすると、
\begin{align}\left\{\begin{array}{l}x = \color{red}{a\cos \theta}\\y = a\sin\theta \times \displaystyle \frac{b}{a} = \color{red}{b\sin \theta} \end{array}\right.\end{align}
(証明終わり)
媒介変数表示の仕方は \(1\) 通りとは限りません。
例えば、楕円には以下のような媒介変数表示もあります。
- \(\left\{\begin{array}{l} \displaystyle x = a \cdot \frac{1 − t^2}{1 + t^2}\\ \displaystyle y = b \cdot \frac{2t}{1 + t^2}\end{array}\right.\)
媒介変数表示された曲線の形を答える問題もあるので、柔軟に対応できるようにしておきましょう。
「媒介変数表示」については以下の記事で説明しています。
 媒介変数表示とは?グラフや計算(微分積分・ベクトル)
媒介変数表示とは?グラフや計算(微分積分・ベクトル)
媒介変数表示が示す曲線の求め方
次の例題で、媒介変数表示された楕円を標準形に直す方法を説明します。
次の媒介変数表示が示す曲線を答えよ。
(1) \(x = 3\cos\theta + 2\), \(y = 4\sin\theta + 1\)
(2) \(x = \sqrt{2t}\), \(y = \sqrt{1 − t}\)
与えられた式を変形して、媒介変数を消去します。
媒介変数が角(\(\theta\) など)のときは、三角関数の性質を利用するとうまくいきます。
\(x = 3\cos\theta + 2\) より
\(\displaystyle \cos\theta = \frac{x − 2}{3}\) …①
\(y = 4\sin\theta + 1\) より
\(\displaystyle \sin\theta = \frac{y − 1}{4}\) …②
三角関数の相互関係より
\(\sin^2\theta + \cos^2\theta = 1\)
①、②を代入して
\(\displaystyle \frac{(x − 2)^2}{9} + \frac{(y − 1)^2}{16} = 1\)
答え: 楕円 \(\color{red}{\displaystyle \frac{(x − 2)^2}{9} + \frac{(y − 1)^2}{16} = 1}\)
右辺が正の平方根であることに注目すると、両辺を \(2\) 乗できます。
\(x = \sqrt{2t} \geq 0\), \(y = \sqrt{1 − t} \geq 0\) より
両辺を \(2\) 乗して
\(x^2 = 2t\)
\(y^2 = 1 − t\)
よって
\(\displaystyle y^2 = 1 − \frac{x^2}{2}\)
\(\displaystyle \frac{x^2}{2} + y^2 = 1\)
したがって、楕円 \(\displaystyle \frac{x^2}{2} + y^2 = 1\) の \(x \geq 0\), \(y \geq 0\) の部分である。
答え:
楕円 \(\color{red}{\displaystyle \frac{x^2}{2} + y^2 = 1}\) \(\color{red}{(x \geq 0, y \geq 0)}\)
楕円の面積の公式
楕円の面積は次の公式で求められます。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((a > 0, b > 0)\) の面積 \(S\) は
\begin{align}\color{red}{S = \pi ab}\end{align}
楕円 \(\displaystyle \frac{x^2}{3} + \frac{y^2}{16} = 1\) の面積を求めよ。
求める面積を \(S\) とおくと、
\(\displaystyle \frac{x^2}{\sqrt{3}^2} + \frac{y^2}{4^2} = 1\) より
\(S = \pi \cdot \sqrt{3} \cdot 4 = 4\sqrt{3}\pi\)
答え: \(4\sqrt{3}\pi\)
この公式、円の面積の公式「\(S = \pi r^2\)」に似ていますね。
実際に、楕円の面積の公式に \(a = b = r\) を代入すると、円の面積の公式に一致します。
\(a = b = r\) のとき、
\(\displaystyle \frac{x^2}{r^2} + \frac{y^2}{r^2} = 1\)
\(x^2 + y^2 = r^2\) (半径 \(r\) の円)
面積 \(S\) は
\(S = \pi \cdot r \cdot r = \pi r^2\)
ちなみに、楕円の周長を求める公式は円周(円の周長)の公式に比べて非常に複雑なため、問題として聞かれることは少ないです。
なお、「曲線の長さの求め方」については以下の記事を参考にしてください。
 曲線の長さの求め方を解説!積分公式と証明、問題の解き方
曲線の長さの求め方を解説!積分公式と証明、問題の解き方
楕円の面積の公式は、主に \(2\) 通りの方法で導くことができます。
楕円の面積公式の証明① 拡大・縮小
\(1\) つ目は、円を拡大・縮小して楕円の面積を求める方法です。
ただし、この証明では円の面積の公式 \(S = \pi r^2\) が成り立つことが前提です。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) の両辺を \(a^2\) 倍して
\(x^2 + \displaystyle \frac{a^2y^2}{b^2} = a^2\)
\(x^2 + \left(\displaystyle \frac{a}{b}y \right)^2 = a^2\)
これは、半径 \(a\) の円 \(x^2 + y^2 = a^2\) を \(y\) 軸方向に \(\displaystyle \frac{b}{a}\) 倍したものである。
図形を縦に \(\displaystyle \frac{b}{a}\) 倍すると、面積も \(\displaystyle \frac{b}{a}\) 倍になるので、楕円の面積 \(S\) は
\(\begin{align}S &= \pi a^2 \times \displaystyle \frac{b}{a} \\&= \color{red}{\pi ab}\end{align}\)
(証明終わり)
楕円の面積公式の証明② 積分
\(2\) つ目は、楕円の面積を積分で直接求める方法です。
置換積分法を使って計算します。
楕円 \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) を \(y\) について解くと
\(y = \pm b\sqrt{1 − \displaystyle \frac{x^2}{a^2}}\)
楕円は \(x\) 軸、\(y\) 軸について対称であるから、楕円の面積 \(S\) は図の斜線部の \(4\) 倍である。
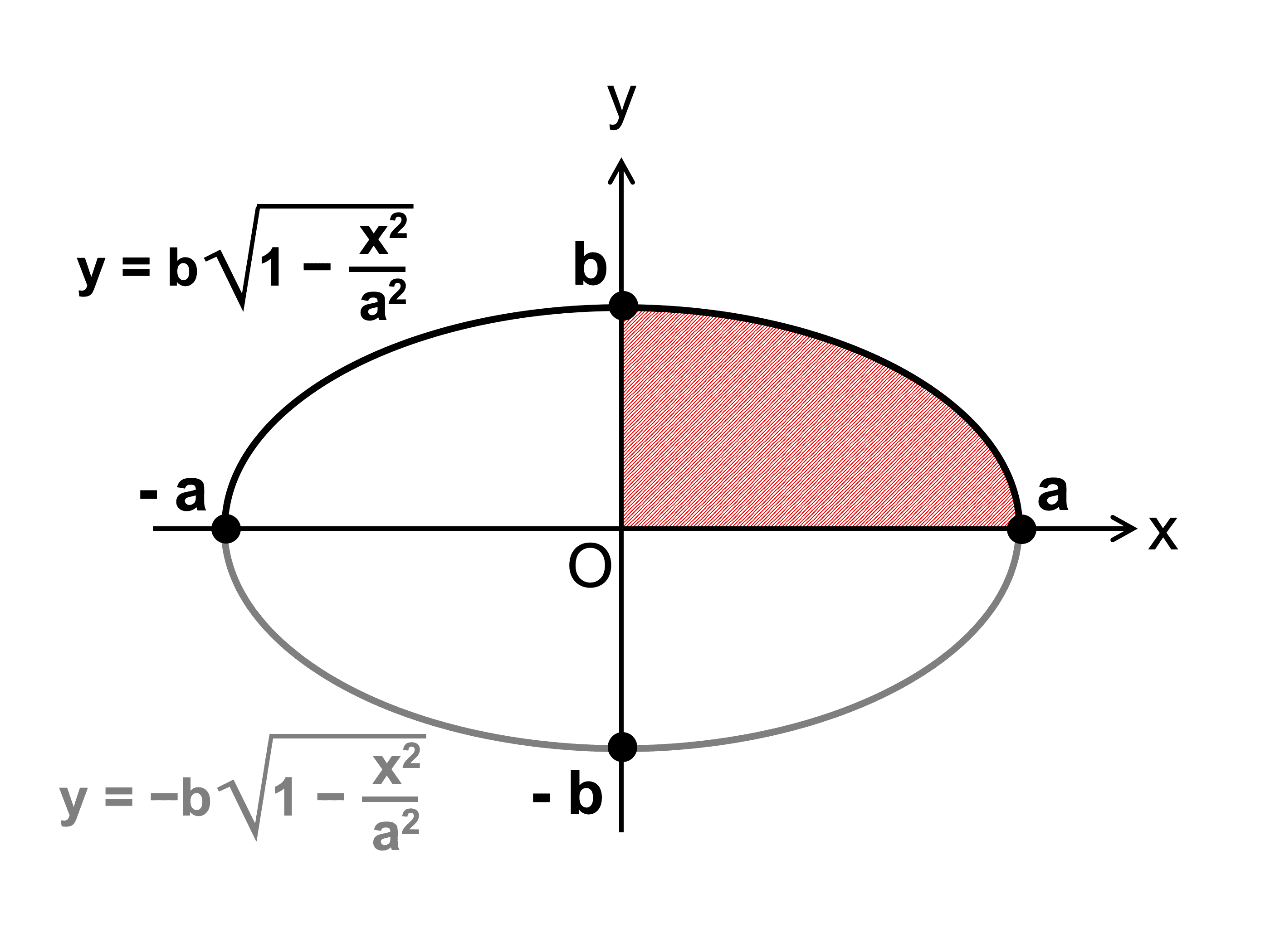
よって、
\(S = \displaystyle 4\int_0^{a}b\sqrt{1 − \frac{x^2}{a^2}} \ dx\)
ここで、\(x = a\sin\theta\) とおくと
\(\displaystyle \frac{dx}{d\theta} = a \cos\theta\)
よって \(dx = a \cos\theta \, d\theta\)
| \(x\) | \(0 \longrightarrow a\) |
|---|---|
| \(\theta\) | \(0 \longrightarrow \displaystyle \frac{\pi}{2}\) |
\(0 \leq \theta \leq \displaystyle \frac{\pi}{2}\) において、\(\cos\theta \geq 0\) より
\(\begin{align}\displaystyle \sqrt{1 − \frac{x^2}{a^2}} &= \sqrt{1 − \frac{a^2\sin^2\theta}{a^2}} \\&= \sqrt{1 − \sin^2\theta} \\&= \cos\theta\end{align}\)
よって
\(\begin{align}S &= \displaystyle 4\int_0^{a}b\sqrt{1 − \frac{x^2}{a^2}}\, dx \\&= 4\int_{0}^{\frac{\pi}{2}} b\cos\theta \cdot a\cos\theta \, d\theta \\&= 4ab\int_{0}^{\frac{\pi}{2}} \cos^2\theta \, d\theta \\&= 2ab\int_{0}^{\frac{\pi}{2}} (1 + \cos 2\theta) \, d\theta \\&= 2ab \left[ \theta + \frac{1}{2}\sin2\theta \right]_0^{\frac{\pi}{2}} \\&= 2ab \left\{ \left( \frac{\pi}{2} + 0 \right) − (0 + 0) \right\} \\&= \color{red}{\pi ab}\end{align}\)
(証明終わり)
以上で解説は終わりです!
方程式が複雑な楕円ですが、定義や特徴を押さえておけば怖くありません。
他の曲線と合わせて、しっかりと理解してくださいね!


