この記事では、「カージオイド・サイクロイド」などの有名な曲線のグラフや式を一覧で示していきます。
それぞれの定義や特徴、関連性を簡潔にわかりやすく説明していきますので、ぜひこの記事を通して理解を深めてくださいね。
目次
有名な曲線の式一覧
ここでは、高校の教科書でも名前を見ることがある有名な曲線の式の一覧を示します。
気になる曲線があればクリックして曲線の定義やグラフの概形を確認してくださいね!
(表が見切れる場合は横へスクロール)
ここで紹介する曲線は、数ある曲線のうちのほんの一部です。
また、式のうち、複雑なもの、およびその形式では表せないものは省略しています。
| 総称 | 曲線名 | 方程式(直交座標) | 媒介変数表示 | 極方程式 |
|---|---|---|---|---|
| 円錐曲線 | 円 | \(x^2 + y^2 = a^2\) | \(\left\{\begin{array}{l} x = a\cos\theta\\ y = a\sin\theta\end{array}\right.\) | \(r = a\) |
| 楕円 | \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) | \(\left\{\begin{array}{l}x = a\cos\theta\\ y = b\sin\theta\end{array}\right.\) | \(\displaystyle r = \frac{l}{1 + e\cos\theta}\)
\(l \,(> 0)\) : 半直弦 \(e\) : 離心率 |
|
| 放物線 | \(y^2 = 4px\) (標準形) |
\(\left\{\begin{array}{l} x = pt^2\\ y = 2pt\end{array}\right.\) | ||
| 双曲線 | \(\displaystyle \frac{x^2}{a^2} − \frac{y^2}{b^2} = 1\) (標準形) |
\(\left\{\begin{array}{l} \displaystyle x = \frac{a}{\cos\theta}\\ y = b\tan\theta\end{array}\right.\) | ||
| サイクロイド | \((x^2 + y^2 − ax)^2 \) \( = a^2(x^2 + y^2)\) | \(\left\{\begin{array}{l} x = a(\theta − \sin\theta)\\ y = a(1 − \cos\theta)\end{array}\right.\) | - | |
| エピサイクロイド | - | \(\left\{\begin{array}{l} \displaystyle x = (a + b)\cos\theta − b\cos\frac{a + b}{b} \theta\\ \displaystyle y = (a + b)\sin\theta − b\sin\frac{a + b}{b} \theta\end{array}\right.\) | - | |
| カージオイド | - | \(\left\{\begin{array}{l} x = a(1 + \cos\theta)\cos\theta\\ y = a(1 + \cos\theta)\sin\theta\end{array}\right.\) | \(r = a(1 + \cos\theta)\) | |
| ハイポサイクロイド | - | \(\left\{\begin{array}{l} \displaystyle x = (a − b)\cos\theta + b\cos\frac{b − a}{b} \theta\\ \displaystyle y = (a − b)\sin\theta + b\sin\frac{b − a}{b} \theta\end{array}\right.\) | - | |
| アステロイド | \(x^{\frac{2}{3}} + y^{\frac{2}{3}} \) \( = a^{\frac{2}{3}}\) | \(\left\{\begin{array}{l} x = a\cos^3\theta\\ y = a\sin^3\theta\end{array}\right.\) | - | |
| リマソン | \((x^2 + y^2 − bx)^2 \) \( = a^2(x^2 + y^2)\) | \(\left\{\begin{array}{l} x = \cos\theta(a + b\cos\theta)\\ y = \sin\theta(a + b\cos\theta)\end{array}\right.\) | \(r = a + b\cos\theta\) | |
| 螺
旋 系 |
アルキメデスの渦巻線 | - | \(\left\{\begin{array}{l} x = a\theta\cos\theta\\ y = a\theta\sin\theta\end{array}\right.\) | \(r = a\theta\) |
| 対数螺旋 | - | \(\left\{\begin{array}{l} x = ae^{b\theta}\cos\theta\\ y = ae^{b\theta}\sin\theta\end{array}\right.\) | \(r = ae^{b\theta}\) | |
| リサージュ曲線 | - | \(\left\{\begin{array}{l} x = A\sin(a\theta+ \delta)\\ y = B\sin b\theta\end{array}\right.\) | - | |
| インボリュート曲線 | - | \(\left\{\begin{array}{l} x = a(\cos\theta + \theta\sin\theta)\\y = a(\sin\theta − \theta\cos\theta) \end{array}\right.\) | - | |
| 正葉曲線(バラ曲線) | - | \(\left\{\begin{array}{l} x = \sin a\theta\cos\theta\\ y = \sin a\theta\sin\theta\end{array}\right.\) | \(r = \sin a\theta\) | |
| レムニスケート | \((x^2 + y^2)^2 \) \( = 2a^2(x^2 − y^2)\) | \(\left\{\begin{array}{l} x = \sqrt{2} a\cos\theta \sqrt{\cos2\theta}\\ y = \sqrt{2} a\sin\theta \sqrt{\cos2\theta}\end{array}\right.\) | \(r^2 = 2a^2\cos2\theta\) | |
媒介変数表示には複数通りありますが、そのうち代表的なものだけを示しています。
なお、極方程式が \(r = f(\theta)\) の形で表せるものは、以下のように簡単に媒介変数表示に変換できます。
極方程式と媒介変数表示の変換
\(r = f(\theta)\) \(\iff x = f(\theta)\cos\theta, y = f(\theta)\sin\theta\)
円錐曲線(二次曲線)
円錐曲線とは、円錐⾯を任意の平⾯で切断したときの断⾯として得られる曲線群です。
切断の仕方によって、円・楕円・放物線・双曲線の \(4\) 種類の曲線があります。
別名、「二次曲線」とも呼ばれます。
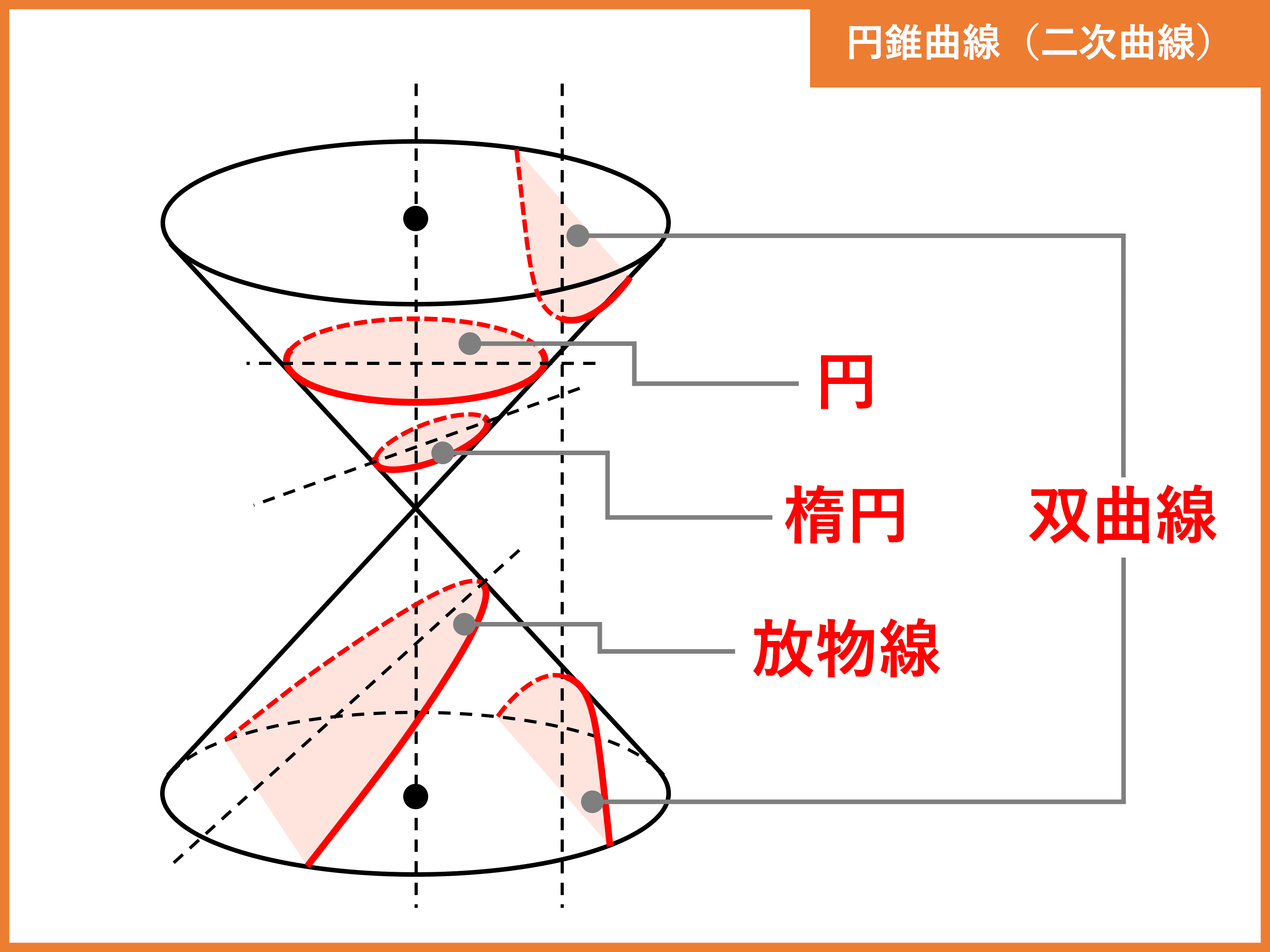
- 円:全ての⺟線と交わり、底⾯に平⾏な平⾯で切断
- 楕円:全ての⺟線と交わり、底⾯に平⾏でない平⾯で切断
- 放物線:⺟線に平⾏な⾯で切断
- 双曲線:⺟線に平⾏でない平⾯で切断
円錐曲線は、「定点 \(\mathrm{F}\) (焦点) と、\(\mathrm{F}\) を通らない定直線 \(\ell\) (準線) からの距離の比が一定である点 \(\mathrm{P}\) の軌跡」と定義できます。

(点 \(\mathrm{P}\) と焦点 \(\mathrm{F}\) の距離) : (点 \(\mathrm{P}\) と準線 \(\ell\) の距離) \(= e : 1\)
としたときの \(e\) を「離心率」と呼び、これを用いるとどの円錐曲線も極方程式 \(\color{red}{\displaystyle r = \frac{l}{1 \pm e\cos\theta}}\)(※) の \(1\) 通りで表せるという特徴があります。

※ 準線 \(\ell\) が焦点 \(\mathrm{F}\) より右にある場合は \(\displaystyle r = \frac{l}{1 + e\cos\theta}\)、左にある場合は \(\displaystyle r = \frac{l}{1 − e\cos\theta}\) となります。
また、円だけは上記の定義に当てはまらないものの、便宜上、円の離心率を \(e = 0\) とおくと都合がよい場合があります。
円
円の定義および式は次の通りです。
定点 \(\mathrm{O}\) (中心) からの距離 \(a\) (半径) が一定となる点の軌跡。
- 方程式(直交座標)
\(x^2 + y^2 = a^2\) - 媒介変数表示
\(\left\{\begin{array}{l} x = a\cos\theta\\ y = a\sin\theta\end{array}\right.\) - 極方程式
\(r = a\)
(ただし、\(a > 0\))

なお、数IIで習う円の方程式の内容は以下の記事にまとめています。
 円の方程式の公式や求め方をわかりやすく解説!円の接線も
円の方程式の公式や求め方をわかりやすく解説!円の接線も
楕円
楕円の定義および式は次の通りです。
\(2\) 定点(焦点)からの距離の和が一定となる点の軌跡。
- 方程式(直交座標)
1. \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((a > b > 0)\) (標準形、焦点が \(x\) 軸上)
2. \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) \((b > a > 0)\) (焦点が \(y\) 軸上)
- 媒介変数表示
\(\left\{\begin{array}{l} x = a\cos\theta\\ y = b\sin\theta\end{array}\right.\) - 極方程式
\(\displaystyle r = \frac{l}{1 \pm e\cos\theta}\) (\(0 < e < 1\))
(ただし、\(a > 0\), \(b > 0\), \(l > 0\))

なお、楕円の方程式の内容は以下の記事にまとめています。
 楕円とは?方程式やグラフ、焦点・接線・面積の求め方
楕円とは?方程式やグラフ、焦点・接線・面積の求め方
放物線
放物線の定義および式は次の通りです。
定点 \(\mathrm{F}\)(焦点)と、\(\mathrm{F}\) を通らない定直線 \(\ell\) からの距離が等しい点の軌跡。
- 方程式(直交座標)
1. \(y^2 = 4px\) (標準形、焦点が \(x\) 軸上)
2. \(x^2 = 4py\) (焦点が \(y\) 軸上) - 媒介変数表示
1. \(\left\{\begin{array}{l} x = pt^2\\ y = 2pt\end{array}\right.\)
2. \(\left\{\begin{array}{l} x = 2pt\\ y = pt^2\end{array}\right.\) - 極方程式
\(\displaystyle r = \frac{l}{1 \pm e\cos\theta}\) \((e = 1)\)
(ただし、\(p \neq 0\), \(l > 0\))

「放物線」という名前自体は、物体を投げたときの軌跡がこの曲線となることに由来しています。
双曲線
双曲線の定義および式は次の通りです。
\(2\) 定点(焦点)からの距離の差が一定となる点の軌跡。
- 方程式(直交座標)
1. \(\displaystyle \frac{x^2}{a^2} − \frac{y^2}{b^2} = 1\) (標準形、焦点が \(x\) 軸上)
2. \(\displaystyle \frac{x^2}{a^2} − \frac{y^2}{b^2} = −1\) (焦点が \(y\) 軸上) - 媒介変数表示
1. \(\left\{\begin{array}{l} \displaystyle x = \frac{a}{\cos\theta}\\ y = b\tan\theta\end{array}\right.\)
2. \(\left\{\begin{array}{l} x = a\tan\theta\\ \displaystyle y = \frac{b}{\cos\theta}\end{array}\right.\) - 極方程式
\(\displaystyle r = \frac{l}{1 \pm e\cos\theta}\) \((1 < e)\)
(ただし、\(a > 0\), \(b > 0\), \(l > 0\))

なお、双曲線の方程式の内容は以下の記事にまとめています。
 双曲線とは?方程式やグラフ、焦点・漸近線・接線の求め方
双曲線とは?方程式やグラフ、焦点・漸近線・接線の求め方
サイクロイド
サイクロイドとは、直線上で円をすべらず転がしたとき、円周上の定点が描く軌跡です。
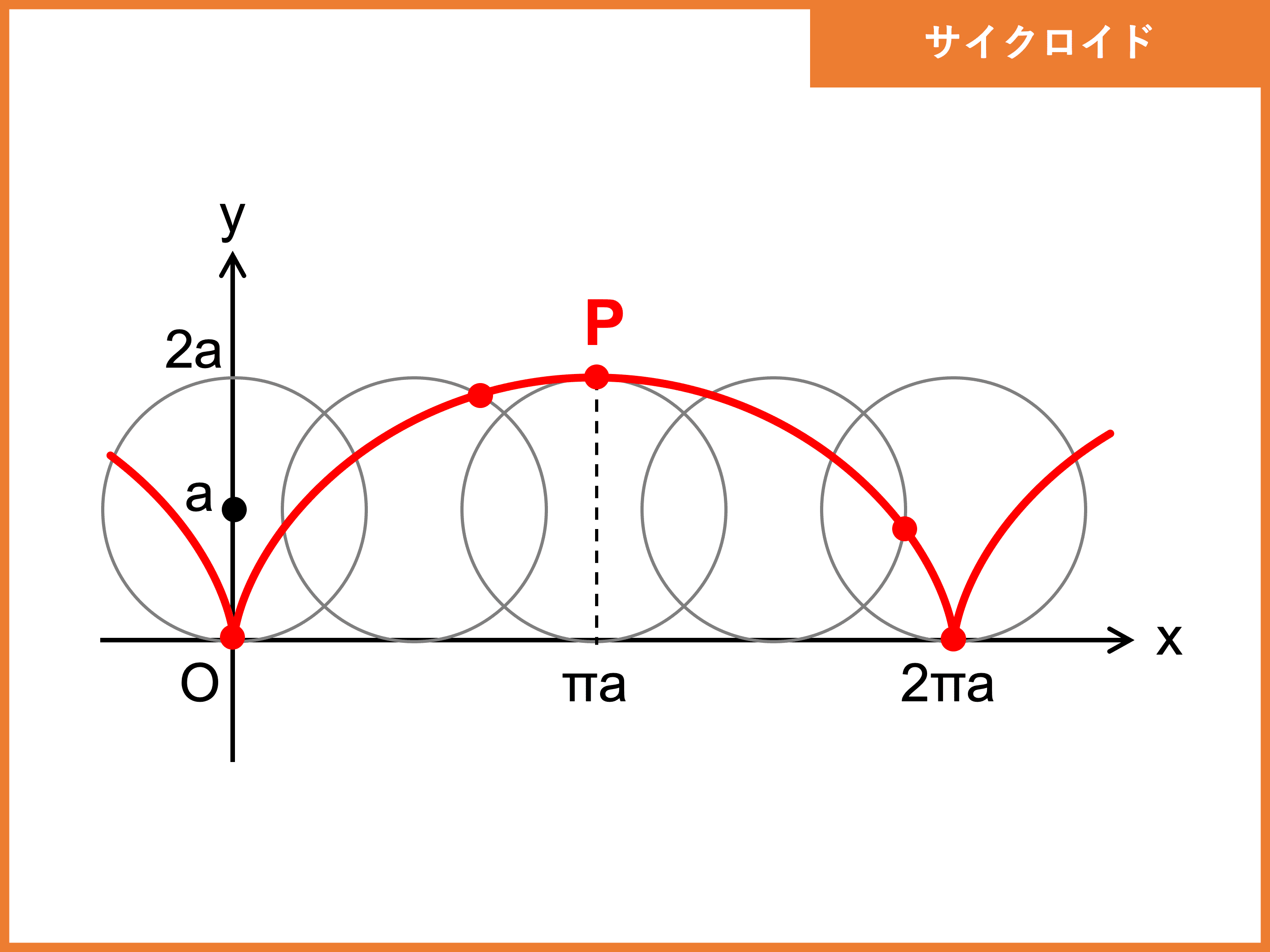
名前は円が回転すること (= cycle) に由来します(cycloid = 円形)。
サイクロイドは、媒介変数表示で表せる曲線の中で特に有名です。
動く円の半径を \(a \,(> 0)\) とおくと、
\begin{align}\left\{\begin{array}{l} x = a(\theta − \sin\theta)\\ y = a(1 − \cos\theta)\end{array}\right.\end{align}

エピサイクロイド(外サイクロイド)
エピサイクロイドとは、定円の外側である円をすべらず転がしたとき、動く円の周上の定点が描く軌跡です。

「エピ (epi−)」は外側を意味しています。
エピサイクロイドは、媒介変数表示で以下のように表せます。
定円の半径を \(a \,(> 0)\)、動く円の半径を \(b \,(> 0)\) とおくと、
\begin{align}\left\{\begin{array}{l} \displaystyle x = (a + b)\cos\theta − b\cos\frac{a + b}{b} \theta\\ \displaystyle y = (a + b)\sin\theta − b\sin\frac{a + b}{b} \theta\end{array}\right.\end{align}

カージオイド(心臓形)
エピサイクロイドのうち、動く円と定円の半径の比が \(1 : 1\) である場合を特に「カージオイド」と呼びます。

名前は心臓に似ていることに由来します(cardioid = 心臓形)。
カージオイドは、媒介変数表示だけでなく極方程式でも簡潔に表せるのが特徴です。
\(a > 0\) のとき、
- 極方程式
\(r = a(1 + \cos\theta)\) - 媒介変数表示
\(\left\{\begin{array}{l} x = a(1 + \cos\theta)\cos\theta\\ y = a(1 + \cos\theta)\sin\theta\end{array}\right.\)
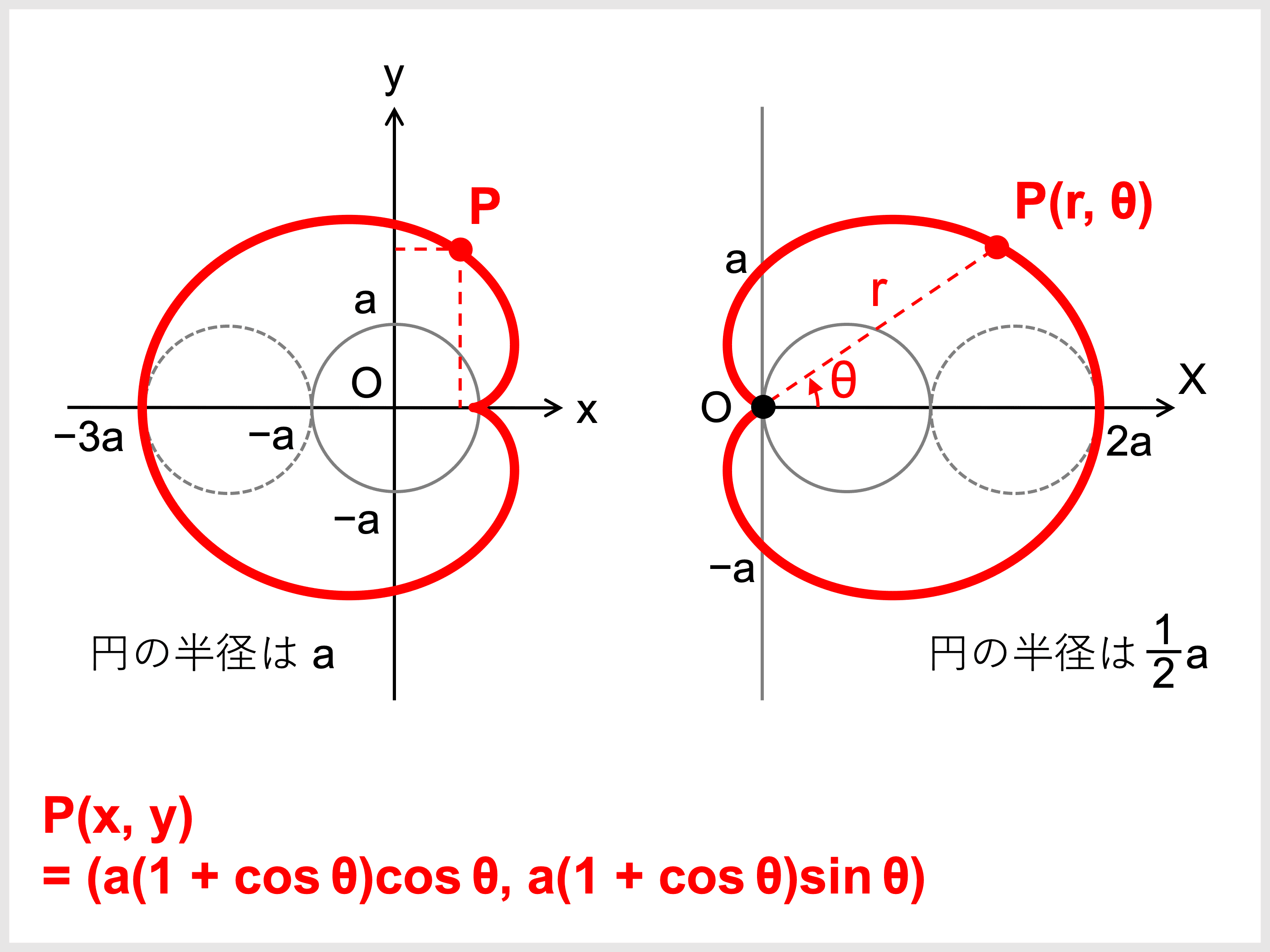
ちなみに、カージオイドは後ほど説明するリマソン(極方程式 : \(r = a + b\cos\theta\))において \(a = b\) とした場合と考えることもできます。
ハイポサイクロイド(内サイクロイド)
ハイポサイクロイドとは、定円の内側である円をすべらず転がしたとき、動く円の周上の定点が描く軌跡です。

「ハイポ (hypo−)」は内側を意味しています。
ハイポサイクロイドは、媒介変数表示で以下のように表せます。
定円の半径を \(a \,(> 0)\)、動く円の半径を \(b \,(> 0)\) とおくと、
\begin{align}\left\{\begin{array}{l} \displaystyle x = (a − b)\cos\theta + b\cos\frac{b − a}{b} \theta\\ \displaystyle y = (a − b)\sin\theta + b\sin\frac{b − a}{b} \theta\end{array}\right.\end{align}

アステロイド(星芒形)
ハイポサイクロイドのうち、動く円と定円の半径の比が \(1 : 4\) である場合を特に「アステロイド」と呼びます。

名前は星の形に似ていることに由来します(astroid = 星芒形)。
アステロイドは、媒介変数表示だけでなく直交座標の方程式でも簡潔に表せます。
定円の半径を \(a \,(> 0)\) とおくと(動く円の半径は \(\displaystyle \frac{a}{4}\))、
- 方程式(直交座標)
\(x^{\frac{2}{3}} + y^{\frac{2}{3}} = a^{\frac{2}{3}}\) - 媒介変数表示
\(\left\{\begin{array}{l} x = a\cos^3\theta\\ y = a\sin^3\theta\end{array}\right.\)

リマソン(パスカルの蝸牛形)
リマソンとは、定円上を動く点 \(\mathrm{A}\) と定点 \(\mathrm{O}\) を結ぶ直線 \(\mathrm{OA}\) 上の点で、\(\mathrm{AP} = \mathrm{AQ}\) である点 \(\mathrm{P}\), \(\mathrm{Q}\) の軌跡です(円の垂足曲線ともいいます)。

名前の由来はカタツムリ(蝸牛、ラテン語で limaçon)です(必ずしもカタツムリの形に似ているわけでもないのですが)。
リマソンは方程式・媒介変数表示・極方程式のどれでも表せますが、極方程式が非常にシンプルです。
定円の直径を \(b \,(> 0)\)、\(\mathrm{AP} = \mathrm{AQ} = a \,(> 0)\) とおくと、
- 極方程式
\(r = a + b\cos\theta\) - 媒介変数表示
\(\left\{\begin{array}{l} x = \cos\theta(a + b\cos\theta)\\ y = \sin\theta(a + b\cos\theta)\end{array}\right.\) - 方程式(直交座標)
\((x^2 + y^2 − bx)^2 = a^2(x^2 + y^2)\)

また、リマソンにおいて、\(a = b\) の場合がカージオイドとなります。
螺旋系
数ある螺旋のうち、\(2\) つだけ紹介します。
アルキメデスの渦巻線(正渦線)
アルキメデスの渦巻線は、渦巻が等間隔になっているのが特徴です。

極方程式で表すと非常に簡潔です。
- 極方程式
\(r = a\theta\) - 媒介変数表示
\(\left\{\begin{array}{l} x = a\theta\cos\theta\\ y = a\theta\sin\theta\end{array}\right.\)
(ただし、定数 \(a > 0\))
対数螺旋(等角螺旋)
対数螺旋は別名「等角螺旋」「ベルヌーイの螺旋」と呼ばれ、⾃然界によく⾒られる螺旋です。
渦巻の間隔は外側に向かって広くなっていきます。

対数螺旋も、極方程式で簡潔に表現できます。
- 極方程式
\(r = ae^{b\theta}\) - 媒介変数表示
\(\left\{\begin{array}{l} x = ae^{b\theta}\cos\theta\\ y = ae^{b\theta}\sin\theta\end{array}\right.\)
(ただし、\(a \,(> 0)\), \(b\) は定数、\(e\) はネイピア数)
定数 \(b\) が正の場合は中心から左曲がり、負の場合は中心から右曲がりの螺旋になります。
その他の曲線
その他、大学入試などでも取り上げられる曲線について説明します(順不同)。
リサージュ曲線
リサージュ曲線は、縦方向・横方向の単振動を合成して得られる曲線です。
単振動の振幅・角周波数・位相差によってさまざまな形をとります。
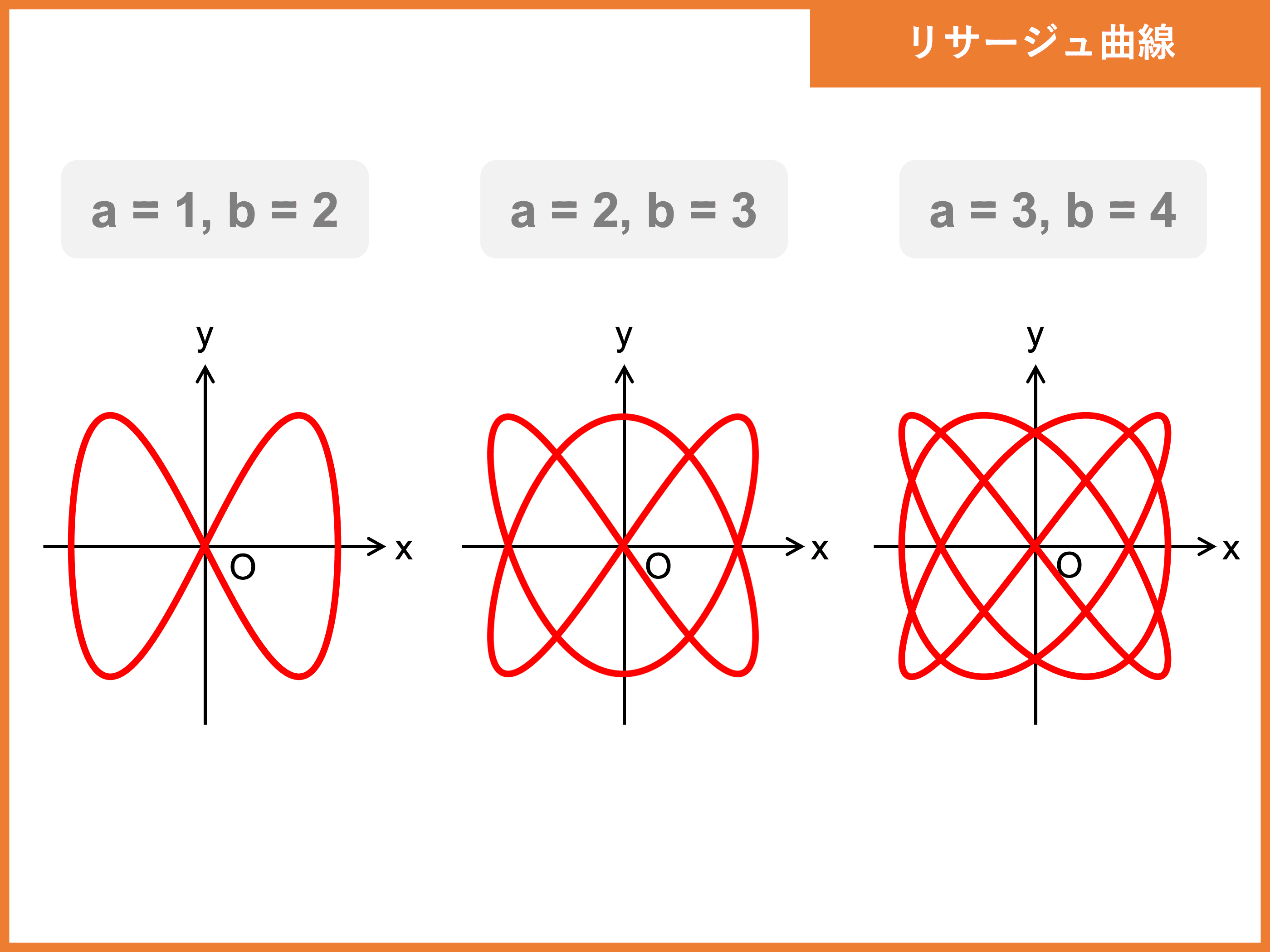
周波数の測定に用いられることが多く、オシロスコープで実際に観測することもできます。
リサージュ曲線は、媒介変数表示で以下のように表せます。
\begin{align}\left\{\begin{array}{l} x = A\sin(a\theta+ \delta)\\ y = B\sin b\theta\end{array}\right.\end{align}
-
- 振幅 : \(A, B > 0\)
- 角周波数 : \(a, b\)
- 位相差 : \(\delta\)
インボリュート曲線
インボリュート曲線は、固定したリール(糸巻き)から糸がたるまないようにほどくときに糸の端点が描く軌跡です。
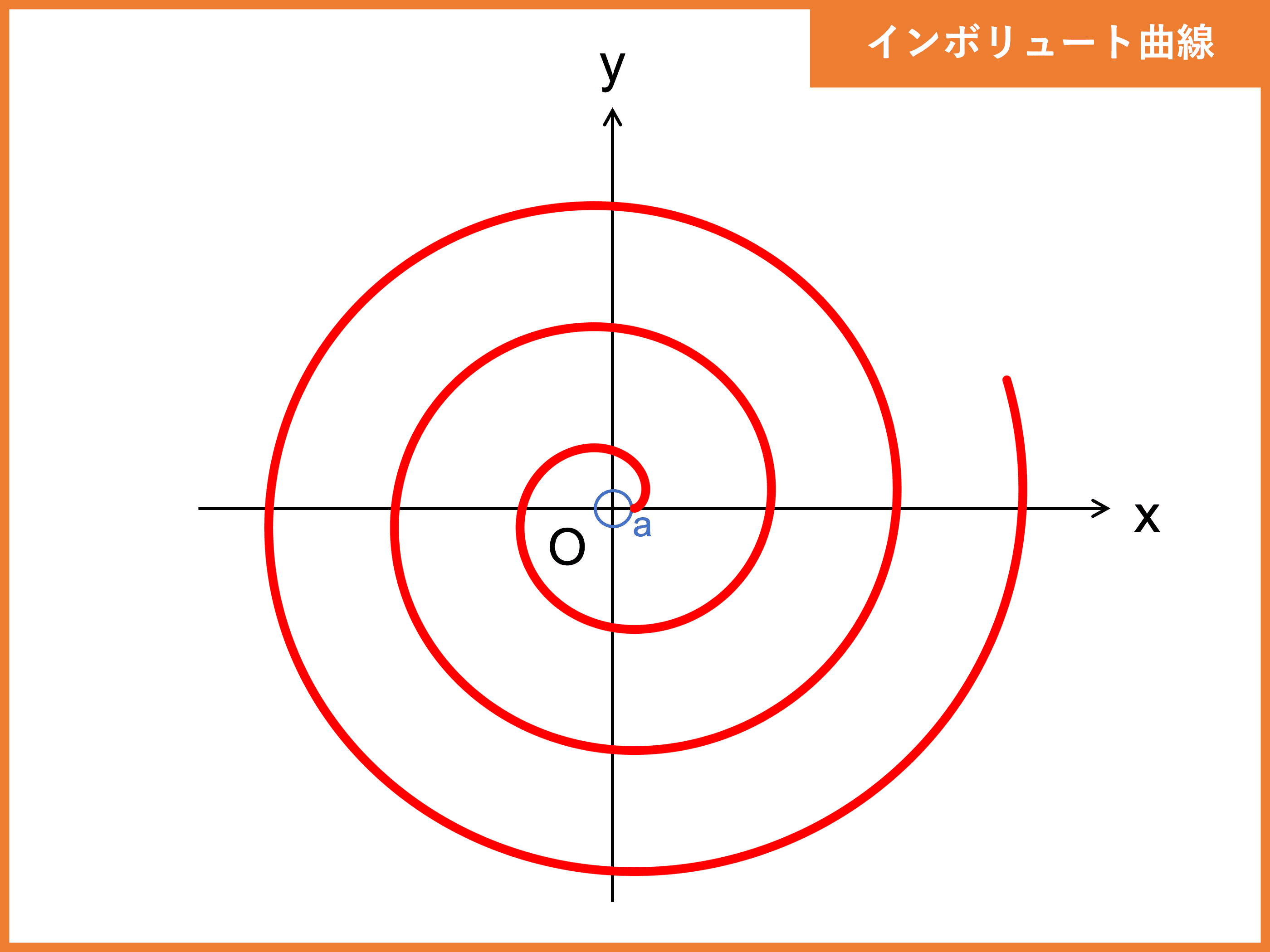
媒介変数表示で以下のように表せます。
リール (中心円) の半径を \(a \,(> 0)\) とすると、
\begin{align}\left\{\begin{array}{l} x = a(\cos\theta + \theta\sin\theta)\\ y = a(\sin\theta − \theta\cos\theta)\end{array}\right.\end{align}
正葉曲線(バラ曲線)
正葉曲線(バラ曲線)は、バラに似た形となることから名付けられた曲線で、媒介変数表示および極方程式で表せます。
- 極方程式
\(r = \sin a\theta\) - 媒介変数表示
\(\left\{\begin{array}{l} x = \sin a\theta\cos\theta\\ y = \sin a\theta\sin\theta\end{array}\right.\)
(ただし、定数 \(a\) は有理数)
定数 \(a\) の値は、ループの数と形状に関わります。
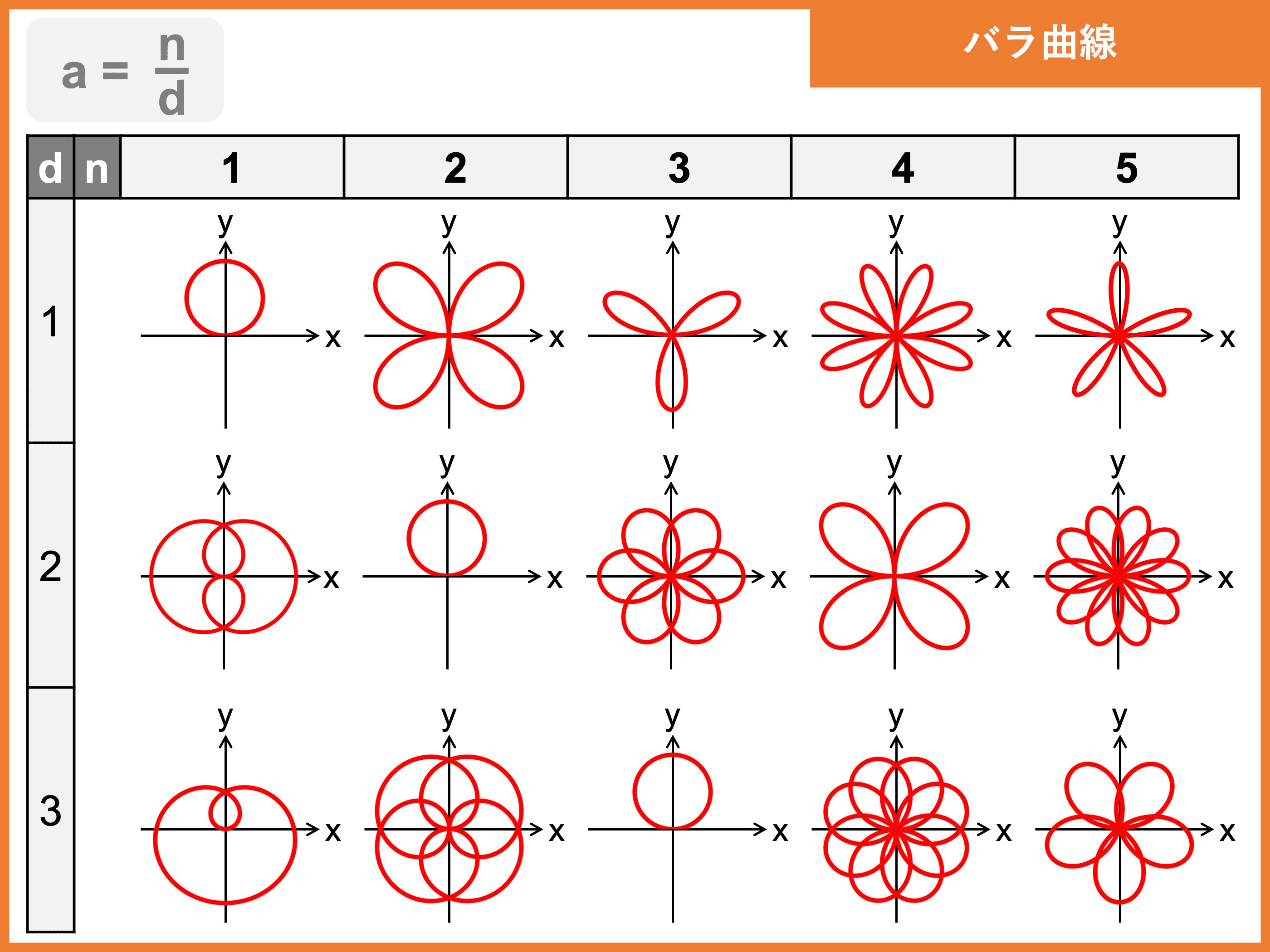
\(a\) が偶数の場合はループが \(2a\) 個、奇数の場合はループが \(a\) 個になります。
また、\(a\) が整数でない場合はループの形状が少し複雑になります。
レムニスケート(連珠形)
レムニスケートとは、\(2\) 定点(焦点)からの距離の積が一定な点の軌跡です。

レムニスケートは方程式・媒介変数表示・極方程式のどれでも表せますが、極方程式が最もシンプルです。
原点と焦点の距離を \(a \,(> 0)\) とおくと、
- 極方程式
\(r^2 = 2a^2\cos2\theta\) - 媒介変数表示
\(\left\{\begin{array}{l} x = \sqrt{2}a\cos\theta\sqrt{\cos2\theta}\\ y = \sqrt{2}a\sin\theta\sqrt{\cos2\theta}\end{array}\right.\) - 方程式(直交座標)
\((x^2 + y^2)^2 = 2a^2(x^2 − y^2)\)
レムニスケートは、直角双曲線の垂足曲線でもあります。
よく見ると定義も双曲線に似ていますね。

以上で解説は終わりです。
式と曲線を習っているとバラバラに登場して関連性がつかみにくい曲線たちですが、この記事が理解の助けになれば幸いです!




放物線の一種になると思われますが、「さち曲線」と呼ばれる曲線について、求め方を示していただきたいと思います。
例えば、給料について、初任給をいくらにして徐々に昇給していくけれど最終的にある額以上にはならない。という曲線をイメージしています。
コメントありがとうございます。
当サイトでは、「高校教科書レベルの知識をわかりやすく説明すること」をモットーにしていますので、その範疇を超える概念についてはご要望に添うことができません。
今後ともどうぞ当サイトをよろしくお願いいたします。
バラ曲線がよかったです特に
この度はコメントいただきありがとうございます。
見やすい・わかりやすい図になっていればこちらもうれしいです!