この記事では「三次方程式」について、因数分解の公式や因数定理を利用する解き方を解説していきます。
また、三次方程式の解と係数の関係や、解の公式、判別式とグラフの関係なども説明していくので、ぜひこの記事を通してマスターしてくださいね!
目次
三次方程式とは?
三次方程式とは、三次式を含む方程式です。
三次方程式の一般形は \(\color{red}{ax^3 + bx^2 + cx + d = 0}\) (\(a, b, c, d\) は定数、\(a \neq 0\))と表すことができます。
三次方程式の解
一般に、係数が実数である三次方程式は次の \(3\) 解をもちます。
- \(3\) つの異なる実数解
- \(3\) つの実数解のうち、少なくとも \(1\) 組が重解
- \(1\) つの実数解と \(2\) つの虚数解
学校では、三次方程式の前に複素数(虚数を含む数体系)を習うので、虚数解も解に含めることが一般的です。
三次方程式の解き方
三次方程式を解くためには、基本的に因数分解が必要となります。
この因数分解のやり方には、次の \(2\) 通りの方法があります。
- 三次式の因数分解の公式を利用する
- 因数定理を利用する
それぞれ、順番に紹介していきます。
解き方① 三次式の因数分解の公式を使う
三次式の因数分解の公式を利用して三次方程式を因数分解する方法を説明します。
\(x^3 − 8 = 0\) を解きなさい。
右辺に何か数値がある場合は、すべて左辺に移項して \((左辺) = 0\) の形にします。
この問題ではすでに \(x^3 − 8 = 0\) となっていますね。
三次方程式を解く問題では、左辺に注目して、三次式の因数分解の公式に当てはまるかどうかを確認します。
三次式の因数分解の公式
- \(a^3 + b^3 = (a + b)(a^2 − ab + b^2)\)
- \(a^3 − b^3 = (a − b)(a^2 + ab + b^2)\)
- \(a^3 + 3a^2b + 3ab^2 + b^3 = (a + b)^3\)
- \(a^3 − 3a^2b + 3ab^2 − b^3 = (a − b)^3\)
この問題の左辺 \(x^3 − 8\) は \(a^3 − b^3\) の形をしているので、上から \(2\) 番目の公式を使って因数分解できそうですね。
STEP.2 で特定した公式に沿って左辺を因数分解します。
この問題では公式 \(a^3 − b^3 = (a − b)(a^2 + ab + b^2)\) ですね。
\(\begin{align}x^3 − 8 &= x^3 − 2^3\\&= (x − 2)(x^2 + 2x + 2^2)\\&= (x − 2)(x^2 + 2x + 4)\end{align}\)
因数分解された \((左辺) = 0\) を解くと、解の \(1\) つが求められます。
\((x − 2)(x^2 + 2x + 4) = 0\) より、
\(x = \color{red}{2}\), \(x^2 + 2x + 4 = 0\)
なお、公式 \(a^3 \pm 3a^2b + 3ab^2 \pm b^3 = (a \pm b)^3\) を使うパターンでは、ここまでで解がすべて求められます(重解)。
三次方程式を因数分解して新たに得られた二次方程式を解きます。
\(x^2 + 2x + 4 = 0\) は直接因数分解できなそうなので、二次方程式の解の公式を利用します。
(二次方程式の)解の公式
二次方程式 \(ax^2 + bx + c = 0\) の解 \(x\) は
\(\begin{align}x = \displaystyle \frac{− b \pm \sqrt{b^2 − 4ac}}{2a}\end{align}\)
\(x^2 + 2x + 4 = 0\) について、解の公式より
\(\begin{align} x &= \frac{−1 \pm \sqrt{1 − 1 \cdot 4}}{1} \\ &= −1 \pm \sqrt{1 − 4} \\ &= − 1 \pm \sqrt{−3} \\ &= \color{red}{−1 \pm \sqrt{3} i} \end{align}\)
答え: \(\color{red}{x = 2, −1 \pm \sqrt{3} i}\)
これで、三次方程式 \(x^3 − 8 = 0\) の \(3\) 解が求められましたね(\(1\) つの実数解と \(2\) つの虚数解)。
解き方② 因数定理を使う
因数定理を利用して三次方程式を因数分解する方法を説明します。
\(x^3 − x^2 − 4x + 4 = 0\) を解きなさい。
定数項が \(+4\) のため何かの \(3\) 乗とは考えにくく、因数分解の公式には当てはまらなそうです。
このように三次式の因数分解の公式に当てはまらない問題でも、因数定理を使えば因数を見つけることができます。
因数定理
整式 \(P(x)\) が \((x − a)\) を因数にもつ \(\iff P(a) = 0\)
因数定理を利用する準備として、\(P(x) = (左辺)\) とおきます。
\(P(x) = x^3 − x^2 − 4x + 4\) とおく。
因数定理から、\(P(a) = 0\) になる \(a\) の値を見つければ、\(P(x)\) が \((x − a)\) を因数にもつことがわかります。
\(x\) に適当な値を代入して答えが \(0\) になるものを見つけましょう。
\(P(x) = x^3 − x^2 − 4x + 4\) において、
\(\begin{align} P(1) &= 1^3 − 1^2 − 4 \cdot 1 + 4 \\ &= 1 − 1 − 4 + 4 \\ &= 0 \end{align}\)
よって、\(P(x)\) は \((x − 1)\) を因数にもつことがわかりました。
見つけた因数で \(P(x)\) を割り算します。
割り算の結果、商の二次式がさらに因数分解できれば因数分解します。
\(P(x)\) を \((x − 1)\) でくくると、
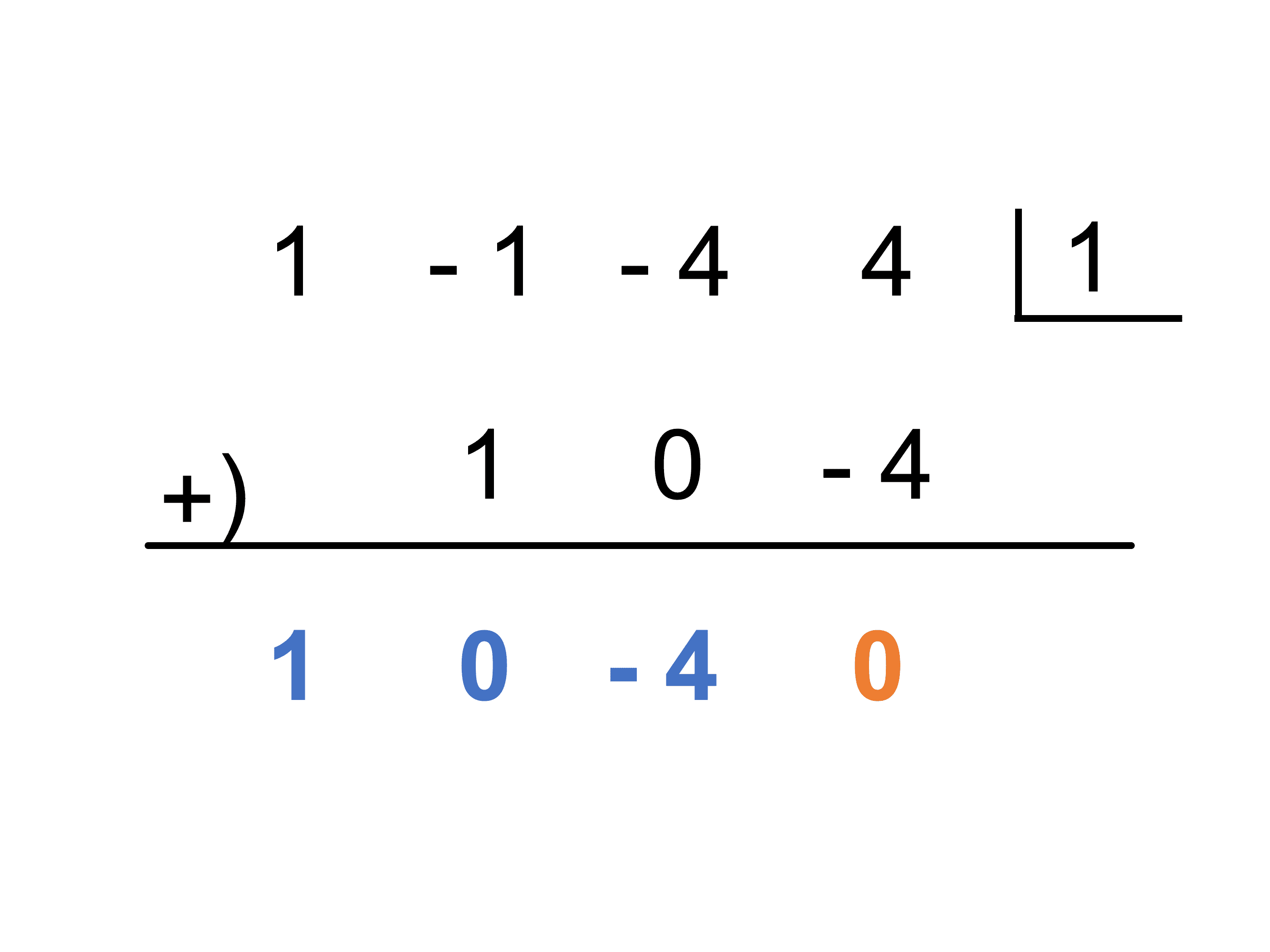
\(\begin{align} P(x) &= (x − 1)(x^2 − 4) \\ &= (x − 1)(x + 2)(x − 2) \end{align}\)
\((x − 1)(x + 2)(x − 2) = 0\) より
\(x = −2, 1, 2\)
答え: \(\color{red}{x = −2, 1, 2}\)
このように、答えが求められました!(\(3\) つの異なる実数解)
STEP.2 で因数を見つけるコツなど、因数定理の詳しい使い方を説明しています。
 因数定理とは?使い方や因数の見つけ方をわかりやすく解説!
因数定理とは?使い方や因数の見つけ方をわかりやすく解説!
また、STEP. 3 の割り算では「組立除法」を利用しています。
 組立除法とは?やり方や原理をわかりやすく解説!
組立除法とは?やり方や原理をわかりやすく解説!
三次方程式の解と係数の関係
三次方程式の解と係数との間には、以下の関係が成り立ちます。
三次方程式 \(ax^3 + bx^2 + cx + d = 0\) \((a \neq 0)\) の \(3\) つの解が \(\alpha\), \(\beta\), \(\gamma\) であるとき、以下が成り立つ。
\begin{align}\color{red}{\left\{\begin{array}{l} \displaystyle \alpha + \beta + \gamma = −\frac{b}{a}\\ \displaystyle \alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}\\ \displaystyle \alpha\beta\gamma = −\frac{d}{a}\end{array}\right.}\end{align}
\(3\) 解の和、\(2\) 解の積の和、\(3\) 解の積は、三次方程式の係数を使って計算できるのですね。
「解と係数の関係」がなぜ成り立つのかは、以下の記事で詳しく説明しています。
 解と係数の関係とは?公式やその逆、証明、応用問題
解と係数の関係とは?公式やその逆、証明、応用問題
例題「三次方程式の解と係数の関係の使い方」
以下の例題で、三次方程式における解と係数の関係の使い方を説明します。
\(2x^3 + 3x^2 + 4x + 5 = 0\) の \(3\) つの解を \(\alpha\), \(\beta\), \(\gamma\) とする。
このとき、\(\alpha^2 + \beta^2 + \gamma^2\) の値を求めなさい。
三次方程式を解いて \(\alpha\), \(\beta\), \(\gamma\) を求めてから\(\alpha^2 + \beta^2 + \gamma^2\) の値を求めるのは少し手間がかかります。
そこで解と係数の関係を利用すると、\(\alpha\), \(\beta\), \(\gamma\) を直接求めなくてもよいという利点があります。
まずは、値を求めたい式 \(\alpha^2 + \beta^2 + \gamma^2\) を \(\alpha + \beta + \gamma\), \(\alpha\beta + \beta\gamma + \gamma\alpha\), \(\alpha\beta\gamma\) のいずれかだけで表せるように変形します。
\(\alpha^2 + \beta^2 + \gamma^2\) はすべての項が二次式なので、\((\alpha + \beta + \gamma)^2\) を展開してみるとうまくいきます。
\((\alpha + \beta + \gamma)^2 \\ = \alpha^2 + \beta^2 + \gamma^2 + 2\alpha\beta + 2\beta\gamma + 2\gamma\alpha\)
より、
\(\alpha^2 + \beta^2 + \gamma^2\)
\(=(\alpha + \beta + \gamma)^2 − 2(\alpha\beta + \beta\gamma + \gamma\alpha)\) …(*)
\(\alpha^2 + \beta^2 + \gamma^2\) は、\(\alpha + \beta + \gamma\) と \(\alpha\beta + \beta\gamma + \gamma\alpha\) だけで表せるようですね。
ここで、解と係数の関係を利用して \(\alpha + \beta + \gamma\) と \(\alpha\beta + \beta\gamma + \gamma\alpha\) の値を求めます。
\(\begin{align}\left\{\begin{array}{l} \displaystyle \alpha + \beta + \gamma = −\frac{b}{a}\\ \displaystyle \alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}\\ \displaystyle \alpha\beta\gamma = −\frac{d}{a}\end{array}\right.\end{align}\) でしたね。
\(2x^3 + 3x^2 + 4x + 5 = 0\) において、
解と係数の関係より
\(\displaystyle \alpha + \beta + \gamma = −\frac{3}{2}\)
\(\displaystyle \alpha\beta + \beta\gamma + \gamma\alpha = \frac{4}{2} = 2\)
あとは、それらをSTEP.1 の式 (*) に代入するだけです。
(*) に代入して
\(\alpha^2 + \beta^2 + \gamma^2\)
\(= (\alpha + \beta + \gamma)^2 − 2(\alpha\beta + \beta\gamma +\gamma\alpha)\)
\(\displaystyle = \left(−\frac{3}{2} \right)^2 − 2 \cdot 2\)
\(\displaystyle = \frac{9}{4} − 4\)
\(\displaystyle = −\frac{7}{4}\)
答え: \(\color{red}{\displaystyle −\frac{7}{4}}\)
このように、解と係数の関係の公式さえ覚えておけば、面倒な因数分解やべき乗の計算を避けて、簡単な代入計算だけで目的の値を求められますね。
三次方程式の計算問題
それでは、三次方程式の計算問題を解いていきましょう。
計算問題①「三次方程式を解く」
\(8x^3 − 12x^2 + 6x − 1 = 0\) を解きなさい。

まずは、三次式の因数分解の公式が使えないか確認します。
\(8x^3 − 12x^2 + 6x − 1 = 0\)
\((2x)^3 − 3(2x)^2 \cdot 1 + 3(2x) \cdot 1^2 − 1^3 = 0\)
\((2x − 1)^3 = 0\)
よって、\(\displaystyle x = \frac{1}{2}\)
答え: \(\color{red}{\displaystyle \frac{1}{2}}\)
計算問題②「三次方程式を解く 2 」
\(x^3 − 3x^2 − 6x + 8 = 0\) を解きなさい。

三次式の因数分解の公式が使えるか考えてみた結果、使えなさそうな場合は因数定理を使ってみましょう。
\(f(x) = x^3 − 3x^2 − 6x + 8\) とおくと、
\(\begin{align} f(1) &= 1^3 − 3 \cdot 1^2 − 6 \cdot 1 + 8 \\ &= 1 − 3 − 6 + 8 \\ &= 0 \end{align}\)
因数定理より、\(f(x)\) は \((x − 1)\) を因数にもつので、
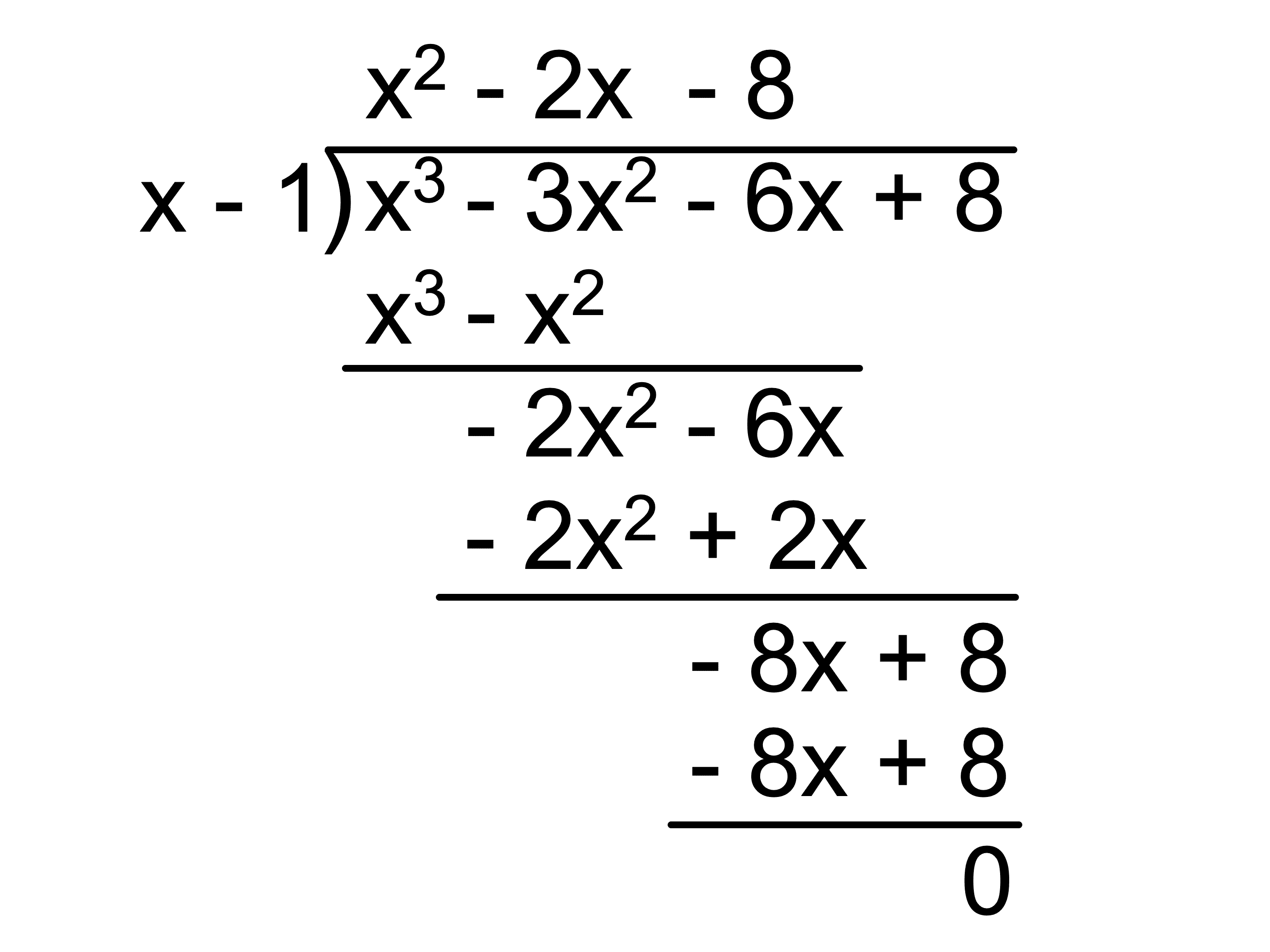
\(\begin{align} f(x) &= (x − 1)(x^2 − 2x − 8) \\ &= (x − 1)(x + 2)(x − 4) \end{align}\)
したがって、
\((x − 1)(x + 2)(x − 4) = 0\)
であるから
\(x = −2, 1, 4\)
答え: \(\color{red}{x = −2, 1, 4}\)
計算問題③「3 解を含む値を求める」
\(3x^3 − 7x + 2 = 0\) の \(3\) つの解を \(\alpha\), \(\beta\), \(\gamma\) とする。
このとき、以下の値を求めなさい。
(1) \(\alpha^2 + \beta^2 + \gamma^2\)
(2) \((\alpha − 1)(\beta − 1)(\gamma − 1)\)
(3) \((\alpha + \beta)(\beta + \gamma)(\gamma + \alpha)\)

解と係数の関係を利用します。
そのために、求めたい式をうまく変形してみましょう。
解と係数の関係より、
\(\left\{\begin{array}{l} \displaystyle \alpha + \beta + \gamma = −\frac{0}{3} = 0 \\ \displaystyle \alpha\beta + \beta\gamma + \gamma\alpha = −\frac{7}{3}\\ \displaystyle \alpha\beta\gamma = −\frac{2}{3}\end{array}\right.\)
(1)
\(\alpha^2 + \beta^2 + \gamma^2\)
\(= (\alpha + \beta + \gamma)^2 − 2(\alpha\beta + \beta\gamma +\gamma\alpha)\)
\(\displaystyle = 0^2 − 2 \cdot \left( −\frac{7}{3} \right)\)
\(\displaystyle = \frac{14}{3}\)
答え: \(\color{red}{\displaystyle \frac{14}{3}}\)
(2)
(見切れる場合は横へスクロール)
与式を展開して整理すると、
\((\alpha − 1)(\beta − 1)(\gamma − 1)\)
\(= (\alpha\beta − \beta − \alpha + 1)(\gamma − 1)\)
\(= \alpha\beta\gamma − \beta\gamma − \gamma\alpha + \gamma − \alpha\beta + \beta + \alpha − 1\)
\(= \alpha\beta\gamma − (\alpha\beta + \beta\gamma +\gamma\alpha) + (\alpha + \beta + \gamma) − 1\)
\(\displaystyle = −\frac{2}{3} − \left(−\frac{7}{3}\right) + 0 − 1\)
\(\displaystyle = \frac{2}{3}\)
答え: \(\color{red}{\displaystyle \frac{2}{3}}\)
(3)
\(\alpha + \beta + \gamma = 0\) より、
\(\left\{\begin{array}{l}\alpha + \beta = −\gamma\\\beta + \gamma = −\alpha\\\gamma + \alpha = −\beta\end{array}\right.\)
なので、与式は
\((\alpha + \beta)(\beta + \gamma)(\gamma + \alpha)\)
\(= (−\gamma)(−\alpha)(−\beta)\)
\(= −\alpha\beta\gamma\)
\(\displaystyle = \frac{2}{3}\)
答え: \(\color{red}{\displaystyle \frac{2}{3}}\)
【参考】三次方程式の解の公式
二次方程式に解の公式があるように、実は三次方程式にも解の公式があります。
しかし、とても長くて複雑です。
複雑すぎて実用的ではないので、利用する必要も覚える必要もありません。
三次方程式 \(ax^3 + bx^2 + cx + d = 0\) \((a ≠ 0)\) の \(3\) つの解を \(\alpha\), \(\beta\), \(\gamma\) とすると
\begin{align}\color{red}{\left\{\begin{array}{l} \alpha = S + T − \displaystyle \frac{b}{3a}\\ \beta = − \displaystyle \frac{S + T}{2} − \frac{b}{3a} + \frac{\sqrt{3}i}{2}(S − T)\\ \gamma = − \displaystyle \frac{S + T}{2} − \frac{b}{3a} − \frac{\sqrt{3}i}{2}(S − T)\end{array}\right.}\end{align}
ただし、
\begin{align}\color{red}{\left\{\begin{array}{l} S = \sqrt[3]{R + \sqrt{Q^3 + R^2}}\\ T = \sqrt[3]{R − \sqrt{Q^3 + R^2}}\end{array}\right.}\end{align}
\begin{align}\color{red}{\left\{\begin{array}{l} Q = \displaystyle \frac{3ac − b^2}{9a^2}\\ R = \displaystyle \frac{9abc − 27a^2d − 2b^3}{54a^3}\end{array}\right.}\end{align}
この公式は別名「カルダノの公式」と呼ばれています。
文字を置き換えず、元の係数 \(a\), \(b\), \(c\), \(d\) で表すと余計に複雑な式になってしまいますね。
【参考】三次方程式の判別式
最後に、三次方程式の判別式について参考程度に説明していきます。
三次方程式 \(ax^3 + bx^2 + cx + d = 0\) \((a ≠ 0)\) の \(3\) つの解を \(\alpha\), \(\beta\), \(\gamma\) とすると、判別式 \(D\) は以下のように表される。
\begin{align}\color{red}{D = a^4(\alpha − \beta)^2(\beta − \gamma)^2(\gamma − \alpha)^2}\end{align}
また、係数のみで判別式を表すと、
\begin{align}\color{red}{D = −4ac^3 − 27a^2d^2 + b^2c^2 + 18abcd − 4b^3d}\end{align}
(見切れる場合は横へスクロール)
\(D\) の値の範囲と解の個数の関係は、
- \(D > 0\) のとき
異なる \(3\) つの実数解をもつ - \(D = 0\) のとき
\(3\) つの実数解のうち、少なくとも \(1\) 組の重解をもつ - \(D < 0\) のとき
\(1\) つの実数解と \(2\) つの虚数解をもつ
解がわかっていれば判別式を使う必要があまりないので、使うとすれば \(2\) つ目の係数で表した式です。
しかし、この複雑な判別式を利用することはオススメしません。
覚えにくいのはもちろん、学校では習わないからです。
三次方程式の解の個数の求め方
三次方程式の解の個数や存在範囲を求める問題では、判別式の代わりにグラフと \(x\) 軸の共有点の個数の関係に落とし込みましょう。
三次方程式 \(ax^3 + bx^2 + cx + d = 0\) の実数解の個数は、三次関数 \(y = ax^3 + bx^2 + cx + d\) と \(x\) 軸 \((y = 0)\) との共有点の個数に等しい。
したがって、「\(y = (\text{三次方程式の左辺})\)」のグラフを書いて、\(x\) 軸との交点の数を求めればよいことになります。
「三次関数のグラフの書き方」については、以下の記事で説明しています。
 三次関数とは?グラフの書き方、極値や接線の求め方(微分)
三次関数とは?グラフの書き方、極値や接線の求め方(微分)
以上で解説は終わりです!
三次方程式について理解が深まりましたか?
因数分解の公式を忘れていた人は、この機会に覚え直しておきましょう。
解き方のパターンを押さえれば、どんな問題でも解けるようになりますよ!



