この記事では、「指数関数」とは何かをわかりやすく解説していきます。
指数関数のグラフや計算問題、指数方程式・指数不等式、指数関数の微分積分の公式なども説明していきますので、ぜひこの記事を通してマスターしてくださいね。
目次
指数関数とは?
指数関数とは、指数部分に変数を含む関数のことです。
\(a > 0, a \neq 1\) のとき、\(a\) を底とする \(x\) の指数関数は
\begin{align}\color{red}{y = a^x}\end{align}
指数関数を定義するとき、底 \(a\) には \(a > 0, a \neq 1\) という条件が必ずつきます。
「底の条件」については、以下の記事で詳しく説明しています。
 真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
真数条件・底の条件とは?なぜ必要かをわかりやすく解説!
指数関数のグラフ
指数関数 \(y = a^x\) のグラフは次のようになります。
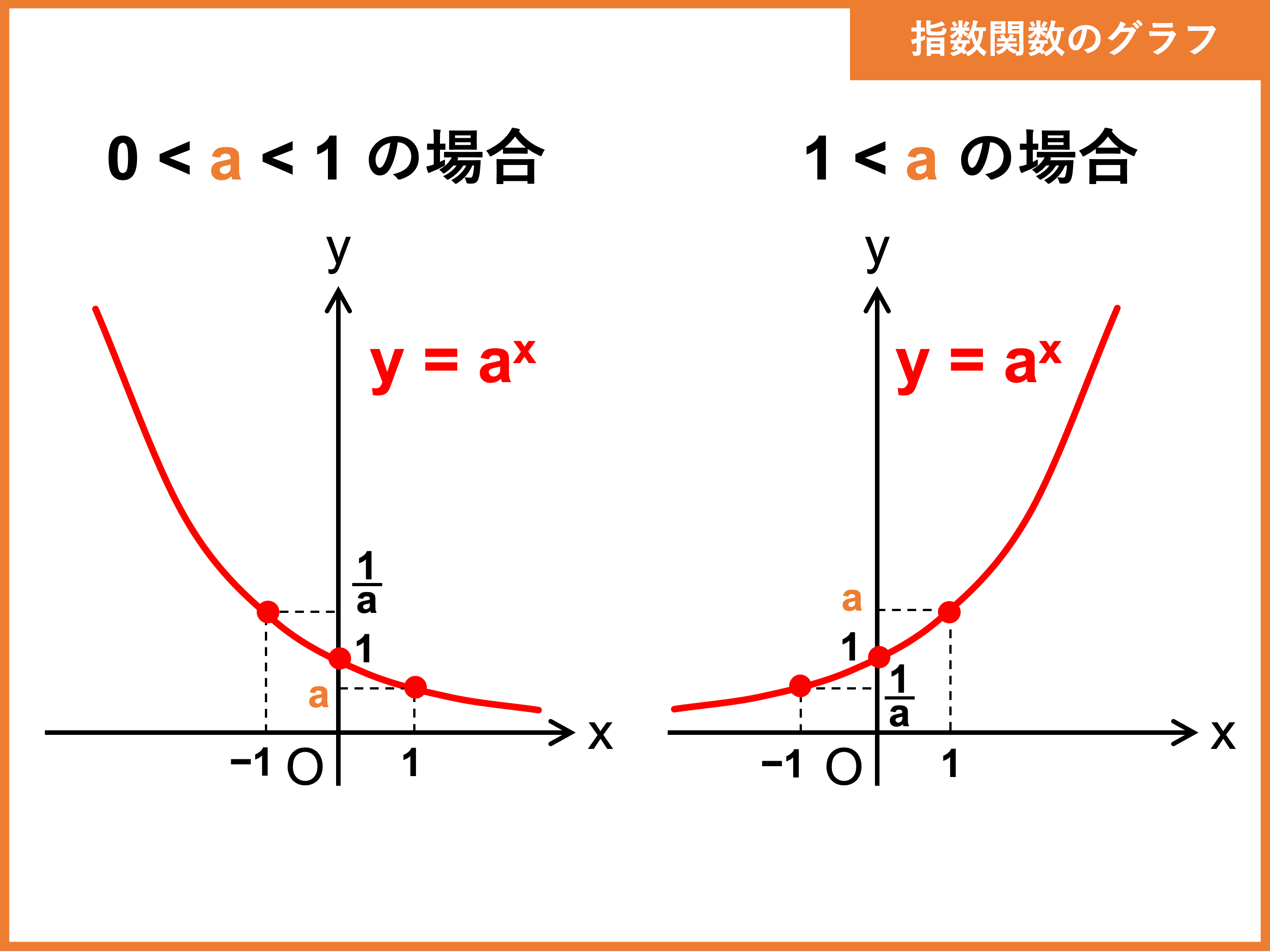
底 \(1 < a\) のときは右肩上がりの曲線、底 \(0 < a < 1\) のときは右肩下がりの曲線です。
このような増加の仕方を指して、「指数関数的な増加」と表現することがありますね。
また、底 \(a > 1\) のときは底が大きいほど、底 \(0 < a < 1\) のときは底が小さいほど指数関数の傾きが急激に増加します。

指数関数の性質
指数関数には、次のような性質があります。
- 定義域は実数全体、値域は正の数全体 \((y > 0)\)
- グラフは必ず点 \((0, 1), (1, a)\) を通る
- \(x\) 軸を漸近線とする
- 底 \(a\) の範囲によって、グラフの増加傾向が異なる
-
- \(1 < a\) のとき
単調増加関数となる(\(x\) の値が増加すれば \(y\) の値も増加)
\begin{align}\color{red}{p < q \iff a^p < a^q}\end{align} - \(0 < a < 1\) のとき
単調減少関数となる(\(x\) の値が増加すれば \(y\) の値は減少)
\begin{align}\color{red}{p < q \iff a^p > a^q}\end{align}
(なお、\(a > 0, a \neq 1\) で「\(p = q \iff a^p = a^q\)」が成り立つ)
- \(1 < a\) のとき
どれも大切な性質なので、グラフと見比べながら確認してくださいね。
指数関数の計算公式
指数関数や指数を含む方程式・不等式の問題を解くには、「指数法則」と「累乗根」の公式を押さえておきましょう。
指数法則
\(a \neq 0\), \(b \neq 0\) で、\(r\), \(s\) が実数、\(m\), \(n\) が正の整数のとき、
- \(\color{red}{a^r \times a^s = a^{r + s}}\)
- \(\color{red}{\displaystyle \frac{a^r}{a^s} = a^{r − s}}\)
- \(\color{red}{(a^r)^s = a^{rs}}\)
- \(\color{red}{(ab)^r = a^r b^r}\)
- \(\color{red}{\displaystyle \left( \frac{b}{a} \right)^r = \frac{b^r}{a^r}}\)
- \(\color{red}{a^0 = 1}\)
- \(\color{red}{\displaystyle a^{−r} = \frac{1}{a^r}}\)
- \(\color{red}{\displaystyle a^{\frac{m}{n}} = \sqrt[n]{a^m}}\)
はじめて指数法則を習ったときは、指数部分が正の整数(自然数)\(m\), \(n\) の場合と習いましたね。
実は、数の範囲を拡張して、指数部分を実数全体としても指数法則は成り立ちます。
だから、指数関数 \(f(x) = a^x\) において \(x\) がどんな実数の値をとっても、関数 \(f\) は連続であるといえるのですね。
累乗根
指数法則の \(\displaystyle a^{\frac{m}{n}} = \sqrt[n]{a^m}\) で示すように、有理数の指数は「累乗根」と捉えることができます。
指数と累乗根の変換はよく行うため、累乗根の性質も理解しておきましょう。
\(a > 0\), \(b > 0\) で、\(m\), \(n\), \(p\) が正の整数のとき \((\sqrt[n]{a})^n = a\), \(\sqrt[n]{a} > 0\) であることから、次の性質が成り立つ。
- \(\color{red}{\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}}\)
- \(\color{red}{\displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\displaystyle \frac{a}{b}}}\)
- \(\color{red}{(\sqrt[n]{a})^m = \sqrt[n]{a^m}}\)
- \(\color{red}{\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}}\)
- \(\color{red}{\sqrt[n]{a^m} = \sqrt[np]{a^{mp}}}\)
累乗根
\(\sqrt[n]{A}\):\(n\) 乗すると \(A\) になる数。
指数関数の計算問題
指数関数のグラフや性質に関する知識を使う計算問題に挑戦しましょう。
計算問題①「指数関数の平行移動とグラフ」
\(y = 3^{x − 1} + 2\) のグラフは、\(y = 3^x\) のグラフを \(x\) 軸方向、\(y\) 軸方向にどれだけ平行移動したグラフであるか。
また、グラフの概形を書け。

グラフの平行移動の考え方は、指数関数であっても同じです。
グラフの平行移動
\(y = f(x)\) を \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\) だけ平行移動した関数は
\begin{align}y − q = f(x − p)\end{align}
指数関数のグラフを書く際は漸近線に注意しましょう。\(y = a^x\) の場合は \(x\) 軸(\(y = 0\))が漸近線ですが、\(y = a^x + q\) では \(y = q\) が漸近線となります。
\(y − 2 = 3^{x − 1}\) より、
\(y = 3^x\) のグラフを \(x\) 軸方向に \(1\)、\(y\) 軸方向に \(2\) だけ平行移動したグラフである。
値域は \(y > 2\)
底 \(3\) は \(1\) より大きいので、グラフは単調増加する。
\(x = 0\) のとき \(\displaystyle y = 3^{−1} + 2 = \frac{7}{3}\)
よって、グラフは以下の通り。
答え:
\(y = 3^x\) のグラフを \(x\) 軸方向に \(1\)、\(y\) 軸方向に \(2\) だけ平行移動したグラフ

計算問題②「指数関数の最大値・最小値」
関数 \(y = 4^{x + 1} − 2^{x + 2} + 2\) \((x \leq 2)\) の最大値と最小値を求めよ。

変数の置き換えを行うと、二次関数の最大・最小問題に落とし込めます。
置き換えた変数の定義域を調べること、最後は \(x\) について解くことを忘れないようにしましょう。
\(2^x = t\) とおくと、\(t > 0\)
\(x \leq 2\) より \(0 < t \leq 4\) …①
\(\begin{align} y &= 4^{x + 1} − 2^{x + 2} + 2 \\ &= 4 \cdot 4^x − 4 \cdot 2^x + 2 \\ &= 4(2^x)^2 − 4 \cdot 2^x + 2 \\ &= 4t^2 − 4t + 2 \\ &= 4 \left( t − \frac{1}{2} \right)^2 + 1 \end{align}\)

①の範囲において、\(y\) は \(t = 4\) で最大、\(\displaystyle t = \frac{1}{2}\) で最小となる。
\(t = 4\) のとき \(2^x = 4\)、すなわち \(x = 2\)
\(\displaystyle t = \frac{1}{2}\) のとき \(\displaystyle 2^x = \frac{1}{2}\)、すなわち \(x = −1\)
したがって、\(y\) は
\(x = 2\) のとき最大値 \(50\)、\(x = −1\) のとき最小値 \(1\) をとる。
答え:
\(x = 2\) のとき最大値 \(50\)、\(x = −1\) のとき最小値 \(1\)
指数方程式の解き方【例題】
指数方程式(指数関数を含む方程式)の解き方を以下の例題を通して説明します。
方程式 \(4^x − 2^{x + 2} − 32 = 0\) を解け。
まずは、同じ底をもつべき乗で統一されるように式を整理します。
\(4^x − 2^{x + 2} − 32 = 0\) より
\((2^x)^2 − 4 \cdot 2^x − 32 = 0\)
\(2^x = X\) と変数を置き換えてあげると、\(X\) の二次方程式と見ることができます。
このとき、変数 \(X\) のとりうる値の範囲は必ず確認します。
\(2^x = X\) とおくと、\(X > 0\)
方程式 \((2^x)^2 − 4 \cdot 2^x − 32 = 0\) は
\(X^2 − 4X − 32 = 0\) と書き換えられる。
置き換えた変数について、方程式を解きます。
\(X^2 − 4X − 32 = 0\) より
\((X + 4)(X − 8) = 0\)
\(X > 0\) より、\(X = 8\)
変数 \(X\) の値がわかったら、元のべき乗に戻して \(x\) を求めます。
その際、指数関数の以下の性質を利用します。
指数関数の性質
\(a > 0, a \neq 1\) のとき、
\(\begin{align}\color{red}{a^p = a^q \iff p = q}\end{align}\)
つまり、方程式の左辺と右辺の指数の底がそろっていれば、指数部分は等しいといえますね。
\(X = 8\) より、\(2^x = 8\)
すなわち \(2^x = 2^3\)
よって \(x = 3\)
答え: \(\color{red}{x = 3}\)
\(4^x − 2^{x + 2} − 32 = 0\) より
\((2^x)^2 − 4 \cdot 2^x − 32 = 0\)
\(2^x = X\) とおくと、\(X > 0\)
方程式 \((2^x)^2 − 4 \cdot 2^x − 32 = 0\) は
\(X^2 − 4X − 32 = 0\) と書き換えられる。
\(X^2 − 4X − 32 = 0\) より
\((X + 4)(X − 8) = 0\)
\(X > 0\) より、\(X = 8\)
\(X = 8\) より、\(2^x = 8\)
すなわち \(2^x = 2^3\)
よって \(x = 3\)
答え: \(\color{red}{x = 3}\)
指数不等式の解き方【例題】
指数不等式(指数関数を含む不等式)の解き方を以下の例題を通して説明します。
不等式 \(\displaystyle \left( \frac{1}{4} \right)^x − 9 \left( \frac{1}{2} \right)^{x − 1} + 32 \leq 0\) を解け。
途中までは指数方程式と同様の流れです。最後に、指数の大小関係を考えます。
まずは同じ底をもつべき乗で統一されるように式を整理します。
\(\displaystyle \left( \frac{1}{4} \right)^x − 9 \left( \frac{1}{2} \right)^{x − 1} + 32 \leq 0\) より
\(\displaystyle \left\{ \left( \frac{1}{2} \right)^x \right\}^2 − 18 \left( \frac{1}{2} \right)^x + 32 \leq 0\)
\(\displaystyle \left( \frac{1}{2} \right)^x = X\) と変数を置き換えてあげると、\(X\) の二次不等式と見ることができます。
このとき、変数 \(X\) のとりうる値の範囲は必ず確認します。
\(\displaystyle \left( \frac{1}{2} \right)^x = X\) とおくと、\(X > 0\)
不等式 \(\displaystyle \left\{ \left( \frac{1}{2} \right)^x \right\}^2 − 18 \left( \frac{1}{2} \right)^x + 32 \leq 0\) は
\(X^2 − 18X + 32 \leq 0\) と書き換えられる。
置き換えた変数について、不等式を解きます。
\(X^2 − 18X + 32 \leq 0\) より、
\((X − 2)(X − 16) \leq 0\)
よって \(2 \leq X \leq 16\)
変数を元のべき乗に戻して \(x\) の値の範囲を求めます。
その際、指数関数の以下の性質を利用します。
指数関数の性質
- \(a > 1\) のとき、 \(\begin{align}\color{red}{a^p < a^q \iff p < q}\end{align}\)
- \(0 < a < 1\) のとき、 \(\begin{align}\color{red}{a^p > a^q \iff p < q}\end{align}\)
\(a > 1\) のときは不等式と指数部分の大小関係が一致しますが、\(0 < a < 1\) のときは大小関係が入れ替わることに注意しましょう。
\(2 \leq X \leq 16\) より
\(\displaystyle 2 \leq \left( \frac{1}{2} \right)^x \leq 16\)
\(2^1 \leq 2^{−x} \leq 2^4\)
底 \(2\) は \(1\) より大きいから
\(1 \leq −x \leq 4\)
各辺に \(−1\) をかけて
\(−4 \leq x \leq −1\)
答え: \(\color{red}{−4 \leq x \leq −1}\)
なお、最後の部分で底を \(\displaystyle \frac{1}{2}\) に統一しても構いません。
\(\displaystyle 2 \leq \left( \frac{1}{2} \right)^x \leq 16\) より \(\displaystyle \left( \frac{1}{2} \right)^{−1} \leq \left( \frac{1}{2} \right)^x \leq \left( \frac{1}{2} \right)^{−4}\)
底 \(\displaystyle \frac{1}{2}\) は \(1\) より小さいから
\(\color{red}{−4 \leq x \leq −1}\)
\(\displaystyle \left( \frac{1}{4} \right)^x − 9 \left( \frac{1}{2} \right)^{x − 1} + 32 \leq 0\) より
\(\displaystyle \left\{ \left( \frac{1}{2} \right)^x \right\}^2 − 18 \left( \frac{1}{2} \right)^x + 32 \leq 0\)
\(\displaystyle \left( \frac{1}{2} \right)^x = X\) とおくと、\(X > 0\)
不等式 \(\displaystyle \left\{ \left( \frac{1}{2} \right)^x \right\}^2 − 18 \left( \frac{1}{2} \right)^x + 32 \leq 0\) は
\(X^2 − 18X + 32 \leq 0\) と書き換えられる。
\(X^2 − 18X + 32 \leq 0\) より、
\((X − 2)(X − 16) \leq 0\)
よって \(2 \leq X \leq 16\)
\(2 \leq X \leq 16\) より
\(\displaystyle 2 \leq \left( \frac{1}{2} \right)^x \leq 16\)
\(2^1 \leq 2^{−x} \leq 2^4\)
底 \(2\) は \(1\) より大きいから
\(1 \leq −x \leq 4\)
各辺に \(−1\) をかけて
\(−4 \leq x \leq −1\)
答え: \(\color{red}{−4 \leq x \leq −1}\)
指数関数の微分公式
指数関数の微分公式は次のとおりです。
\(a > 0\), \(a \neq 1\) のとき、
- \(\color{red}{(a^x)’ = a^x \log a}\)
- \(\color{red}{(e^x)’ = e^x}\)
微分公式の証明は以下の記事で説明しています。
 微分公式の証明一覧!導関数の定義どおりの導出を解説
微分公式の証明一覧!導関数の定義どおりの導出を解説
\(e\) は自然対数の底で、「ネイピア数」とも呼ばれます。
 自然対数 ln、自然対数の底 e とは?定義や微分積分公式
自然対数 ln、自然対数の底 e とは?定義や微分積分公式
例題「指数関数を微分する」
次の例題を通して、指数関数の微分のやり方を説明します。
次の関数を微分せよ。
(1) \(y = 2^x\)
(2) \(y = e^{2x + 1}\)
(1) は公式 \((a^x)’ = a^x \log a\) に当てはめるだけですね。
(2) は \(y = e^u\) と \(u = 2x + 1\) の合成関数なので、合成関数の微分公式 \(\displaystyle \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\) に従います(数III)。
(1) \(y’ = \color{red}{2^x \log 2}\)
(2) \(y’ = e^{2x + 1} \cdot (2x + 1)’ = \color{red}{2e^{2x + 1}}\)
指数関数の積分公式
指数関数の積分公式は次のとおりです。
積分定数を \(C\) とおくと、\(a > 0\), \(a \neq 1\) のとき
- \(\color{red}{\displaystyle \int a^x dx = \frac{a^x}{\log a} + C}\)
- \(\color{red}{\displaystyle \int e^x dx = e^x + C}\)
ネイピア数 \(e\) のべき乗は、微分・積分してもかたちが変わりません。
例題「指数関数を積分する」
次の例題を通して、指数関数の積分のやり方を説明します。
次の不定積分を求めよ。
\(\displaystyle \int 2^x dx\)
公式 \(\displaystyle \int a^x dx = \frac{a^x}{\log a} + C\) に当てはめます。
\(\displaystyle \int 2^x dx = \color{red}{\frac{2^x}{\log 2} + C}\)(\(\color{red}{C}\) は積分定数)
一般に、例題ほど単純な問題が出ることは少なく、他の種類の関数(多項式、三角関数など)との合成関数のかたちでよく出題されます。
その際には、「置換積分法」や「部分積分法」などのテクニックが必要です。
以上で解説は終わりです!
指数の計算や指数関数は数I, II, III とずっとついて回るので、苦手なままだとかなり困ります。
指数関数の性質や問題を解くコツをつかんで、ぜひマスターしてくださいね!






